Решение ОДУ n-го порядка
Методы, рассмотренные выше, позволяют найти численное решение ОДУ только первого порядка. Однако они применимы и к уравнениям n-го порядка. Для этого ОДУn-го порядка предварительно приводится к системе n уравнений первого порядка.
Пусть, например, требуется решить ОДУвторого порядка
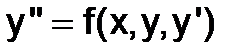 ,
,
с начальными условиями 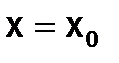 ,
, 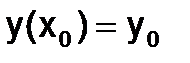 ,
, 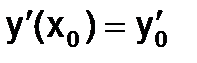 .
.
Обозначим  z=y’. В результате подстановки в исходное уравнение получим систему двух уравнений первого порядка
z=y’. В результате подстановки в исходное уравнение получим систему двух уравнений первого порядка
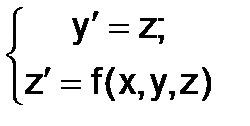 ,
,
с двумя неизвестными функциями 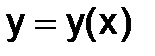 и
и 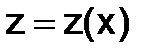 и начальными условиями
и начальными условиями
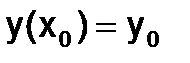 ,
, 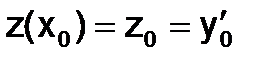 .
.
В общем виде система уравнений может быть представлена в виде
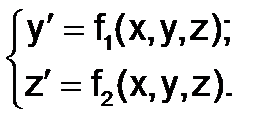 (1.5.4-1)
(1.5.4-1)
Решением системы(1.5.4-1) являются две функции 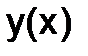 и
и 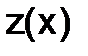 , из которых
, из которых 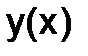 - решение исходного уравнения второго порядка. Выбрав, например, метод Эйлера, приближенное решение системы (1.5.4-1) можно найти с помощью двух рекуррентных формул:
- решение исходного уравнения второго порядка. Выбрав, например, метод Эйлера, приближенное решение системы (1.5.4-1) можно найти с помощью двух рекуррентных формул:
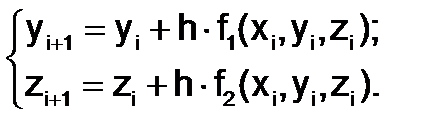
Пример 1.5.4-1. Дано обыкновенное дифференциальное уравнение второго порядка  при начальных условиях
при начальных условиях 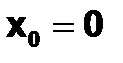 ,
, 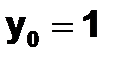 ,
, 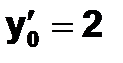 на отрезке [0;0.4] с шагом
на отрезке [0;0.4] с шагом 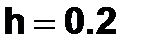 .
.
Обозначим 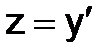 , тогда ОДУ второго порядка можно записать в виде системы ОДУ первого порядка
, тогда ОДУ второго порядка можно записать в виде системы ОДУ первого порядка
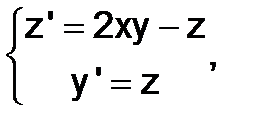 с начальными условиями
с начальными условиями 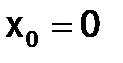 ,
, 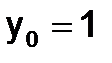 ,
, 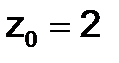 .
.
Применим метод Эйлера для решения системы ОДУ
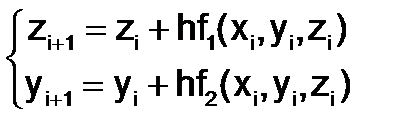
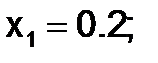
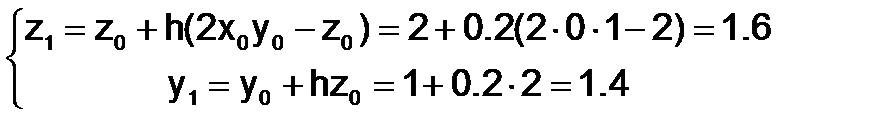
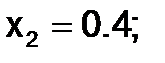
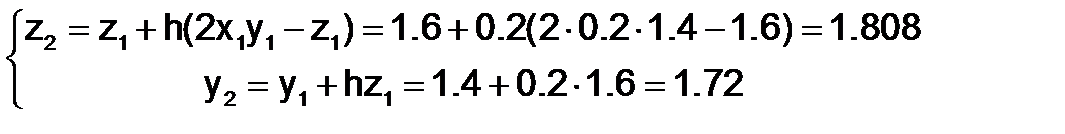
и т.д.
| xi | yi | zi |
| 0.2 | 1.4 | 1.6 |
| 0.4 | 1.72 | 1.808 |
В общем виде ОДУn-го порядка
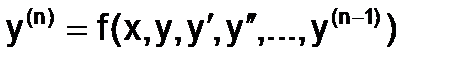 .
.
Введемследующие обозначения:
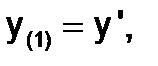
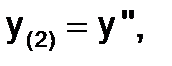 …
… 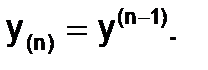
В результате этих подстановок перейдемк системеnОДУ первого порядка:
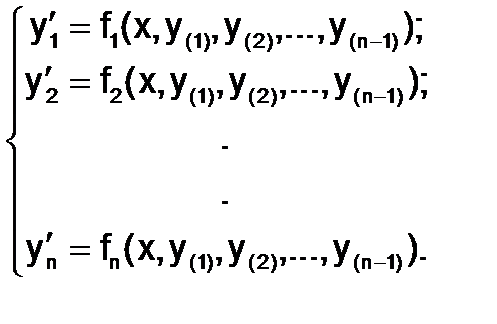 (1.5.4-2)
(1.5.4-2)
Решением системы (1.5.4-2) являются функции 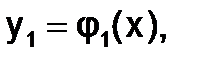
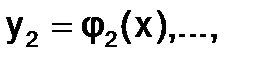
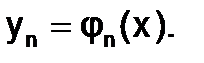
При заданных начальных условиях 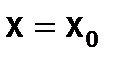 ,
, 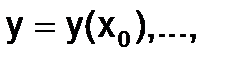
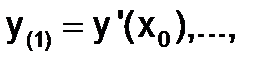
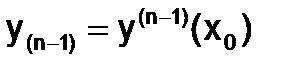 и использовании метода Эйлера решение может быть получено с помощью рекуррентных формул
и использовании метода Эйлера решение может быть получено с помощью рекуррентных формул
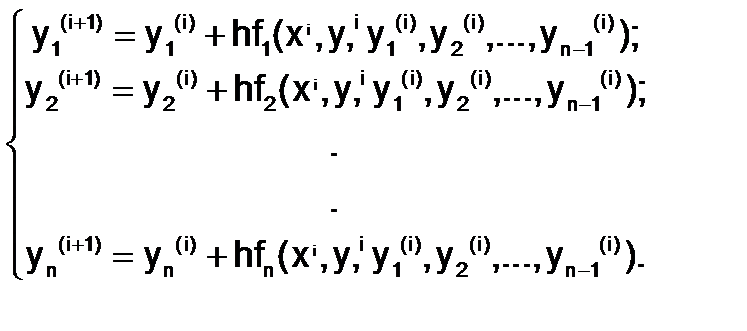
Окончательным решением ОДУn-го порядка, согласно определению, служит функция 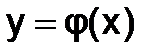 , вычисленная на заданном множестве точек[a;b].
, вычисленная на заданном множестве точек[a;b].
Дата добавления: 2016-05-31; просмотров: 1833;










