Итерационное уточнение корней.

На этапе отделения корней решается задача отыскания возможно более узких отрезков 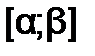, в которых содержится один и только один корень уравнения.

Этап уточнения корня имеет своей целью вычисление приближенного значения корня с заданной точностью. При этом применяются итерационные методы вычисления последовательных приближений к корню: x₀, x₁, ..., x_n, …,в которых каждое последующее приближение x_n+1вычисляется на основании предыдущего x_n. Каждый шаг называется итерацией. Если последовательность x₀, x₁, ..., x_n, …при n®¥ имеет предел, равный значению корня 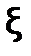, то говорят, что итерационный процесс сходится.

Существуют различные способы отделения и уточнения корней, которые мы рассмотрим ниже.

Отделение корней

Корень 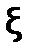уравнения f(x)=0считается отделенным (локализованным) на отрезке 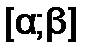, если на этом отрезке данное уравнение не имеет других корней. Чтобы отделить корни уравнения, необходимо разбить область допустимых значений функции f(x) на достаточно узкие отрезки, в каждом их которых содержится только один корень. Существуют графический и аналитический способы отделения корней.