Итерационное решение задачи

Постановка задачи

Будем считать, что на рынке одного товара функция спроса D(t) и функция предложения S(t) – линейные функции цены Р(t) на момент времени t или цены Р(t –1) предыдущего момента времени.

Функция спроса:

D(t) = a + A 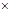P(t), (7-1)

где a, А – постоянные параметры.

Функция предложения:

S(t) = b + B 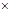P(t –1), (7-2)

где b, В – постоянные параметры.

Если приравнять формулы (7-1) и (7-2), получим условия стабильности процесса – линейное уравнение, где цена выступает в качестве переменной :

P(t) = (B/A) 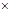P(t – 1) + (b – a /A) (7-3)

Цена равновесия Р*, при которой Р(t) = P(t – 1), согласно приведенной выше формуле равна:

P* = (b – a) / (A – B), (7-4)

и, следовательно, условием, определяющим P(t) ® P* при t ® ¥ , служат неравенства:

-1 < В/А < 1 ; В/А < 1. (7-5)

Подтверждением условия того, что процесс сошелся, будем считать выполнение условия P(t) – P(t – 1) < e для некоторого достаточно малого положительного значения e.0

Вычислительная процедура базируется на использовании программы итеративных вычислений BASIC 4. Чтобы получить наглядный результат, рекомендуется ввести в программу следующие значения А и В:

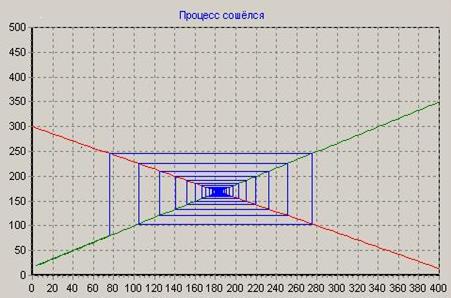
Вариант 1: случай сходимости А = 1,4 ; В = 1,2 ; Р(0) = 80

При А > В, рыночная цена, движущаяся попеременно то вверх, то вниз по направлению против часовой стрелки, вычерчивает соответствующаю этому циклу ломаную. В результате Р(0) достигает величины равновесия – Р*. Нужно отметить, что колебания рыночных цен и количества сделок движутся последовательно. Так как, после увеличения цен, незамедлительно вырастает количество сделок и наоборот.