Оценка вероятности промаха БП типа кэш.

Будем выяснять вероятность «промаха» в зависимости от параметров кэш-памяти.

Пусть способ отображения БП - группо-ассоциативный. Введем параметр ассоциативности S, который показывает сколько областей в БП. V-объем БП (в блоках), n-число ячеек в блоке.

1) Пусть рабочая нагрузка состоит из операторов следования. Пусть К- объем программы в блоках.

Вероятность «промаха»:

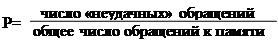
При обращении к кэш-памяти за очередной командой происходит «промах» только для первой команды, принадлежащей данному блоку, т.к. в блок БП переписывается не только эта команда, но и остальные, следовательно происходит процесс опережающего ввода.

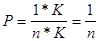
Вывод: чем больше ячеек в блоке - тем меньше вероятность «промаха».

2) Пусть программа состоит из команд следования и перехода вперед.

Пусть q_i - вероятность того, что после выполнения текущей команды должна выполняться команда, отстоящая от текущей на i адресов вперед.

Пусть выполнилась первая команда, принадлежащая данному блоку, тогда вероятность того, что этот блок обеспечит выполнения только одной команды равна:

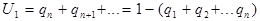
две команды:

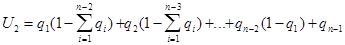
ДЗ. Найти U₃ и вывести рекуррентное соотношение.

Найдем среднее число команд, которые дает блок:

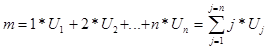
ДЗ. Найти m, если q_i=1/n (если n®¥, то можно убедится, что m=e=2,47...)

Вероятность «промаха»:

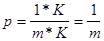
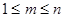
Вывод: команды ветвления вперед увеличивают вероятность «промаха».

3) Программа состоит из всех трех операторов. Пусть длина цикла составляет l блоков и число повторений - r. При определении вероятности «промаха» рассмотрим три случая:

1. l £ V

2. V+V/S £ l

3. V £ l £ V+V/S

Рассмотрим первый случай (l £ V).

Этот случай характерен тем, что на первом цикле (шаге) (всего r) в БП нет ни одного блока программы, следовательно, при обращении к каждому блоку программы будет, происходит один «промах». На остальных циклах промахов нет. Для простоты будем считать, что программа начинается с начала области.

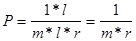
Рассмотрим второй случай (V+V/S £ l)

Пусть будет алгоритм замещения LRU.

На первом цикле при обращении к первым V блокам программы будет происходить один «промах», а V+1 блок вытесняет первый блок БП и т.д. На втором цикле тоже происходят вытеснения. Действительно первый блок программы отсутствует в БП (вместо него V+1 блок) следовательно, произойдет вытеснение V/S+1 блока и т.д.

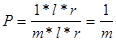
Рассмотрим третий случай (V £ l £ V+V/S).

На первом цикле при обращении к первым V блокам программы будет происходить один «промах», а хвост программы (l-V блоков) вытесняет первые блоки из БП. На остальных циклах вытеснения происходят только с первыми l-V блоками каждой области БП.

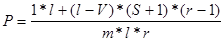
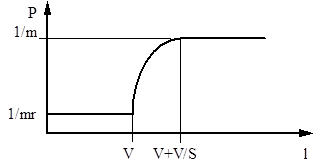
На рис. приведена зависимость вероятности «промаха» от длины программы, состоящей из операторов следования, ветвления и цикла.

Пусть нам зафиксировали объем КЭШа и наша задача - найти параметр ассоциативности S (1£ S £.V). Если S=V, то мы имеем чисто ассоциативное отображение. Если S=1, то второй участок зависимости наиболее пологий, следовательно, мы имеем оптимальное значение параметра ассоциативности, принимая во внимание только «промах» при обращении к БП типа кэш (вероятность «промаха»).

Лекция №3