Множительные структуры коробок скоростей

Закономерность геометрического ряда частот вращения шпинделя позволяет проектировать коробки скоростей наиболее простой структуры, состоящей из элементарных двухваловых механизмов, последовательно соединенных между собой в одну или несколько кинематических цепей. Такая структура называется множительной, так как кинематические условия настройки этих приводов определяются свойствами множительных групп передачи, а общее число скоростей получается перемножением чисел скоростей элементарных двухваловых передач [6].

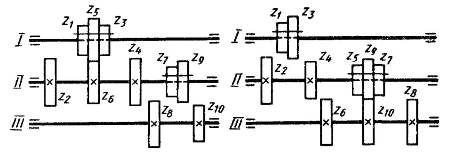
Рассмотрим устройство шестиступенчатой коробки скоростей (рис. 3.1, а). Для передачи вращения от вала I валу II служит множительный механизм с трехвенцовым блоком, а от вала II валу III – с двухвенцовым блоком. В результате последовательного соединения этих элементарных механизмов при одной скорости ведущего вала I ведомый вал III (или шпиндель) может иметь шесть различных скоростей.

Рис. 3.1.Кинематическая схема шестиступенчатой коробки скоростей

Совокупность передач, связывающих вращение двух соседних валов, образует группу передач. Ее характеризуют два показателя: количество передач в группе р и величины их передаточных отношений i.

В рассматриваемой схеме даны две множительные группы: первая состоит из трех передач (z₁ – z₂, z₃ – z₄, z₅ – z₆), вторая – из двух (z₇ – z₈, z₉ – z₁₀). Порядок чередования групп вдоль кинематической цепи характеризует конструктивный вариант коробки. Его условно можно выразить в виде структурной формулы: z_n = 6 = 3 × 2.

На рис. 3.1, б представлена схема шестиступенчатой коробки скоростей, имеющей другой конструктивный вариант (порядок). Здесь в первой группе две передачи (z₁ – z₂, z₃ – z₄), a во второй группе – три (z₅ – z₆, z₇ – z₈, z₉ – z₁₀).

Структурная формула для этого варианта z_n = 6 = 2 · 3. В общем виде число ступеней скорости

,

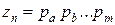где р_а, р_b, …, p_m – число передач в первой, второй, …, m-й группах.

Количество конструктивных вариантов одной и той же структуры равно числу перестановок m групп, т.е.

,

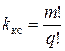где q – число групп с одинаковым количеством передач.

Для нашего случая т = 2, q = 1, следовательно, 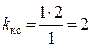, а z_n = 6 = 3 · 2 = 2 · 3. Если принять число передач в группах 2 и 3, то для 12-ступенчатой коробки z_n = 12 = 3·2·2 = 2·3·2 = 2·2·3. Так как т = 3, q = 2, то число конструктивных вариантов .

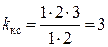Передаточные отношения зависят от так называемой характеристики группы, обусловленной кинематическим порядком (вариантом) включения передач при переходе от одной частоты вращения шпинделя к другой.

Вернемся к рис. 3.1, а. Примем порядок включения: используем все три положения блока z₂ – z₄ – z₆ сначала при левом положении шестерен z₇ – z₉, а затем при правом положении. Если п – частота вращения вала I, то ряд чисел оборотов вала IIIможно выразить следующими равенствами:

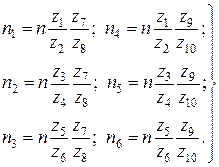
При последовательном переключении колес первой группы частота вращения вала III изменяется в φ раз. Переключение колес второй группы (c n₁ на n₄, c n₂ на n₅ или с n₃ на n₆) дает увеличение частоты вращения в φ³ раз. В общем случае при переключении передач в какой-либо группе частота вращения выходного вала (шпинделя) изменяется в φ^x раз. Показатель степени х называется характеристикой множительной группы передач. Для принятого нами кинематического порядка характеристика первой группы передач x₁ = 1, а второй х₂ = 3. Структурную формулу, уточняющую не только конструктивный, но и кинематический порядок, принято записывать так:

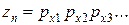
Здесь место группы в формуле показывает конструктивный порядок и номер группы, а индекс – ее характеристику. Для нашего примера z_n = 6 = 3₁2₃. Такая запись означает, что первая группа имеет три передачи, а ее характеристика x₁ = 1; вторая группа – две передачи, а ее характеристика х₂ = 3. Группу передач, имеющую характеристику х = 1, называют основной группой, остальные группы (с х >1) – переборными. Величина х в общем случае не может быть произвольной, за исключением случаев, когда мы искусственно изменяем характеристику. Если первая группа является основной, то характеристика последующих групп равна числу ступеней скорости совокупности групповых передач, кинематически предшествующих данной группе. Это положение представляется в следующем виде. Если x₁ = 1, то х₂ = p_a, х₃ = р_a p_b…, х_m = р_a p_b…p_m-1, например, z_n = 8 = 2₁2₂2₄; z_n = 12 = 3₁2₃2₆; z_n = 18 = 3₁3₃2₉. Возможны и другие кинематические варианты, например, z_n = 12 = 3₁2₆2₃ = 2₃3₁2₆ = 2₆3₁2₃ = 2₃2₆3₁ = 2₆2₃3₁. Общее их количество равно числу перестановок из m элементов, т.е. 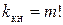. Для рассматриваемого случая (z_n = 6) k_кн = 1·2 = 2. Общее количество возможных вариантов (конструктивных и кинематических) для обычных множительных структур

.

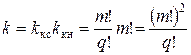Для шестиступенчатой коробки скоростей (см. рис. 3.1) m = 2, q = 1, 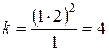, а варианты: z_n = 6 = 3₁2₃= 2₃3₁ = 2₁3₂ = 3₂2₁.

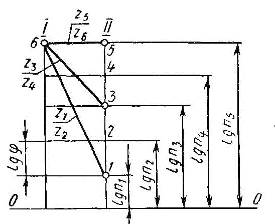
Графическое изображение множительной структуры основано на условном графическом изображении валов и передач. Проведем две вертикальных линии I и II (рис. 3.2, а). Отложим от линии 00 отрезки, равные lg n₁, lg n₂, lg n₃... Через точки 1, 2, 3, ... проведем горизонтальные линии. Вертикали I и II условно изображают валы, а точки 1, 2, 3, ... – их угловые скорости. Число точек на вертикальной линии указывает на количество угловых скоростей данного вала. Отрезки 1 – 2, 2 – 3, 3 – 4, … равны lg φ.

а)	б)

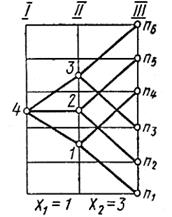
Рис. 3.2. Графическое изображение множительной структуры

Передачи условно изображают прямыми линиями – лучами (например, 6 – 5, 6 – 3, 6 – 1). Концы лучей соединяют с точками, соответствующими частотам вращения ведущего и ведомого валов. Луч 6 – I, например, изображает зубчатую передачу. Колесо с z₁ вращается с валом I со скоростью n₅, а колесо с z₂ вращается с валом II cо скоростью n₁.

Лучи с наклоном вверх (считая слева направо) изображают ускорительную передачу, а направленные вниз – замедляющую (редуцирующую) передачу. Передаточное отношение передачи i = φ ± S_x, где S_x – число интервалов (lg φ), на которое поднимается или опускается луч, изображающий передачу. Для ускорительной передачи s имеет положительное значение, для замедлительной – отрицательное. Пусть лучи 6 – 1, 6 – 3 и 6 – 5 (рис. 3.2, а) изображают для примера группу передач с трехвенцовым блоком (например, z₁ – z₂, z₃ – z₄, z₅ – z₆, рис. 3.1, а).