В исходной системе координат

Деформированное состояние в точке также является тензором, составляющие которого являются линейными и угловыми деформациями.

Составляющие тензора деформаций можно найти из закона Гука для объемного напряженного состояния по заданному тензору напряжений. Определим сначала модуль упругости при сдвиге:

.

Из закона Гука деформации в заданной точке по координатным осям и координатным площадкам (по ребрам и граням выделенного элементарного параллелепипеда) равны:

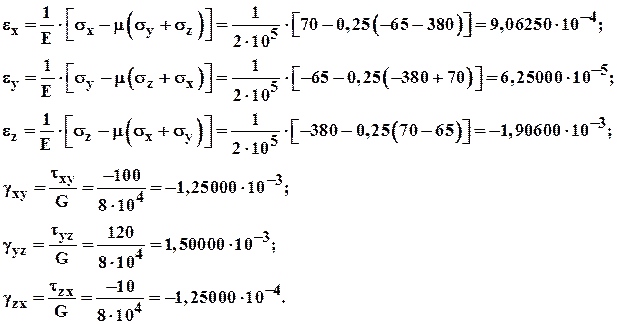
Здесь деформации вычислялись до пятого знака после запятой для того, чтобы при вычислении инвариантов деформированного состояния не возникли бы существенные ошибки, особенно при вычислении определителя в третьем инварианте .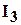

Таким образом, тензор деформированного состояния имеет вид:

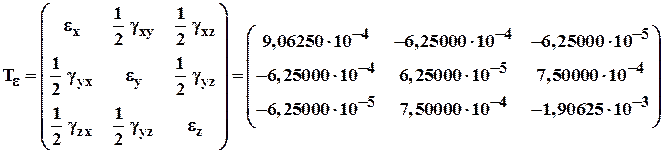
В качестве составляющих тензора напряжений записываются не полные касательные напряжения, а их половинные значения для того, чтобы матрица, изображающая тензор деформаций, была симметричной.

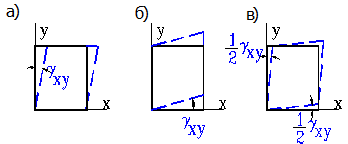
Рис. 2.4. Разные представления сдвиговых деформаций в плоскости XOY

Кроме этого такое представление тензора деформаций наглядно демонстрирует закон парности касательных напряжений.