Определение напряжений и деформаций по заданному тензору напряжений

При выполнении контрольной работы студенты должны понять, что напряжения, возникающие в точках нагруженного тела, зависят не только от величины нагрузки, но и от ориентации площадки, где они действуют. Площадкой называют бесконечно малую часть сечения, располагающуюся около рассматриваемой точки. По разным площадкам, проведенным через точку, действуют разные напряжения, причем каждое напряжение является не самостоятельным объектом, а составляющим объекта, который называется напряженное состояние в точке.

Напряженным состоянием в точке нагруженного тела называется совокупность напряжений, действующих по всем площадкам, проведенным через эту точку. Для оценки прочности тела в любой точке необходимо знать именно напряженное состояние в этой точке, а не напряжение по какой-либо площадке. Исследуя напряженное состояние тела в данной точке, вводят систему координат с центром в этой точке и около нее координатными площадками выделяют элементарный параллелепипед. К граням параллелепипеда прикладывают напряжения, заменяющие воздействие удаленной части тела.

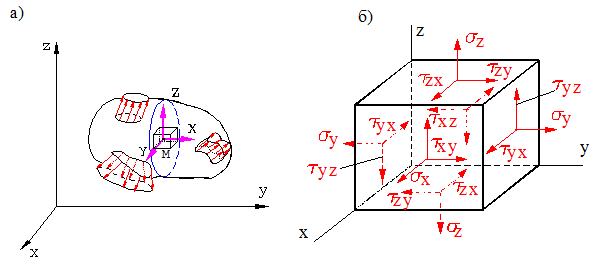
Рис. 0.1. Напряженное состояние в точке

Для определения напряжений, действующих по выбранной площадке, нужно сначала ориентировать эту площадку в системе координат. Такая ориентация выполняется с помощью нормали к этой площадке, а положение нормали в выбранной системе координат определяется с помощью трех направляющих косинусов (в трехмерном пространстве).

Направляющим косинусом нормали называется косинус угла, составленного нормалью к площадке и одной из координатных осей.

Напряженное (как и деформированное) состояние в точке является тензорным объектом. Все его свойства (как, например, существование инвариантов напряжений, главных напряжений и др.) обусловлены не спецификой напряженного или деформированного состояния, а спецификой симметричного тензора второго ранга. Если известен тензор напряжений, то можно вычислить напряжения на любой площадке, проведенной через данную точку.

Тензор является более сложным понятием, чем вектор и скаляр. Ему можно дать следующее определение:

тензором называется физический или математический объект, составляющие которого преобразуются по закону, действующему для произведений координат векторов [4].

Тензор представляется матрицей, элементами которой являются напряжения, действующие по граням элементарного параллелепипеда, выделенного около рассматриваемой точки (см. рис. 1.1):

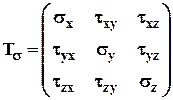. (0.1)

Рис. 0.2. Тензор напряжений

Индексы у нормальных напряжений соответствуют нормалям к площадкам, по которым действуют эти напряжения. Касательные напряжения обозначаются с двумя индексами: первый индекс соответствует нормали к площадке, по которой действует напряжение, а второй – оси, параллельно которой оно действует.

Правило знаков для напряжений формулируется следующим образом.

Напряжение, действующее по площадке с положительной внешней нормалью, считается положительным, если оно направлено в положительную сторону параллельной ему оси.

В противном случае напряжение считается отрицательным. Например, для площадки с отрицательной внешней нормалью правило знаков можно переформулировать так:

Напряжение, действующее по площадке с отрицательной внешней нормалью, считается положительным, если оно направлено в отрицательную сторону параллельной ему оси.

Это общее правило не противоречит правилу знаков для нормальных напряжений, изучаемое в сопротивлении материалов:

нормальное напряжение считается положительным, если оно вызывает растяжение.

Элементарный параллелепипед выделяется так, чтобы его ребра совпадали с координатными осями (которые могут быть выбраны как угодно). Так как напряжения зависят от положения площадки (грани параллелепипеда), а ориентация параллелепипеда зависит от выбора системы координат, то в разных системах координат составляющие тензора напряжений (напряжения) будут разными. Физический же объект «напряженное состояние в точке» от выбора системы координат не зависит. Следовательно, одно и то же напряженное состояние может быть представлено разными матрицами. Однако, эти матрицы должны иметь «что-то общее», т. к. они описывают один и тот же физический объект. Это «общее» является инвариантами напряженного состояния. Из математики известно, что инвариантом называется величина, не зависящая от системы координат. В теории упругости (и в полных курсах «Сопротивление материалов») доказывается, что инварианты напряженного состояния имеют вид:

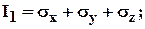
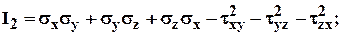(0.2)

.

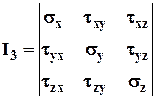Рис. 0.3. Инварианты напряженного состояния

Тензорное исчисление возникло в средине XIX века в связи с решением задач теории упругости для того, чтобы компактно записывать громоздкие преобразования объектов (напряжений, деформаций) при переходе от одной системы координат к другой. Однако широкое применение оно получило лишь в XX в. Например, А. Эйнштейн свою диссертацию по теории относительности написал в тензорной форме.

Тензорное исчисление излагается в многочисленной математической и специальной научной литературе. Познакомиться с ним можно, например, в книгах [2], [3], [4], [5].