Работа газовых изопроцессов

Пусть газ заключен в цилиндрический сосуд, закрытый плотно пригнанным и легко скользящим поршнем (рис.10.3). При расширении газ будет совершать работу DA = FDh , где F - сила, с которой газ действует на площадь поршня S; Dh - перемещение поршня при расширении газа. Приращение объема газа DV = SDh . Подставляя силу F = pS и DV в выражение для работы, получим DA = pDV . При расширении газа работа будет положительной, при сжатии - отрицательной. Если давление газа при совершении работы изменяется, то находят работу при каждом элементарном изменении объема

dA = pdV (10.4)

суммируют все элементарные работы для этого газового процесса. Полная работа

A = 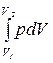, (10.5)

где V₁ - начальный объем газа, V₂ - его конечный объем. Применим формулу (10.5) для расчета работы изопроцессов.

1. Рассмотрим изохорический процесс. Для этого процесса объем газа V = const , dV = 0 и A = 0 . Газ не совершает работу. Первое начало термодинамики (10.3) будет иметь вид DQ = DU , т.е. все тепло, сообщенное газу, пойдет на его нагревание.

2. Рассмотрим изобарический процесс. Так как давление не изменяется, то его как постоянную величину можно вынести из под знака интеграла (10.5). Получим A = p(V₂ - V₁) или с учетом уравнения Менделеева-Клапейрона pV = (m /m)RT , записанного для начального и конечного состояний, получим выражение для работы изобарического процесса

A = (m /m)R(T₂ - T₁). (10.6)

3. Рассмотрим изотермический процесс. Так как температура постоянна, то внутренняя энергия идеального газа не изменяется: DU = 0 . Первое начало термодинамики (10.3) будет иметь вид DQ = DA, т.е. все тепло, подведенное к системе, будет затрачено на совершение ею работы. Используя уравнение состояния идеального газа (10.6) и учтя, что T = const , запишем выражение (10.5) для работы изотермического процесса в виде

A = 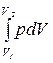= (m /m)RT 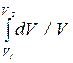= (m /m)RT ln(V₂ /V₁). (10.7)