Момент импульса тела относительно оси равен произведению момента инерции тела относительно оси на угловую скорость вращения тела относительно этой оси.
Уравнение динамики тела, вращающегося вокруг неподвижной оси OZ, имеет вид:
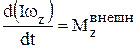 .
.
Если тело в процессе вращения не деформируется то его момент инерции 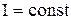 , и уравнение динамики вращательного движения тела относительно оси преобразуется к виду
, и уравнение динамики вращательного движения тела относительно оси преобразуется к виду
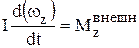 .
.
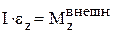 ,
,
где 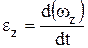 – проекция вектора углового ускорения на ось вращения.
– проекция вектора углового ускорения на ось вращения.
Угловое ускорение твёрдого тела относительно оси Z пропорционально моменту силы и обратно пропорционально моменту инерции тела
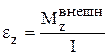 .
.
Момент инерции тела I является мерой инертности вращательного движения тела твёрдого тела.
Момент инерции твёрдого тела относительно оси в случае непрерывного распределения массы можно вычислить по формуле:
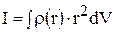 ,
,
где 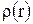 – плотность тела,
– плотность тела, 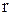 – расстояние от элементарного объёма
– расстояние от элементарного объёма 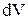 до оси вращения. В случае однородного тела
до оси вращения. В случае однородного тела 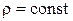 и момент инерции
и момент инерции
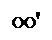
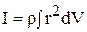 .
.
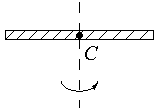
 1. Момент инерции тонкого однородного стержня относительно оси вращения ОО', перпендикулярной стержню и проходящей через его середину (рис.7),
1. Момент инерции тонкого однородного стержня относительно оси вращения ОО', перпендикулярной стержню и проходящей через его середину (рис.7), 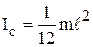 , где m – масса стержня,
, где m – масса стержня,  – длина стержня.
– длина стержня.
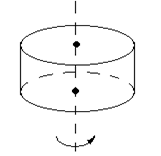
 2. Момент инерции однородного диска (цилиндра) массой m и радиусом R относительно оси вращения ОО', перпендикулярной плоскости диска и проходящей через его геометрический центр (рис.8),
2. Момент инерции однородного диска (цилиндра) массой m и радиусом R относительно оси вращения ОО', перпендикулярной плоскости диска и проходящей через его геометрический центр (рис.8), 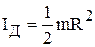 .
.



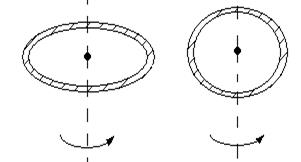
 3. Момент инерции тонкого однородного кольца массой m и радиусом R относительно оси ОО', перпендикулярной плоскости кольца и проходящей через его геометрический центр
3. Момент инерции тонкого однородного кольца массой m и радиусом R относительно оси ОО', перпендикулярной плоскости кольца и проходящей через его геометрический центр 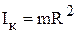 (рис.9, а); относительно оси ОО'', совпадающей с диаметром,
(рис.9, а); относительно оси ОО'', совпадающей с диаметром, 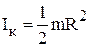 (рис.9, б).
(рис.9, б).
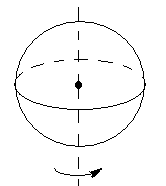 4. Момент инерции однородного шара относительно оси ОО', проходящей через его геометрический центр (рис.10),
4. Момент инерции однородного шара относительно оси ОО', проходящей через его геометрический центр (рис.10), 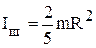 , где
, где 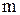 – масса шара,
– масса шара, 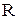 – радиус шара.
– радиус шара.

 Другие примеры значений моментов инерции тел простой геометрической формы приведены в приложении 1.
Другие примеры значений моментов инерции тел простой геометрической формы приведены в приложении 1.
Величина момента инерции тела определяется положением оси вращения. В практических задачах часто встречаются случаи, когда требуется вычислить момент инерции тела относительно произвольной оси вращения. Это можно сделать с помощью теоремы Штейнера.
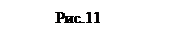 Момент инерции телаIотносительно произвольной оси АА'(рис. 11) равен сумме момента инерции тела
Момент инерции телаIотносительно произвольной оси АА'(рис. 11) равен сумме момента инерции тела 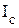 относительно оси ОО', проходящей через центр инерции и параллельной оси АА', и произведению массы тела на квадрат расстоянияdмежду осями ОО' и АА'
относительно оси ОО', проходящей через центр инерции и параллельной оси АА', и произведению массы тела на квадрат расстоянияdмежду осями ОО' и АА'
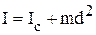 .
.
Дата добавления: 2021-02-19; просмотров: 458;











