Средняя длина свободного пробега молекул.
Вследствие хаотического теплового движения молекулы газа непрерывно сталкиваются друг с другом, проходят сложный зигзагообразный путь. Между 2-мя столкновениями молекулы движутся равномерно прямолинейно.
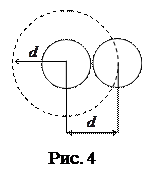 Минимальное расстояние, на которое сближаются центры 2-х молекул при соударении, называется эффективным диаметром молекулы d (рис. 4).
Минимальное расстояние, на которое сближаются центры 2-х молекул при соударении, называется эффективным диаметром молекулы d (рис. 4).
Величина 
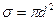 называется эффективным сечением молекулы.
называется эффективным сечением молекулы.
Найдем среднее число столкновений молекулы однородного газа в единицу времени. Столкновение произойдёт, если центры молекул сблизятся на расстояние, меньшее или равное d. Предполагаем, что молекула движется со скоростью 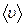 , а остальные молекулы покоятся. Тогда число столкновений определяется числом молекул, центры которых находятся в объёме, представляющем собой цилиндр с основанием
, а остальные молекулы покоятся. Тогда число столкновений определяется числом молекул, центры которых находятся в объёме, представляющем собой цилиндр с основанием 
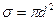 и высотой, равной пути, пройденном молекулой за 1с, т.е.
и высотой, равной пути, пройденном молекулой за 1с, т.е. 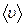 .
.
 В действительности все молекулы движутся, и возможность столкновения 2-х молекул определяет их относительная скорость. Можно показать, что если для скоростей молекул принято распределение Максвелла,
В действительности все молекулы движутся, и возможность столкновения 2-х молекул определяет их относительная скорость. Можно показать, что если для скоростей молекул принято распределение Максвелла, 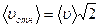 .
.
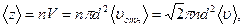
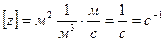 .
.
Для большинства газов при нормальных условиях
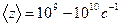 .
.
Средняя длина свободного пробега - это среднее расстояние, которое проходит молекула между двумя последовательными соударениями. Оно равно отношению пройденного за время Dt пути к числу соударений за это время:
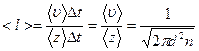
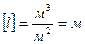
Для большинства газов при нормальных условиях 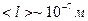 .
.
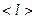 обратно пропорциональна концентрации молекул.
обратно пропорциональна концентрации молекул.
Поскольку 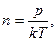
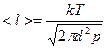
При T =const 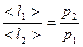 ,
, 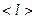 обратно пропорциональна давлению.
обратно пропорциональна давлению.
Явления переноса.
В термодинамических неравновесных системах возникают особые необратимые процессы, называемые явлениями переноса, в результате которых происходит пространственный перенос массы, количества движения, энергии. К явлениям переноса относятся диффузия, внутреннее трение, теплопроводность. В основе всех 3-х процессов лежит один механизм - хаотическое движение и перемешивание молекул, поэтому их закономерности должны быть похожи, а количественные характеристики тесно связаны друг с другом.
Нарушение равновесия приводит к возникновению пространственной неоднородности какой-либо физической величины (плотности, температуры, скорости упорядоченного движения слоёв).
Движение молекул выравнивает эти неоднородности. Каждая молекула обладает массой 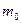 , импульсом
, импульсом 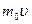 , энергией
, энергией 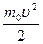 .
.
Явление переноса в газах и жидкостях состоят в том, что в этих веществах возникает упорядоченный, направленный перенос массы (диффузия), импульса (внутреннее трение), внутренней энергии (теплопроводность). При этом в газах нарушается полная хаотичность движения молекул и максвелловское распределение молекул по скоростям.
а). Диффузией называется самопроизвольное взаимное проникновение и перемещение молекул двух соприкасающихся газов, жидкостей или твердых тел.
Рассмотрим это явление вначале с макроскопической точки зрения, а затем с позиции МКТ.
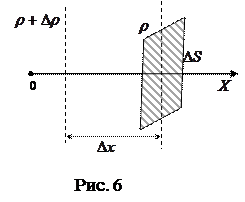 1) DS ^ оси ОХ (рис.6). Пусть в 2-х точках, отстоящих друг от друга на Dх, плотность отличается на Dr.
1) DS ^ оси ОХ (рис.6). Пусть в 2-х точках, отстоящих друг от друга на Dх, плотность отличается на Dr.
Согласно закону Фика, установленному экспериментально, масса газа DM, переносимая за время Dt через площадку DS, прямо пропорциональна величине этой площадки, времени Dt и градиенту плотности 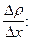
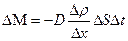 (4)
(4)
где 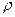 - плотность газа,
- плотность газа, 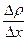 - градиент плотности, т.е. изменение плотности на единице длины в направлении наиболее быстрого её возрастания, D - коэффициент диффузии.
- градиент плотности, т.е. изменение плотности на единице длины в направлении наиболее быстрого её возрастания, D - коэффициент диффузии.
Градиент (от лат gradiens - шагающий) - мера измерения какой-либо физической величины при перемещении на единицу длины в направлении наиболее быстрого её возрастания. Если отношение 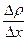 непостоянно, его следует заменить производную
непостоянно, его следует заменить производную 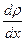 . Знак “-” показывает, что перенос массы осуществляется в направлении убывания плотности.
. Знак “-” показывает, что перенос массы осуществляется в направлении убывания плотности.
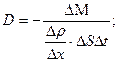
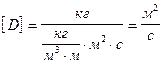 .
.
Согласно кинетической теории газов 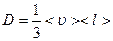 .
.
Коэффициент D - численно равен массе вещества, переносимого в единицу времени через единицу поверхности при градиенте плотности, равном единице. Величина D зависит от вида газа и условий, при которых он находится.
2) Рассмотрим явление диффузии с точки зрения МКТ.
Для простоты рассмотрим два одинаковых взаимно проникающих газа, т.е. массы молекул одинаковы. При одинаковых условиях у таких молекул одинаковы 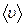 и
и 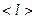 . Плоскость, которой принадлежит площадка DS, делит систему газов на две области: I и II (рис.7).
. Плоскость, которой принадлежит площадка DS, делит систему газов на две области: I и II (рис.7).
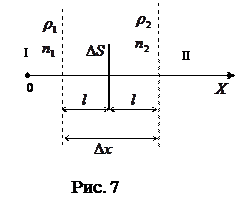 Ввиду хаотичности движения молекул считаем, что 1/3 их движется вдоль ОХ, а к площадке DS - 1/6 от общего числа молекул. За время Dt через DS из I в II перейдут N1 молекул:
Ввиду хаотичности движения молекул считаем, что 1/3 их движется вдоль ОХ, а к площадке DS - 1/6 от общего числа молекул. За время Dt через DS из I в II перейдут N1 молекул:
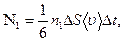
а в обратном направлении
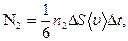
Уточним, к каким точкам областей I и II следует отнести концентрации молекул n1 и n1 . Через DS проходят молекулы только из того места, где они испытали последнее столкновение, т.е. с расстояния, равного 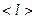 .
.
Определим разность между числом молекул N1 и N2, проходящих через DS за Dt в обоих направлениях:
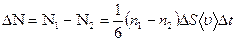 |
| 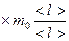
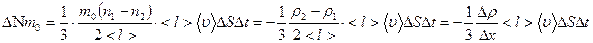 ,
,
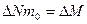 - масса газа, перешедшая через DS за Dt
- масса газа, перешедшая через DS за Dt
DM= 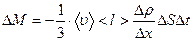 - (5)
- (5)
на основе МКТ.
(4) и (5) совпадают, если положить 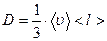 .
.
При нормальных условиях 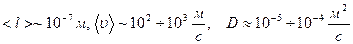 .
.
Т.к. 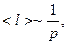 то
то 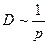 (т.к.
(т.к. 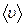 не зависит от р) - в разреженных газах диффузия идет быстрее.
не зависит от р) - в разреженных газах диффузия идет быстрее.
Т.к. 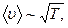 то D ~
то D ~ 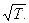
б). Внутреннее трение в газах (вязкость).
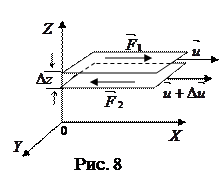 Вязкостью газов (жидкостей) называется их свойство оказывать сопротивление перемещению одних слоев относительно других. Явление вязкости связано с возникновением сил трения между слоями газа, перемещающимися параллельно друг другу с различными скоростями. Со стороны более быстрого слоя на медленный действует ускоряющая сила
Вязкостью газов (жидкостей) называется их свойство оказывать сопротивление перемещению одних слоев относительно других. Явление вязкости связано с возникновением сил трения между слоями газа, перемещающимися параллельно друг другу с различными скоростями. Со стороны более быстрого слоя на медленный действует ускоряющая сила 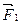 , а со стороны медленного – задерживающая
, а со стороны медленного – задерживающая 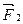 (рис. 8). Силы трения направлены по касательной к поверхности слоев и определяются эмпирической формулой:
(рис. 8). Силы трения направлены по касательной к поверхности слоев и определяются эмпирической формулой:
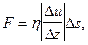 (6)
(6)
где h - динамическая вязкость, 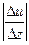 - градиент скорости, DS - площадь слоя.
- градиент скорости, DS - площадь слоя.
Формула (6) определяет модуль двух противоположно направленных сил 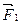 и
и 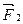 , с которыми слои действуют друг на друга, поэтому отношение
, с которыми слои действуют друг на друга, поэтому отношение 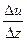 тоже берем по модулю.
тоже берем по модулю.
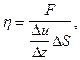
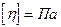 ·с=
·с= 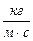
Коэффициент h численно равен силе внутреннего трения, действующей на единицу площади поверхности раздела параллельно движущимся слоям при градиенте скорости равном 1.
n= 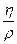 - кинематическая вязкость.
- кинематическая вязкость.
У газов с ростом температуры динамическая вязкость h растёт.
МКТ объясняет вязкость переносом импульса молекул от одного слоя другому.
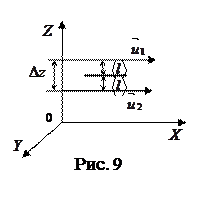 Выделим в газе два слоя, движущиеся с
Выделим в газе два слоя, движущиеся с 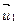 и
и 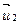 (рис. 9). Каждая молекула одновременно участвует в двух движениях:
(рис. 9). Каждая молекула одновременно участвует в двух движениях:
1).хаотическом с 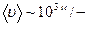 ;
;
2).упорядоченном с 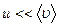 .
.
Скорость 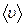 одинакова для всех молекул данного слоя и различна для разных слоёв. Вследствие теплового движения молекулы переходят из слоя в слой. За время Dt через площадку DS в обоих направлениях перейдёт одинаковое количество молекул:
одинакова для всех молекул данного слоя и различна для разных слоёв. Вследствие теплового движения молекулы переходят из слоя в слой. За время Dt через площадку DS в обоих направлениях перейдёт одинаковое количество молекул:
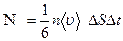 .
.
Попав в другой слой при соударении, молекула отдаёт или приобретает избыток импульса, в результате импульс быстро движущегося слоя убывает, а медленного - возрастает.
Молекулы, перешедшие из 1-го слоя во 2-й за Dt перенесут через DS импульс 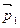 , из 2-го в 1-й -
, из 2-го в 1-й - 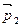 :
:
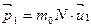 =
= 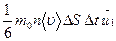 ,
, 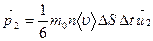 .
.
В результате через площадку DS за Dt перенесен импульс
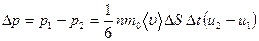 ,
,
где 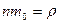 .
.
Каждая молекула, пересекая DS, переносит импульс, полученный в момент её последнего соударения с другой молекулой, происшедшего на расстоянии 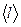 от DS, т.е. наименьшее расстояние, на котором возможно возникновение градиента скорости между слоями,
от DS, т.е. наименьшее расстояние, на котором возможно возникновение градиента скорости между слоями, 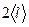 .
.
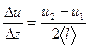
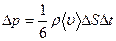
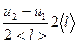 ;
; 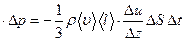 .
.
Знак ²минус² указывает, что импульс передается в направлении убывания скорости.
Поскольку
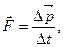
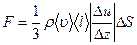 (7)
(7)
Из сравнения (6) и (7) следует, что
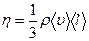 .
.
Большое значение имеет знание вязкости газов и жидкостей в военной технике - гидравлические амортизаторы, насосы, трубопроводы, движение летательных аппаратов в атмосфере.
в) Теплопроводность газов.
Явление теплопроводности возникает, если различные слои газа имеют разную температуру, т.е. обладают разной внутренней энергией. С макроскопической точки зрения явление теплопроводности состоит в переносе количества теплоты от более нагретого тела к менее нагретому.
Согласно эмпирическому закону Фурье
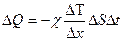 .
.
Количество теплоты 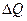 , переносимое за время Dt через площадь DS, пропорционально градиенту температуры
, переносимое за время Dt через площадь DS, пропорционально градиенту температуры 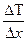 , площади DS и времени Dt.
, площади DS и времени Dt.
c - коэффициент теплопроводности
Знак ²минус ² указывает на то, что тепло переносится в сторону убывания температуры.
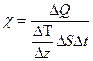
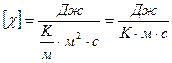 .
.
Коэффициент теплопроводности c - физическая величина, численно равная количеству теплоты, переносимой за единицу времени через единицу площади при градиенте температуры, равном единице.
С точки зрения МКТ перенос количества теплоты 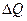 означает перенос через площадку DS некоторого количества кинетической энергии беспорядочного движения молекул.
означает перенос через площадку DS некоторого количества кинетической энергии беспорядочного движения молекул.
По аналогии с предыдущими случаями:
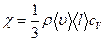 , где
, где 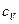 - удельная теплоемкость газа при постоянном объеме.
- удельная теплоемкость газа при постоянном объеме.
| Макроскопическая теория | Молекулярно-кинетическая теория | |||
| Явление | Перенесенная физическая величина | Закон переноса | Закон переноса | Коэффициент переноса |
| Диффузия | Масса | 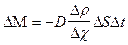
| 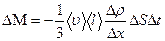
| 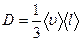
|
| Внутр. трение | Импульс | 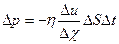
| 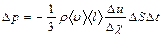
| 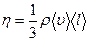
|
| Тепло-проводность | Внутренняя энергия | 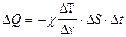
| 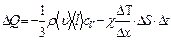
| 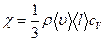
|
Дата добавления: 2016-11-04; просмотров: 1406;











