Колебания ротора с одним диском

Рассмотрим понятие критической частоты вращения на примере простого однодискового ротора, рис. 2

Он состоит из упругого невесомого вала на абсолютно жестких и идеально уравновешенного диска. Так как ротор является полностью симметричным, будем рассматривать его прогиб только в плоскости xy. В этом случае положение диска описывается двумя независимыми координатами (координатой x и координатой q ) и мы имеем систему с двумя степенями свободы.

Упругие свойства вала описываются симметричной матрицей коэффициентов податливости. Диск обладает массой, и соответствующими моментами инерции.

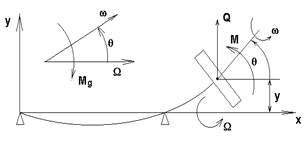
Рис. 1. Расчетная схема однодискового ротора

Колебания и устойчивость роторов определяется двумя видами вращения. Первый вид - вращение плоскости xy, в которой лежит изогнутая ось вала, вокруг оси проходящей через точки опор вала с угловой скоростью W. Этот вид кругового движения называется прецессией упругой оси ротора. Второй - это собственное вращение ротора ( вала и диска) вокруг изогнутой оси с абсолютной скоростью w. Скорости W и w независимы, соотношение этих двух скоростей может быть произвольным.

Следует иметь ввиду, что прецессия совершается как правило с частотой, равной частоте возмущающей силы L, т.е. W = L .

В результате кругового движения центра масс диска в точке крепления диска к валу возникает неуравновешенная сила

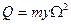(1)

где m – масса диска; y - линейное перемещение диска.

В результате сложного вращательного движения со стороны диска на вал действует изгибающий момент

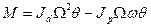, (2)

где J_d –диаметральный момент инерции диска; J_p- полярный момент инерции диска.

Первое слагаемое представляет собой инерционный момент диска от кругового движения плоскости упругой оси вала, второй член - гироскопический момент. Формула может быть записана в виде

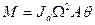(3)

где

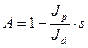(4)

где 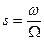- безразмерная величина.

Коэффициент А называется коэффициентом прецесии, его величина зависит от вида прецессии, задаваемым коэффициентом s т. е. от соотношения скоростей W и w.

Для оценки устойчивости ротора необходимо определить возможность существования прецессионного движения ротора при отсутствии внешних возмущающих сил. При таком движении внутренние силы и моменты упругости вала полностью уравновешиваются возникающими инерционными силами и моментами.

Условия при которых возможны такие прецессии, являются условиями потери устойчивости ротора, так как несущая способность вала становится равной нулю.

Предположим ротор может совершать свободное прецесионное движение. Прогиб вала и угол поворота под действием инерционных сил и моментов определяется уравнениями

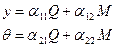(5)

где a₁₁, a₁₂, a₂₂ -коэффициенты влияния (податливости).

Заменяя силы и моменты их значениями по вышеприведенным формулам получаем систему из двух однородных уравнений

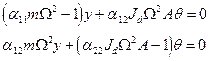(6)

Эти однородные уравнения имеют решения отличные от нуля при условии, что определитель, составленный из коэффициентов при неизвестных этих уравнений, равен нулю:

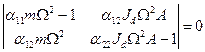(7)

Раскрывая определитель и подставляя А получим следующее частотное уравнение

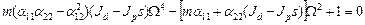(8)

Его корни (значения W и s) определяют виды прецессии и численные значения скоростей W и w. , при которых ротор теряет устойчивость.

В уравнении (8) величина 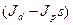зависит от вида прецессии. Для прямой синхронной прецессии 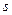=1. Для обратной синхронной прецессии 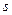= -1. Уравнение имеет бесчисленное множество решений, так как s может принимать любые значения. Эти решения можно представить в виде диаграммы соотношения скоростей W и w. (частотной диаграммы), рис.2.

На частотной диаграмме по оси ординат также может быть отложена величина L - частота возмущающей силы.

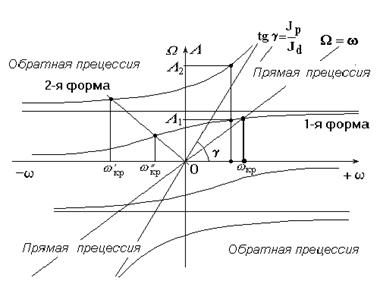
Рис. 2. Частотная диаграмма однодискового ротора

Чтобы рассчитать частоты собственных колебаний и построить 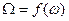можно принять следующие значения 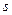: 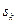= 2; 1; 0.3; 0.0; -0,5; -1; -2. Подставляя эти величины в уравнение (8) и решая его, для каждого вида прецессии получим частоты собственных колебаний .

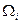Для того, чтобы найти значения критических скоростей 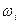, необходимо полученные значения 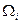умножить на 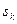. После чего можно построить диаграмму зависимостей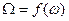

Горизонтальные асимптоты получаются из условий

W₁ = 0; W₂ = 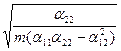(9)

Уравнение для нахождения наклонной асимптоты

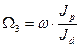(10)

т.е. наклонная асимптота проходит через начало координат под углом

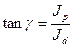. (12)

Коэффициенты влияния для рассматриваемой роторной системы могут быть определены по следующим формулам:

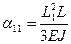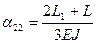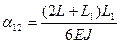; ; (13)

где

E - модуль упругости материала вала;

J – момент инерции поперечного сечения вала;

L₁ – длина консольного участка вала;

L - длина всего вала.

Анализ частотной диаграммы позволяет сделать следущие очень важные выводы.

1. Частота собственных колебаний ротора зависит от частоты вращения ротора. Этот феномен объясняется действием гироскопического момента, возникающего при вращении ротора с дисками.

2. На ротор могут действовать как внешние силы, так и внутренние, возникающие при вращении, вследствие остаточных дисбалансов. Для того, чтобы спроектировать ротор с низкой виброактивностью, необходимо знать соотношения между частотами возбуждающих сил и частотами собственных колебаний.

3. Если частота возбуждающей силы совпадает с частотой собственных колебаний ротора, то наступает явление резонанса, которое сопровождается большими вибрациями - большими прогибами вала ротора, нагрузками в опорах.

4. Частота вращения ротора, совпадающая с частотой собственных колебаний, называется критической частотой вращения, так как на этой скорости ротора возникает резонанс - частота возбуждения от неуравновешенной силы совпадает с частотой собственных колебаний. Неуравновешенные силы, как правило, вызывают прямую синхронную прецессию.

5. Для того, чтобы определить частоту вращения ротора, на которой возникает резонанс системы, необходимо из начала координат провести луч под углом 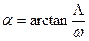до пересечения с кривыми частот собственных колебаний. Для определения критической частоты вращения, когда 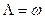, луч проводится под углом 45 градусов.

2.

ЛИТЕРАТУРА

1. Хронин Д.В. Колебания в двигателях летательных аппаратов. - М.: Машиностроение, 1980 г.