КОЭФФИЦИЕНТ СОПРОТИВЛЕНИЯ СИСТЕМЫ. СОПРОТИВЛЕНИЕ ТРУБОПРОВОДА
При определении потерь напора в трубопроводе при движении потока жидкости используется принцип наложения потерь. Потери напора по длине не зависят от местных потерь, а последние не зависят друг от друга, и все их можно складывать. Однако, используя принцип наложения потерь, следует учитывать влияние местных сопротивлений в случае, когда они должны находиться достаточно далеко друг от друга. Как уже рассматривалось раньше, в местных сопротивлениях в результате деформации потока возникает вихреобразование с образованием водоворотных областей. При близком расположении сопротивлений происходит наложение вихревых областей, что приводит к увеличению потерь напора. Выравнивание поля скоростей за местным сопротивлением, которое соответствует нормальному распределению в трубопроводе, происходит на некотором расстоянии, зависящем от интенсивности вихреобразования. Наибольшие расстояния между сопротивлениями должны быть при наличии арматуры (вентили, задвижки, краны), использующейся для регулирования расхода жидкости.
Установлено при проведении метрологических исследований, что эпюра скоростей за вентилем выравнивается в пределе на расстоянии до 50d (d - диаметр трубопровода), а за прямоугольным отводом - на расстоянии до 40d.
Согласно опытам автора по распределению скоростей в трубе на входе при наличии экрана 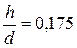 (h - расстояние от кромки трубы до экрана) эпюра скоростей выравнивалась на расстоянии
(h - расстояние от кромки трубы до экрана) эпюра скоростей выравнивалась на расстоянии 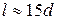 от плоскости входного отверстия. Водоворотная область (вихревая зона) распространялась на длину
от плоскости входного отверстия. Водоворотная область (вихревая зона) распространялась на длину 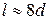 от входа.
от входа.
На практике расстояние между местными сопротивлениями следует рекомендовать при большой деформации потока 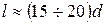 , при малой деформации -
, при малой деформации - 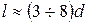 . Это объясняется тем, что искаженная эпюра скоростей практически не сказывается на потерях напора без учета геометрической высоты ее подъема.
. Это объясняется тем, что искаженная эпюра скоростей практически не сказывается на потерях напора без учета геометрической высоты ее подъема.
Потребный напор Н для обеспечения расхода жидкости в трубопроводе складывается из потерь напора по длине и местных потерь напора.
Рассмотрим трубопровод длиной 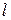 с постоянным диаметром d. По длине трубопровода встречается
с постоянным диаметром d. По длине трубопровода встречается 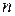 различных местных сопротивлений, значения коэффициентов которых соответственно
различных местных сопротивлений, значения коэффициентов которых соответственно  . Расход жидкости - Q. Коэффициент гидравлического трения -
. Расход жидкости - Q. Коэффициент гидравлического трения - 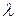 .
.
Зная величины 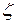 , определив среднюю скорость V и коэффициент гидравлического трения
, определив среднюю скорость V и коэффициент гидравлического трения 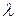 , можно вычислить суммарные потери напора как по длине, так и местные.
, можно вычислить суммарные потери напора как по длине, так и местные.
Потери напора по длине 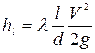 .
.
Местные потери 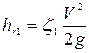 ,
,
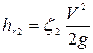 ,
,
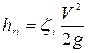 .
.
Сумма потерь напора в результате сложения частей системы уравнений (4.154) будет равна
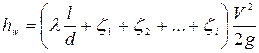 . (4.148)
. (4.148)
Сумма всех коэффициентов местных сопротивлений 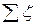 и коэффициента по длине
и коэффициента по длине 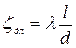 , характеризующего потери напора в трубопроводе, называется коэффициентом сопротивления системы
, характеризующего потери напора в трубопроводе, называется коэффициентом сопротивления системы 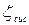 :
:
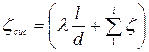 . (4.149)
. (4.149)
Таким образом, потребный напор
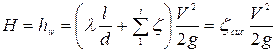 . (4.150)
. (4.150)
В случае если трубопровод состоит, например, из трех участков с различными диаметрами, на которых имеется несколько местных сопротивлений, потери напора выражаются через скоростной напор на одном из участков трубопровода. При определении скоростей для других участков используется уравнение неразрывности 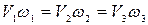 , где
, где 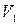 ,
, 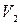 ,
, 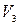 - средние скорости на участках;
- средние скорости на участках; 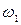 ,
,  ,
, 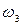 - площади поперечного сечения труб.
- площади поперечного сечения труб.
Первый трубопровод имеет длину и диаметр 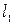 ,
, 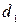 ; второй -
; второй - 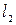 ,
, 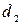 ; третий -
; третий - 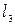 ,
, 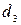 . На каждом участке, например, имеются по три сопротивления, и коэффициенты местных сопротивлений на первом участке
. На каждом участке, например, имеются по три сопротивления, и коэффициенты местных сопротивлений на первом участке 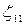 ,
, 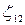 ,
, 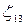 , на втором -
, на втором - 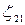 ,
, 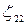 ,
, 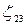 , на третьем -
, на третьем - 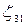 ,
, 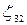 ,
, 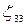 .
.
Потери напора на 1-м участке длиной 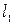
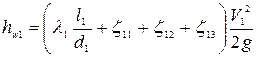 . (4.151)
. (4.151)
На 2-м участке длиной 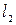
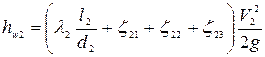 (4.152)
(4.152)
На 3-м участке длиной 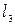
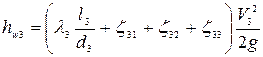 (4.153)
(4.153)
Выразим скорости 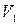 ,
, 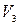 через
через 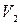 :
:
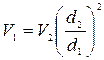 ,
, 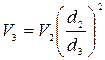 .
.
Подставив  и
и  в (4.151) и (4.153), получим потери напора и коэффициенты сопротивления системы для участков трубопровода:
в (4.151) и (4.153), получим потери напора и коэффициенты сопротивления системы для участков трубопровода:
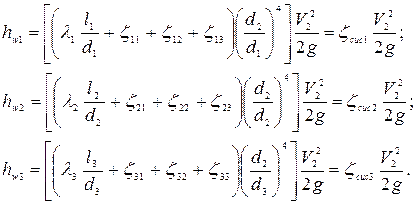 (4.155)
(4.155)
Коэффициент сопротивления системы для трубопровода будет равен сумме сопротивлений участков:
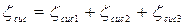 .
.
Следовательно, потери напора в трубопроводе и потребный напор
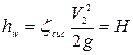 . (4.156)
. (4.156)
В некоторых случаях более удобно потери напора в трубопроводе представлять как функцию расхода.
Средняя скорость в трубе диаметром 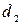
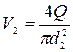 , скоростной напор
, скоростной напор
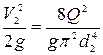 . (4.157)
. (4.157)
Подставим (4.157) в (4.156), тогда потери напора выразим через расход:
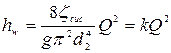 , (4.158)
, (4.158)
где 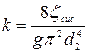 ,
, 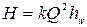 .
.
Величина 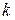 , являясь размерной, называется сопротивлением трубопровода. Пользуясь формулой (4.158), удобно выражать потери напора в зависимости от расхода, используя график. График зависимости потерь напора в трубопроводе от расхода называется характеристикой трубопровода:
, являясь размерной, называется сопротивлением трубопровода. Пользуясь формулой (4.158), удобно выражать потери напора в зависимости от расхода, используя график. График зависимости потерь напора в трубопроводе от расхода называется характеристикой трубопровода: 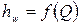 .
.

Рис. 4.26. Характеристики трубопроводов 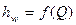
Формула (4.158) очень удобна для расчета трубопроводов. На рис. 4.26 показаны характеристики трубопроводов при 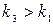 ,
, 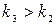 . Потери напора возрастают при одинаковом расходе с увеличением потерь как по длине, так и в местных сопротивлениях.
. Потери напора возрастают при одинаковом расходе с увеличением потерь как по длине, так и в местных сопротивлениях.
Дата добавления: 2016-10-26; просмотров: 1521;











