Методика расчета таблиц дожития с учетом влияния отдельных видов причин смертности на ожидаемую продолжительность жизни
Настоящая «Методика расчета таблиц дожития с учетом влияния отдельных видов причин смертности на ОПЖ» (далее – Методика) продолжает серию методических материалов, подготовленных Агентством Республики Казахстан по статистике, использование которых расширяет перечень показателей по демографической статистике, предоставляемые Агентством Республики Казахстан по статистике.
Ожидаемая продолжительность жизни населения, как один из показателей Целей развития тысячелетия, показывает очень важный аспект социального и экономического развития страны.
Одними из основных показателей цивилизованности страны, как считают ООН и ВОЗ, являются уровень здоровья и продолжительность жизни ее населения. На исследования в этой области практически во всех современных развитых государствах, а также во многих развивающихся тратятся государственные и частные средства, превосходящие траты в других областях.
В этой связи очень важно измерять влияние каждой причины смерти на ожидаемую продолжительность жизни, как одного из ключевых показателей измерения уровня демографического развития страны.
1. Основные понятия, используемые в Методологических рекомендациях
В данной Методике используются следующие определения и сокращения:
1) таблицы дожития (таблицы смертности) – это числовые модели смертности, служащие для характеристики ее общего уровня и возрастных особенностей в различных группах населения. Они представляют собой систему упорядоченных по возрасту и взаимосвязанных между собой рядов чисел, которые в своей совокупности описывают процесс вымирания некоторого теоретического поколения с фиксированной начальной численностью (корень таблицы). Обычно ее принимают равной некоторой степени 10, то есть 10 000, 100 000, 1 000 000 и тому подобное. Чаше всего за корень таблицы дожития принимают 100000;
2) таблицы смертности по причинам смерти - упорядоченные ряды взаимосвязанных величин, характеризующих влияние отдельных причин смерти на интенсивность возрастной смертности, дожитие до определенных возрастов, средней продолжительности предстоящей жизни и другой характеристики смертности;
3) смертность – процесс вымирания поколения и рассматривают ее как массовый статистический процесс, складывающийся из множества единичных смертей, наступающих в разных возрастах и определяющих в своей совокупности порядок вымирания реального или условного поколения;
4) общий коэффициент смертности – показатель, определяющий интенсивность смертности населения. Представляет собой отношение общего числа умерших в течение года к среднегодовой численности населения. Как правило, рассчитывается на 1 000 человек;
5) повозрастные коэффициенты смертности – отношение числа умерших в данном возрасте в течение календарного года к среднегодовой численности лиц данного возраста. Аналогично, коэффициенты смертности в данном возрасте по причинам смерти рассчитываются как отношения чисел умерших от указанных причин смерти к среднегодовой численности населения данного возраста;
6) коэффициент смертности по причинам смерти – отношение числа умерших от указанных причин смерти к среднегодовой численности населения по текущей оценке. В отличие от общих коэффициентов смертности они рассчитываются не на 1 000 человек, а на 100 тыс. человек. Общие коэффициенты смертности по основным классам причин смерти зависят от различий в возрастном составе умерших;
7) ожидаемая продолжительность жизни – это средний статистический показатель, характеризующий продолжительность жизни не отдельного индивидуума, а населения в целом. Этот показатель отражает число лет, которое в среднем предстояло бы прожить одному человеку из поколения родившихся при условии, что на протяжении всей жизни этого поколения уровень смертности в каждом возрасте останется таким, как в годы, для которых вычислен показатель. Ожидаемая продолжительность жизни для лиц, достигших возраста х – среднее число лет, которое предстояло бы прожить достигшим данного возраста при сохранении в каждом следующем возрасте современного уровня смертности.
8) проми́лле (от лат. pro mille, букв. «за тысячу») – одна тысячная доля, 1/10 процента. Обозначение – ‰. Обычно используется для обозначения доли чего-либо по отношению к целому. Количество нулей в обозначении (3 нуля) соответствует количеству нулей в числе 1000.
9) 2. Показатели таблиц смертности
2. Как и любая демографическая таблица, таблица смертности имеет шкалу. Шкала приведена в первой колонке таблицы и характеризует точное число полных лет, прошедших с момента рождения. Начальный возраст в таблице – 0 лет (момент рождения), конечный – w лет, возраст, к которому вымирает практически вся совокупность родившихся.
Первая колонка таблицы – точный возраст х. Это единственная независимая переменная, которая может измеряться в днях, месяцах (при изучении младенческой смертности), но, как правило, измеряется в годах. В зависимости от длины возрастного интервала n выделяют полные (n=1) и краткие (n=5 или n=10) таблицы смертности. В таблице 1 приведен пример краткой таблицы смертности.
Пример краткой таблицы смертности (Казахстан, мужчины, 2009 год)
| x | nmx | nqx | npx | lx | ndx | nLx | Tx | Ex | nαx |
| 0,0168 | 0,0167 | 0,9833 | 59,0 | 0,5 | |||||
| 0,0011 | 0,0044 | 0,9956 | 59,0 | 2,1 | |||||
| 0,0006 | 0,0030 | 0,9970 | 55,2 | 2,7 | |||||
| 0,0006 | 0,0030 | 0,9970 | 50,4 | 2,7 | |||||
| 0,0020 | 0,0100 | 0,9900 | 45,5 | 2,7 | |||||
| 0,0045 | 0,0223 | 0,9777 | 41,0 | 2,7 | |||||
| 0,0058 | 0,0286 | 0,9714 | 36,9 | 2,7 | |||||
| 0,0070 | 0,0344 | 0,9656 | 32,9 | 2,7 | |||||
| 0,0094 | 0,0460 | 0,9540 | 28,9 | 2,7 | |||||
| 0,0131 | 0,0636 | 0,9364 | 25,2 | 2,7 | |||||
| 0,0184 | 0,0882 | 0,9118 | 21,7 | 2,7 | |||||
| 0,0257 | 0,1212 | 0,8788 | 18,6 | 2,6 | |||||
| 0,0342 | 0,1582 | 0,8418 | 15,8 | 2,6 | |||||
| 0,0470 | 0,2112 | 0,7888 | 13,2 | 2,6 | |||||
| 0,0607 | 0,2645 | 0,7355 | 11,1 | 2,6 | |||||
| 0,0829 | 0,3439 | 0,6561 | 9,2 | 2,5 | |||||
| 0,1034 | 0,4102 | 0,5898 | 7,6 | 2,5 | |||||
| 0,1407 | 0,5153 | 0,4847 | 6,2 | 2,4 | |||||
| 85+ | 0,1908 | 1,0000 | 5,2 | 5,2 |
3. В таблицах смертности используются следующие показатели:
lx – число доживших до точного возраста х из начальной численности когорты. Начальная численность когорты (поколения) или корень таблицы принимается равной 100000 человек.
ndx – числа умирающих в интервале возраста от х до (х+n). Сумма всех значений ndx включает всех новорожденных:
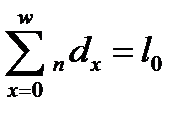 , ndx=lx – lx+n.
, ndx=lx – lx+n.
nqx – вероятность умереть в интервале возраста от x до х+n; nqx=ndx/lx для всех тех, кто дожил до возраста х.
npx – вероятность выжить к возрасту х+n для всех тех, кто дожил до возраста х;
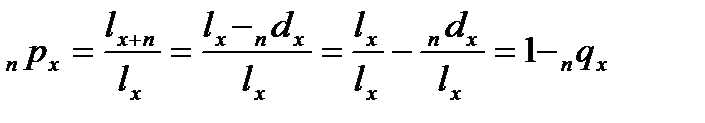 .
.
nLx – среднее число человеко-лет, прожитое в интервале возраста от х до х+n теми, кто дожил до начала данного интервала (lx). В общем виде выглядит следующим образом:
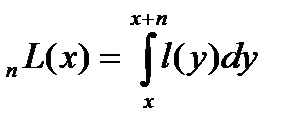
Приближенно, при использовании гипотезы равномерного распределения смертей в возрастном интервале, этот показатель рассчитывается как полусумма чисел доживающих до начала и конца возрастного интервала, умноженная на длину возрастного интервала n:
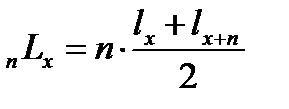
Однако, эта гипотеза будет слишком грубой для самых младших и самых старших возрастов.
nαx – среднее число человеко-лет, прожитых в интервале от x до x+n лет умершими в этом интервале или средняя продолжительность жизни в возрастном интервале от х до х+n. Этот показатель важен при построении таблиц смертности для условного поколения с использованием современных методов. В таблицах смертности для реальных поколений он вычисляется непосредственно и не имеет большого значения. В общем виде выглядит следующим образом:
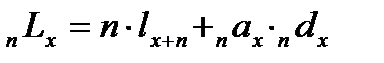
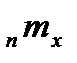 – табличный возрастной коэффициент смертности в возрастном интервале от х до х+n;
– табличный возрастной коэффициент смертности в возрастном интервале от х до х+n;
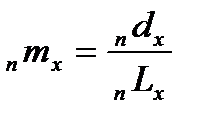
Тх – число человеко-лет жизни в возрасте х лет и старше: Tx=Lx+Lx+n+…+Lw
еx – ожидаемая продолжительность жизни в возрасте х лет: еx=Tx/lx
Чаще всего пользуются важнейшей демографической характеристикой смертности населения – ожидаемой продолжительностью жизни при рождении. При условии, что число умирающих на первом году жизни достаточно велико, может проявиться так называемый парадокс младенческой смертности, когда е1›е0. Она рассчитывается следующим образом: е0=T0/l0
Приведенные формулы не позволяют рассчитать значения показателей в последнем, открытом интервале (как правило, «85 лет и старше»). Для этого интервала число человеко-лет жизни рассчитывают следующим образом:
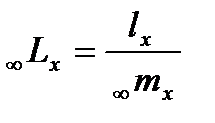
Где 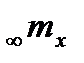 рассчитывают на основе данных реальной статистики, а lx берут из таблицы смертности. При этом в последнем возрастном интервале принимают
рассчитывают на основе данных реальной статистики, а lx берут из таблицы смертности. При этом в последнем возрастном интервале принимают 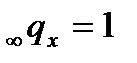 и
и 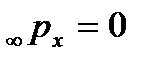 .
.
3. Основные методы построения таблицы дожития
Первые таблицы смертности были построены методом смертных списков (авторы: Дж. Граунт, Э. Галлей, К.Ф. Герман и другие). Этот метод используется при отсутствии данных о возрастной структуре населения и основан на следующих допущениях: медленное изменение чисел рождений, медленное изменение возрастной смертности, закрытое население. В качестве исходных статистических данных используется группировка умерших по возрастам. При этом отношение числа умерших в возрасте х к общему числу умерших в течение некоторого периода времени дает dx=Мх/М. Вычитая последовательно dx из l0=1, получаем ряд lx, а затем все остальные показатели таблицы.
Если при неизменном уровне рождаемости и смертности числа рождений меняются в геометрической прогрессии со знаменателем ek, то для расчета чисел умирающих dx получим следующую формулу:
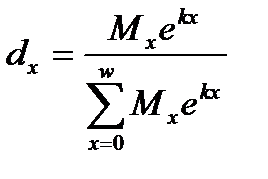
Этот метод был предложен Л. Эйлером и использован при расчете ряда таблиц смертности до появления демографического метода.
Для расчета современных таблиц смертности условного поколения используется так называемый демографический метод. Демографический метод построения таблиц смертности предполагает наличие не только данных о распределении умерших по возрастам, но и данных о возрастной структуре населения.
Исходным показателем при расчете таблиц этим методом служит возрастной коэффициент смертности, который приравнивается к табличному возрастному коэффициенту смертности. Ключевым моментом демографического метода построения таблиц смертности является переход от коэффициентов смертности к вероятностям умереть таблицы смертности. Для перехода к табличным вероятностям умереть используется следующую формулу:
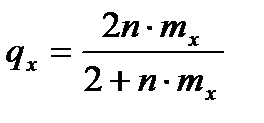
Данную формулу можно использовать для оценки показателей таблицы смертности во всех возрастах, кроме самых молодых и самых старых, где гипотеза равномерного распределения смертей не подтверждается. Для оценки вероятностей умереть в этих возрастах применяются специальные формулы, в которые вводится показатель nαx. Например, для детских возрастов (младше 5 лет) можно использовать следующие оценки nαx в зависимости от уровня смертности в соответствующих возрастах в следующей таблице:
| мужчины | женщины | |
| Оценки 1α0 | ||
| Если 1m0≥0,107 | 0,330 | 0,350 |
| Если 1m0<0,107 | 0,045+2,684*1m0 | 0,053+2,8*1m0 |
| Оценки 4α1 | ||
| Если 1m0≥0,107 | 1,352 | 1,361 |
| Если 1m0<0,107 | 1,651-2,816*1m0 | 1,522-1,518*1m0 |
Эта формула используется при допущении, что смерти распределены равномерно в интервале возраста от x до x+n. К ней можно перейти от показателей nLx и 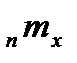 . Зависимость nqx от
. Зависимость nqx от 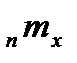 выглядит следующим образом:
выглядит следующим образом:
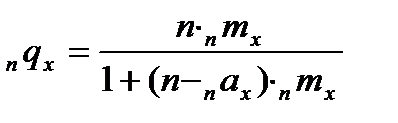 ,
,
Где n – длина возрастного интервала, nαx – среднее число человеко-лет, прожитых в интервале от x до x+n лет умершими в этом интервале.
Принимая во внимание тот факт, что функция дожития нелинейна на всем своем протяжении, американский демограф Т. Гревилл предложил в 1943 г. скорректированную формулу для перехода от реальных коэффициентов смертности к вероятностям умереть таблицы смертности:
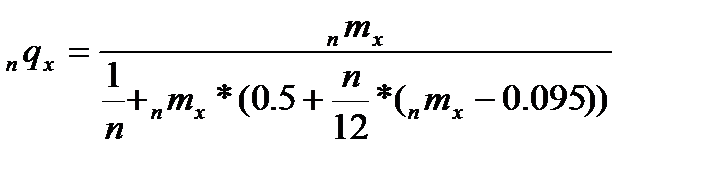 ,
,
Где х – точный возраст, n – длина возрастного интервала (шаг таблицы), nmx – возрастной коэффициент смертности, приведенный к 1, nqx – вероятность умереть в интервале возраста от х до x+n лет.
При расчете кратких таблиц смертности используется также метод В.В. Паевского, впервые реализованный для расчета таблиц смертности населения СССР 1926 – 1927 гг. Числа доживающих до возраста x+n рассчитываются по следующей формуле:
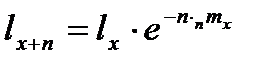 ,
,
Где lx – число доживающих до возраста х, а nmx – коэффициент смертности в интервале возраста от х до х+n.
4. Таблицы смертности по причинам смерти
Таблицы смертности по причинам смерти представляют собой дальнейшее развитие таблиц смертности. Обычно строят краткие таблицы смертности по причинам, в связи с тем, что число смертных случаев от ряда причин в отдельных возрастных группах может быть незначительным. Расчет показателей таблиц смертности по причинам основан на предположении, что интенсивность смертности от некоторой причины в данном возрасте не зависит от смертности от других причин в более молодых возрастах.
В таблицах смертности по причинам присутствуют следующие группы показателей:
1) Показатели, измеряющие фактический уровень смертности от отдельных причин:
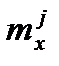 – коэффициент смертности в возрасте x от отдельной причины смерти j;
– коэффициент смертности в возрасте x от отдельной причины смерти j;
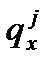 – вероятность умереть в возрасте x от отдельной причины смерти j;
– вероятность умереть в возрасте x от отдельной причины смерти j;
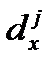 – числа умирающих в возрасте x от отдельной причины смерти j;
– числа умирающих в возрасте x от отдельной причины смерти j;
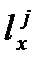 – доживающих до возраста x лет в совокупности лиц, которые когда-либо умрут от отдельной причины смерти j;
– доживающих до возраста x лет в совокупности лиц, которые когда-либо умрут от отдельной причины смерти j;
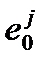 – средний возраст смерти от данной причины j или ожидаемая продолжительность жизни совокупности лиц
– средний возраст смерти от данной причины j или ожидаемая продолжительность жизни совокупности лиц 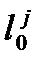 ;
;
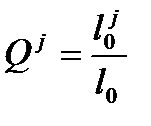 – вероятность для новорожденного умереть от j причины.
– вероятность для новорожденного умереть от j причины.
2) Чистые показатели таблиц смертности:
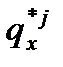 – вероятность смерти от отдельной причины;
– вероятность смерти от отдельной причины;
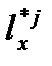 – числа доживающих.
– числа доживающих.
Если сумма фактических вероятностей умереть от всех причин равна общей вероятности смерти, то чистые вероятности смерти, благодаря предположению о независимости вероятностей умереть от разных причин, подчиняются следующему соотношению:
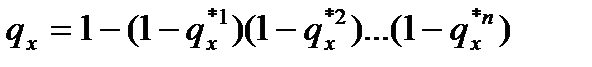 ,
,
где n – число причин смерти. При n=2 чистая вероятность смерти от двух причин в возрасте х равна 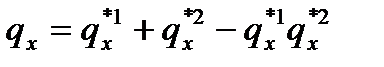 , где третье слагаемое выражает невозможность умереть одновременно от двух причин. Все остальные показатели вычисляются на основе чистых вероятностей умереть.
, где третье слагаемое выражает невозможность умереть одновременно от двух причин. Все остальные показатели вычисляются на основе чистых вероятностей умереть.
3) Гипотетические показатели:
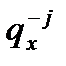 – вероятность умереть, характеризующая интенсивность уменьшения смертности в возрасте x при устранении причины смерти j;
– вероятность умереть, характеризующая интенсивность уменьшения смертности в возрасте x при устранении причины смерти j;
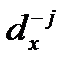 – числа умирающих в возрасте x при устранении смертности от причины j;
– числа умирающих в возрасте x при устранении смертности от причины j;
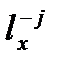 – доживающих до возраста x лет при устранении смертности от причиныj;
– доживающих до возраста x лет при устранении смертности от причиныj;
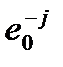 – прирост ожидаемой продолжительности жизни по сравнению с общей продолжительностью жизни при устранении смертности от причины j.
– прирост ожидаемой продолжительности жизни по сравнению с общей продолжительностью жизни при устранении смертности от причины j.
При наличии двух причин смерти 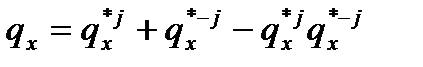 , откуда
, откуда 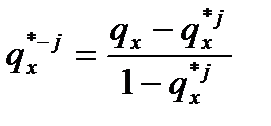 – вероятность смерти при устранении причины j равна чистой вероятности смерти от всех причин, кроме j.
– вероятность смерти при устранении причины j равна чистой вероятности смерти от всех причин, кроме j.
5. Таблица смертности от одной из причин
Для каждого возраста х и болезни j можно рассчитать доли wxj, которые занимают в общей смертности возраста х смертность от причины j. Для этого достаточно иметь распределение умерших по возрасту и по причинам смерти. При этом 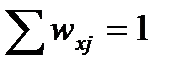 . По этим же долям можно распределить числа умирающих таблицы смертности:
. По этим же долям можно распределить числа умирающих таблицы смертности:
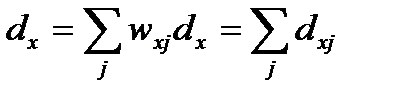 .
.
Для причины j получим ряд чисел умирающих от этой причины d0j,d1j,…, сумма членов которого не равна 1. Построенная таким образом таблица смертности не приведет к полному исчезновению исходной численности поколения. Вместо ожидаемой продолжительности жизни в данной таблице мы можем рассматривать средний возраст смерти от изучаемой причины, как если бы существовала только эта единственная причина смерти.
6. Таблица смертности от всех причин при условии исключения одной причины
В составе dx есть часть wjxdx умирающих от исключенной причины, и часть (1-wjx)dx умирающих от всех прочих причин. Рассматривая умерших от исключаемой причины как выбывших из-под наблюдения, введем поправку, аналогичную поправке на миграцию. При этом вводится предположение о независимости причин смерти. Получим условную вероятность смерти в возрасте х при исключении причины j:
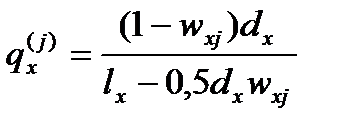
или после деления числителя и знаменателя на lx получим:
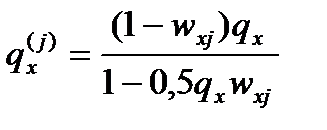
При этом предполагается, что все умершие от данной причины умирают в середине соответствующего возрастного интервала.
Пример: численность возрастной группы «60 лет» равна 50000. В этой группе между точными возрастами 60 и 61 год зарегистрировано 400 смертей от рака и 650 смертей от всех прочих причин.
Вероятность умереть при отсутствии смертности от рака была бы равна: 650/(50000-400/2)=13,05‰.
Вероятность умереть от всех причин: 1050/50000=21,0‰.
На основе полученного ряда 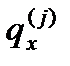 условных вероятностей смерти при исключении причины j можно рассчитать все остальные показатели таблицы смертности, включая ожидаемую продолжительность предстоящей жизни, которая будет больше е0 в обычной таблице смертности для всех причин.
условных вероятностей смерти при исключении причины j можно рассчитать все остальные показатели таблицы смертности, включая ожидаемую продолжительность предстоящей жизни, которая будет больше е0 в обычной таблице смертности для всех причин.
При исключении двух причин необходимо воспользоваться формулой:
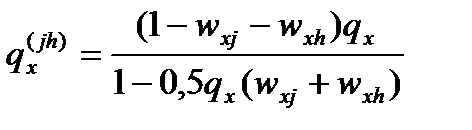 .
.
При этом нельзя ограничиться простым суммированием «выигрыша» от исключения двух причин, поскольку избежавший смерти от одной причины может умереть от другой.
Таблица дожития является одним из важных расчетов в измерении уровня смертности населения. Основные показатели таблицы дожития, в том числе ожидаемая продолжительность жизни при рождении является одним из показателей Целей развития тысячелетия.
Определение вклада каждой причины смерти в ожидаемую продолжительность жизни при рождении населения является ключевым аспектом в развитии не только демографической статистики, но и для развития здравохранения и охраны здоровья населения.
Литература
1. Бочаров П.П., Касимов Ю. Ф. Финансовая математика.: Учебник. – М.: Гардарики, 2002
2. Капитоненко В.В. Финансовая математика и ее приложения: Учебно-практическое пособие для ВУЗов. – М.: ПРИОР,1998
3. Касимова О.Ю. Введение в финансовую математику (анализ кредитных и инвестиционных операций). – М.: Анкил, 2001
4. Ковалев В.В. Методы оценки инвестиционных проектов.- М.: Финансы и статистика, 2003.
5. Ковалев В.В., Уланов В.А. Курс финансовых вычислений. – 2-е изд. – М.: Финансы и статистика, 2002.
6. Криничанский К.В. Математика финансового менеджмента: учебное пособие. – М.: Издательство «Дело и Сервис», 2006.
7. Кузнецов Б. Т. Финансовая математика: Учебное пособие для вузов – М.: Издательство «Экзамен», 2005.
8.Лукасевич И.Я. Анализ финансовых операций. Методы, модели, техника вычислений: Учебное пособие для вузов. – М.: Финансы, ЮНИТИ, 1998.
9. Малыхин В.И. Финансовая математика/ Учебное пособие для вузов.-.: ЮНИТИ-ДАНА, 1999
10. Мелкумов Я.С. Финансовые вычисления. Теория и практика: Учебно-справочное пособие. – М.:ИНФРА, 2002
11. Салин В.Н., Ситникова О.Ю. Техника финансово-экономических расчетов: Учебное пособие-М.: Финансы и статистика, 1998
12.Симчера В.М. Введение в финансовые и актуарные вычисления-М.: Финансы и статистика, 2003
13. Уланов В.А. Сборник задач по курсу финансовых вычислений/Под ред. Проф. В.В. Ковалева-М.: Финансы и статистика, 2000
14.Четыркин Е.М. Методы финансовых и коммерческих расчетов.-М.: «Дело-Ltd», 1995. гл. 12 «Изменение эффективности инвестиций»
Дата добавления: 2019-09-30; просмотров: 1221;











