Теоретико-множественный смысл произведения

<57 58 596061 62 63 >

Определение умножения натуральных чисел в аксиоматической теории основывается на понятии отношения «непосредственно следовать за» и сложении. В школьном курсе математики используется другое определение умножения, оно связано со сложением одинаковых слагаемых. Покажем, что оно вытекает из первого.

Теорема 4. Если b > 1, то произведение чисел а и b равно сумме b слагаемых, каждое из которых равно а.

Доказательство. Обозначим сумму b слагаемых, каждое из которых равно а, через а o b. И, кроме того, положим, что а o 1 = а. Тогда выражение а o (b + 1) будет означать, что рассматривается сумма b + 1 слагаемого, каждое из которых равно а, т.е. а o (b+ 1) = 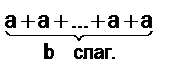. Сумму а + а + …+ а + а можно представить в виде выражения ( 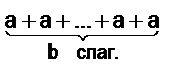) +а, которое равно а o b + а. Значит, операция аob обладает теми же свойствами, что и умножение, определенное в аксиоматической теории, а именно, а o 1 = а и а o (b + 1) = а o b + а. В силу единственности умножения получаем, что a o b = а × b.

Итак, если а и b - натуральные числа и b > 1, то произведение а × b можно рассматривать как сумму b слагаемых, каждое из которых равно а.

Умножение на 1 определяется так: а × 1 = а.

Если умножение рассматривается на множестве целых неотрицательных чисел, то к этим двум случаем надо добавить третий - определение умножения на нуль: а× 0 = 0.

Таким образом, получаем следующее определение умножения целых неотрицательных чисел.

Определение.Если а, b - целые неотрицательные числа, то произведением а × b называется число, удовлетворяющее следующим условиям:

1) а × b = 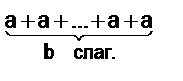, еслн b > 1;

2) а × b = а, если b = 1;

3) а × b = 0, если b = 0.

Случаю 1) этого определения можно дать теоретико-множественную трактовку. Если множества А₁, А₂, ..., А_b, имеют по а элементов каждое, причем никакие два из них не пересекаются, то их объединение А₁ È А₂È ...È А_b , содержит а × b элементов.

Таким образом, с теоретико-множественных позиций а × b (b > 1) представляет собой число элементов в объединении b множеств, каждое из которых содержит по а элементов и никакие два из них не пересекаются.

а × b = п (А₁ È А₂È ...È А_b) , если п (А₁) = п (А₂) = ... = п (А_b ) = а и А₁, А₂, ..., А_b попарно не пересекаются.

Взаимосвязь умножения натуральных чисел с объединением равночисленных попарно непересекающихся подмножеств позволяет обосновывать выбор действия умножения при решении текстовых задач.

Рассмотрим, например, такую задачу: «На одно пальто пришивают 4 пуговицы. Сколько пуговиц надо пришить на 3 таких пальто?» Выясним, почему она решается при помощи умножения.

В задаче речь идет о трех множествах, в каждом из которых 4 элемента. Требуется узнать число элементов в объединении этих трех множеств. Если n(А₁) = n(А₂) = n(А₃) = 4, то n(А₁È А₂È А₃) = n(А₁) + n (А₂) + n(А₃) = 4 + 4 + 4 = 4 ×3. Произведение 4×3 является математической моделью данной задачи. Так как 4 ×3 = 12, то получаем ответ на вопрос: на 3 пальто надо пришить 12 пуговиц.

Можно дать другое теоретико-множественное истолкование произведения целых неотрицательных чисел. Оно связано с понятием декартова произведения множеств.

Теорема 5. Пусть А и В - конечные множества. Тогда их декартово произведение также является конечным множеством, причем выполняется равенство: п(А´В) = п(А) × п(В).

Доказательство. Пусть даны множества А = (а₁, а₂, ..., а_п), В = (b₁, b₂, …, b_k), 741 ,причем k > 1. Тогда множество А´ В состоит из пар вида (а_i_,b_j), где 1£ i £n, 1 £ j £ k. Разобьем множество А ´ В на такие подмножества А₁, А₂, ..., А_k, что подмножество А_j, состоит из пар вида (а_1,b_j), (а_2,b_j),…, (а_n_,b_j).Число таких подмножеств равно k, т.е. числу элементов в множестве В. Каждое множество А_j состоит из n пар, и никакие два из этих множеств не содержат одну и ту же пару. Отсюда следует, что число элементов в декартовом произведении А´ В равно сумме k слагаемых, каждое из которых равно n, т.е. произведению чисел n и k. Таким образом, равенство n(А´ В) = n(А) × n(В) доказано при k > 1. При k = 1 оно тоже верно, так как в этом случае В содержит один элемент, например, В = {b}, а тогда А ´ В состоит из пар вида (а_1,b), (а_2,,b),…, (а_n_,b),число которых равно п. Поскольку n(А) = n, n(В) = 1, то и в этом случае имеем: n(А´ В) = n(А)×n(В)= n×1=n.

При k = 0 данное равенство также верно, поскольку В =Æ и n(А´Æ)=n(А)n(Æ)=а×0=0.

Из рассмотренной теоремы следует, что с теоретико-множественной точки зрения произведение а × b целых неотрицательных чисел есть число элементов в декартовом произведении множеств А и В, таких, что п(А) = а, п(В) = b.

а × b = п(А) × п(В) = п(А ´ В ).

Этот подход к определению умножения позволяет раскрыть теоретико-множественный смысл свойств умножения. Например, смысл равенства а×b = b×а состоит в том, что хотя множества А ´ В и В ´ А различны, они являются равномощными: каждой паре (а, b) из множества А ´ В можно поставить в соответствие единственную пару (b, а) из множества В ´ А, и каждая пара из множества В ´ А сопоставляется только одной паре из множества А ´ В. Значит, n(А ´ В) = n(В ´ А) и поэтому а × b = b × а.

Аналогично можно раскрыть теоретико-множественный смысл ассоциативного свойства умножения. Множества А ´ (В ´ С) и (А ´ В) ´ С различны, но они являются равномощными: каждой паре (а, (b, с)) из множества А ´ (В ´ С) можно поставить в соответствие единственную пару ((а, b), с) из множества (А ´ В) ´ С, и каждая пара из множества А ´ (В ´ С) сопоставляется единственной паре из множества (А ´ В) ´ С. Поэтому n(А´(В´С)) = n((А´ В)´С) и, следовательно, а(bс) = (а b)с.

Дистрибутивность умножения относительно сложения выводится из равенства А ´ (В È С) = (А ´ В) È (А ´ С), а дистрибутивность умножения относительно вычитания - из равенства А´(В \ С)= (А´В) \ (А´С).

В начальных курсах математики произведение целых неотрицательных чисел чаще всего определяют через сумму. Случаи а ´ 1 = а и а ´ 0 = 0 принимаются по определению.

<57 58 596061 62 63 >

Дата добавления: 2021-01-26; просмотров: 644;