Элементы ограничения многогранников
I. ГЕОМЕТРИЧЕСКАЯ КРИСТАЛЛОГРАФИЯ
Кристаллография –наука о кристаллах, их внешней форме, внутреннем строении, физических свойствах, процессах их образования и искусственного получения. У любого материального объекта существуют различные симметрийные уровни структурной организации. Минерал как природный объект – не исключение, а, наоборот, является одним из главных материальных объектов земной коры, обладающих всеми свойствами кристаллического вещества, на примере которого были изучены и выведены все основные законы симметрии кристаллов-многогранников.
Кристаллами называются твёрдые тела с упорядоченным внутренним строением пространственной решётки и имеющие вследствие этого форму многогранников.
Элементы ограничения многогранников
Многогранником называется объемное геологическое тело, отделенное от окружающего пространства элементами ограничения.
Элементами ограничения называют геометрические образы, отделяющие многогранник от окружающего пространства.
К элементам ограничения многогранника относятся грани, ребра, вершины, двугранные и многогранные углы.
Грани – это плоские поверхности, ограничивающие многогранник от внешней среды.
Рёбра – это прямые линии, по которым пересекаются грани.
Вершины – это точки, в которых пресекаются ребра.
Двугранные углы – это углы между двумя соседними гранями. Иначе, это углы при ребрах.
Многогранные углы – это углы между несколькими гранями, сходящимися в одной вершине. Иначе, это углы при вершинах.
Среди многогранных углов различают правильные и неправильные. Если при соединении концов ребер, исходящих из вершины многогранного угла, получается правильная геометрическая фигура (правильный треугольник, прямоугольник, ромб, квадрат, правильный шестиугольник и их производные), то образуется правильный многогранный угол. Если при этой же операции получается неправильная геометрическая фигура (неправильный многоугольник), то такой многогранный угол называется неправильным.
Различают следующие правильные многогранные углы.
1. Тригональный – при соединении концов ребер, исходящих из его вершины, образуется правильный треугольник (тригон): 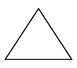
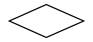 2. Ромбический 1-го рода – соединение концов ребер, исходящих из его вершины, дает фигуру в форме ромба:
2. Ромбический 1-го рода – соединение концов ребер, исходящих из его вершины, дает фигуру в форме ромба:

3. Ромбический 2-го рода – фигура, получаемая при соединении концов ребер, исходящих из его вершины, – прямоугольник:
 4. Тетрагональный – при соединении концов ребер, исходящих из его вершины, образуется квадрат (тетрагон):
4. Тетрагональный – при соединении концов ребер, исходящих из его вершины, образуется квадрат (тетрагон):
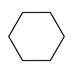
5. Гексагональный – соединение концов ребер, исходящих из его вершины, дает правильный шестиугольник (гексагон):
Данные пять правильных многогранных углов называются основными.
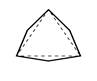 Кроме того, из тригонального, тетрагонального и гексагонального углов путем их удвоения образуются следующие три производных правильных многогранных угла.
Кроме того, из тригонального, тетрагонального и гексагонального углов путем их удвоения образуются следующие три производных правильных многогранных угла.
1. Дитригональный – образуется путем удвоения граней, составляющих тригональный угол (дитригон):
2. Дитетрагоналный – образуется при удвоении числа граней тетрагонального угла (дитетрагон):

3. Дигксагональный – образуется путем удвоения числа граней, ограничивающих гексагональный угол (дигексагон):
Во всех производных правильных многогранных углах двугранные углы равны через один, а все стороны фигуры, образованной при соединении концов ребер, исходящих из вершины, равны.
Таким образом, существует всего 8 правильных многогранных углов. Все остальные многогранные углы являются неправильными. Их возможно бесконечное количество.
Между элементами ограничения многогранников существует математическая зависимость, характеризуемая формулой Эйлера-Декарта: Г (грани) + В (вершины) = Р (ребра) + 2. Например, в кубе 6 граней, 8 вершин и 12 рёбер.
Отсюда: 6+8=12+2. 
Дата добавления: 2016-10-26; просмотров: 3021;











