Отправитель и получатель. Сообщения и шифрование 2 глава
У полиалфавитных подстановочных шифров множественные однобуквенные ключи, каждый из которых используется для шифрования одного символа открытого текста. Первым ключом шифруется первый символ открытого текста, вторым ключом - второй символ, и так далее. После использования всех ключей они повторяются циклически. Если применяется 20 однобуквенных ключей, то каждая двадцатая буква шифруется тем же ключом. Этот параметр называется периодом шифра. В классической криптографии шифры с длинным периодом было труднее раскрыть, чем шифры с коротким периодом. Использование компьютеров позволяет легко раскрыть подстановочные шифры с очень длинным периодом.
Шифр с бегущим ключом (иногда называемый книжным шифром), использующий один текст для шифрования другого текста, представляет собой другой пример подобного шифра. И хотя период этого шифра равен длине текста, он также может быть легко взломан [576,794].
Перестановочные шифры
В перестановочном шифре меняется не открытый текст, а порядок символов. В простом столбцовом перестановочном шифре открытый текст пишется горизонтально на разграфленном листе бумаги фиксированной ширины, а шифротекст считывается по вертикали (см. Рис.-4). Дешифрирование представляет собой запись шифротекста вертикально на листе разграфленной бумаги фиксированной ширины и затем считывание открытого текста горизонтально.
Криптоанализ этих шифров обсуждается в [587,1475]. Так как символы шифротекста те же, что и в открытом тексте, частотный анализ шифротекста покажет, что каждая буква встречается приблизительно с той же частотой, что и обычно. Это даст криптоаналитику возможность применить различные методы, определяя правильный порядок символов для получения открытого текста. Применение к шифротексту второго перестановочного фильтра значительно повысит безопасность. Существуют и еще более сложные перестановочные фильтры, но компьютеры могут раскрыть почти все из них.
Немецкий шифр ADFCVX, использованный в ходе Первой мировой войны, представлял собой перестановочный фильтр в сочетании с простой подстановкой. Этот для своего времени очень сложный алгоритм был раскрыт Жоржем Пенвэном (Georges Painvin), французским криптоаналитиком [794].
Хотя многие современные алгоритмы используют перестановку, с этим связана проблема использования большого объема памяти, а также иногда требуется работа с сообщениями определенного размера. Подстановка более обычна.
Роторные машины
В 1920-х годах для автоматизации процесса шифрования были изобретены различные механические устройства. Большинство использовало понятие ротора, механического колеса, используемого для выполнения подстановки.
Роторная машина, включающая клавиатуру и набор роторов, реализует вариант шифра Вигенера. Каждый ротор представляет собой произвольное размещение алфавита, имеет 26 позиций и выполняет простую подстановку. Например, ротор может быть использован для замены "A" на "F", "B" на "U", "C'' на "I" и так далее. Выходные штыри одного ротора соединены с входными штырями следующего ротора.
Открытый текст:COMPUTER GRAPHICS MAY BE SLOW BUT AT LEAST IT'S EXPENSIVE.
COMPUTERGR
APHICSMAYB
ESLOWBUTAT
LEASTITSEX
PENSIVE
Шифротекст:CAELP OPSEE MHLAN PIOSS UCWTI TCBIV EMUTE RATSG YAERB TX
Рис.-4. Столбцовый перестановочный фильтр.
Например, в четырехроторной машине первый ротор может заменять "A" на "F", второй - "F" на "Y", третий - "Y" на "E" и четвертый - "E" на "C", "C" и будет конечным шифротекстом. Затем некоторые роторы смещаются, и в следующий раз подстановки будут другими.
Именно комбинация нескольких роторов и механизмов, движущих роторами, и обеспечивает безопасность машины. Так как роторы вращаются с различной скоростью, период для n-роторной машины равен 26n. Некоторые роторные машины также могут иметь различные положения для каждого ротора, что делает криптоанализ еще более бессмысленным.
Самым известным роторным устройство является Энигма (Enigma). Энигма использовалась немцами во Второй мировой войне. Сама идея пришла в голову Артуру Шербиусу (Arthur Scherbius) и Арвиду Герхарду Дамму (Arvid Gerhard Damm) в Европе. В Соединенных Штатах она была запатентована Артуром Шербиусом [1383]. Немцы значительно усовершенствовали базовый проект для использования во время войны.
У немецкой Энигмы было три ротора, котроые можно было выбрать из пяти возможных, коммутатор, который слегка тасовал открытый текст, и отражающий ротор, который заставлял каждый ротор обрабатывать открытый текст каждого письма дважды. Несмотря на сложность Энигмы, она была взломана в течение Второй мировой войны. Сначала группа польских криптографов взломала немецкую Энигму и объяснила раскрытый алгоритм англичанам. В ходе войны немцы модифицировали Энигму, а англичане продолжали криптоанализ новых версий. Объяснение работы роторных шифров и способов их раскрытия можно найти в [794, 86, 448, 498, 446, 880, 1315, 1587, 690]. В двух следующих отчетах увлекательно рассказывается о взломе Энигмы [735, 796].
Для дальнейшего чтения
Данная книга не является книгой по классической криптографии, поэтому далее я не буду подробно останавливаться на этих предметах. Прекрасными книгами по докомпьютерной криптологии являются [587, 1475]. [448] содержит современный криптоанализ шифровальных машин. Дороти Деннинг (Dorothy Denning) рассматривает многие из этих шифров в [456], а [880] содержит беспристрастный сложный математический анализ тех же самых шифров. Другим описанием старой криптографии, описывающим аналоговую криптографию, является [99]. Прекрасный обзор выполнен в статье [579]. Великолепны также книги по исторической криптографии Дэвида Кана [794, 795, 796].
1.4 Простое XOR
XOR представляет собой операцию "исключающее или": '^' в языке C или Q в математической нотации. Это обычная операция над битами:
0 Å 0 = 0
0 Å 1 = 1
1 Å 0 = 1
1 Å 1 = 0
Также заметим, что:
a Å a = 0
a Å b Å b = a
Казалось бы, запутанный алгоритм простого XOR по сути является ничем иным, как полиалфавитным шифром Вигенера. Здесь он упоминается только из-за распространенности в коммерческих программных продуктах, по крайней мере в мире MS-DOS и Macintosh [1502, 1387]. К сожалению, если о программе компьютерной безопасности заявляется, что это "патентованный" алгоритм шифрования, значительно более быстрый, чем DES, то скорее всего используется какой-то вариант следующего.
/* Использование: crypto key input_file output_file */
void main (int argc, char *argv[])
{
FILE *fl, *fo;
char *cp;
int c;
if ((cp = argv[l]) && *cp!= '\0') {
if ((fi = fopen(argvl[2], "rb")) != NULL) {
if ((fo = fopen(argv[3], "wb")) != NULL) {
while ((c = getc(fi)) != EOF) {
if (!*cp) cp = argv[1];
c^= *(cp++);
putc(c,fo);
}
fclose(fo);
}
fclose(fi);
}
}
}
Это симметричный алгоритм. Открытый текст подвергается операции "исключающее или" вместе с ключевым текстом для получения шифротекста. Так как повторное применение операции XOR восстанавливает оригинал для шифрования и дешифрирования используется одна и та же программа:
P Å K = C
C Å K = P
Настоящей безопасности здесь никогда не было. Этот тип шифрования легко вскрывается, даже без компьютера [587, 1475]. Его взлом на компьютере занимает несколько секунд.
Предположим, что открытый текст использует английский язык. Более того, пусть длина ключа любое небольшое число байт. Ниже описано, как взломать этот шифр:
1. Определим длину ключа с помощью процедуры, известной как подсчет совпадений [577]. Применим операцию XOR к шифротексту, используя в качестве ключа сам шифротекст с различными смещениями, и подсчитаем совпадающие байты. Если величина смещения кратна длине ключа, то совпадет свыше 6 процентов байтов. Если нет, то будут совпадать меньше чем 0.4 процента (считая, что обычный ASCII текст кодируется случайным ключом, для других типов открытых текстов числа будут другими). Это называется показателем совпадений. Минимальное смещение от одного значения, кратного длине ключа, к другому и есть длина ключа.
2. Сместим шифротекст на эту длину и проведем операцию XOR для смещенного и оригинального шифротекстов. Результатом операции будет удаления ключа и получение открытого текста, подвергнутого операции XOR с самим собой, смещенным на длину ключа. Так как в английском языке на один байт приходится 1.3 бита действительной информации (см раздел 11.1), существующая значительная избыточность позволяет определить способ шифрования.
Несмотря на это, количество поставщиков программного обеспечения, навязывающих этот игрушечный алгоритм в качестве "почти такого же безопасного как DES", впечатляет [1387]. Именно этот алгоритм (с 160‑битным повторяющимся "ключом") NSA в конце концов разрешило использовать в цифровых телефонных сотовых сетях для закрытия голоса. XOR может защитить ваши файлы от младшей сестры, но настоящего криптоаналитика задержит лишь на считанные секунды.
1.5 Одноразовые блокноты
Поверите или нет, но идеальный способ шифрования существует. Он называется одноразовым блокнотом и был изобретен в 1917 году Мэйджором Джозефом Моборном (Major Joseph Mauborgne) и Гилбертом Вернамом (Gilbert Vernam) из AT&T [794]. (Фактически одноразовый блокнот представляет собой особый случай пороговой схемы, см. раздел 3.7.) В классическом понимании одноразовый блокнот является большой неповторяющейся последовательностью символов ключа, распределенных случайным образом, написанных на кусочках бумаги и приклеенных к листу блокнота. Первоначально это была одноразовая лента для телетайпов. Отправитель использовал каждый символ ключа блокнота для шифрования только одного символа открытого текста. Шифрование представляет собой сложение по модулю 26 символа открытого текста и символа ключа из одноразового блокнота.
Каждый символ ключа используется только единожды и для единственного сообщения. Отправитель шифрует сообщения и уничтожает использованные страницы блокнота или использованную часть ленты. Получатель, в свою очередь, используя точно такой же блокнот, дешифрирует каждый символ шифротекста. Расшифровав сообщение, получатель уничтожает соответствующие страницы блокнота или часть ленты. Новое сообщение - новые символы ключа. Например, если сообщением является:
ONETIMEPAD
а ключевая последовательность в блокноте:
TBFRGFARFM
то шифротекст будет выглядеть как:
IPKLPSFHGQ
так как
Q + T mod 26 = I
N + B mod 26 = P
E + F mod 26 = K
и т.д.
В предположении, что злоумышленник не сможет получить доступ к одноразовому блокноту, использованному для шифрования сообщения, эта схема совершенно безопасна. Данное шифрованное сообщение на вид соответствует любому открытому сообщению того же размера.
Так как все ключевые последовательности совершенно одинаковы (помните, символы ключа генерируются случайным образом), у противника отсутствует информация, позволяющая подвергнуть шифротекст криптоанализу. Кусочек шифротекста может быть похож на:
POYYAEAAZX
что дешифрируется как:
SALMONEGGS
или на:
BXEGBMTMXM
что дешифрируется как:
GREENFLUID
Повторю еще раз: так как все открытые тексты равновероятны, у криптоаналитика нет возможности определить, какой из открытых текстов является правильным. Случайная ключевая последовательность, сложенная с неслучайным открытым текстом, дает совершенно случайный шифротекст, и никакие вычислительные мощности не смогут это изменить.
Необходимо напомнить, что символы ключа должны генерироваться случайным образом. Любые попытки вскрыть такую схему сталкиваются со способом, которым создается последовательность символов ключа. Использование генераторов псевдослучайных чисел не считается, у них всегда неслучайные свойства. Если вы используете действительно случайный источник - это намного труднее, чем кажется на первый взгляд, см. раздел 17.14 - это совершенно безопасно.
Другой важный момент: ключевую последовательность никогда нельзя использовать второй раз. Даже если вы используете блокнот размером в несколько гигабайт, то если криптоаналитик получит несколько текстов с перекрывающимися ключами, он сможет восстановить открытый текст. Он сдвинет каждую пару шифротекстов относительно друг друга и подсчитает число совпадений в каждой позиции. Если шифротексты смещены правильно, соотношение совпадений резко возрастет - точное значение зависит от языка открытого текста. С этой точки зрения криптоанализ не представляет труда. Это похоже на показатель совпадений, но сравниваются два различных "периода" [904]. Не используйте ключевую последовательность повторно.
Идея одноразового блокнота легко расширяется на двоичные данные. Вместо одноразового блокнота, состоящего из букв, используется одноразовый блокнот из битов. Вместо сложения открытого текста с ключом одноразового блокнота используйте XOR. Для дешифрирования примените XOR к шифротексту с тем же одноразовым блокнотом. Все остальное не меняется, и безопасность остается такой же совершенной.
Все это хорошо, но существует несколько проблем. Так как ключевые биты должны быть случайными и не могут использоваться снова, длина ключевой последовательности должна равняться длине сообщения. Одноразовый блокнот удобен для нескольких небольших сообщений, но его нельзя использовать для работы по каналу связи с пропускной способностью 1.544 Мбит/с. Вы можете хранить 650 Мбайт случайных данных на CD‑ROM, но и тут есть проблемы. Во первых, вам нужно только две копии случайных битов, но CD-ROM экономичны только при больших тиражах. И во вторых, вам нужно уничтожать использованные биты. Для CD‑ROM нет другой возможности удалить информацию, кроме как физически разрушить весь диск. Гораздо больше подходит цифровая лента.
Даже если проблемы распределения и хранения ключей решены, вам придется точно синхронизировать работу отправителя и получателя. Если получатель пропустит бит (или несколько бит пропадут при передаче), сообщение потеряет всякий смысл. С другой стороны, если несколько бит изменятся при передаче (и ни один бит не будет удален или добавлен - что гораздо больше похоже на влияние случайного шума), то лишь эти биты будут расшифрованы неправильно. Но одноразовый блокнот не обеспечивает проверку подлинности.
Одноразовые блокноты используются и сегодня, главным образом для сверхсекретных каналов связи с низкой пропускной способностью. По слухам "горячая линия" между Соединенными Штатами и бывшим Советским Союзом (а действует ли она сейчас?) шифруется с помощью одноразового блокнота. Многие сообщения советских шпионов зашифрованы с использованием одноразовых блокнотов. Эти сообщения нераскрыты сегодня и навсегда останутся нераскрытыми. На этот факт не повлияет время работы суперкомпьютеров над этой проблемой. Даже когда враги из созвездия Андромеды приземлят свои тяжелые корабли с компьютерами немыслимой мощности, и они не смогут прочесть сообщения советских шпионов, зашифрованные с помощью одноразовых (если, конечно, они не смогут вернуться в прошлое и добыть нужные одноразовые блокноты).
1.6 Компьютерные алгоритмы
Существует множество компьютерных алгоритмов. Следующие три используются чаще всего:
— DES (Data Encryption Standard, стандарт шифрования данных) - самый популярный компьютерный алгоритм шифрования, является американским и международным стандартом. Это симметричный алгоритм, один и тот же ключ используется для шифрования и дешифрирования.
— RSA (назван в честь создателей - Ривеста (Rivest), Шамира (Sharnir) и Эдлмана (Adleman)) - самый популярный алгоритм с открытым ключом. Используется и для шифрования, и для цифровой подписи.
— DSA (Digital Signature Algorithm, алгоритм цифровой подписи, используется как часть стандарта цифровой подписи, Digital Signature Standard) - другой алгоритм с открытым ключом. Используется только для цифровой подписи, не может быть использован для шифрования.
Именно эти и подобные алгоритмы описываются в этой книге.
1.7 Большие числа
На протяжении всей книги я использую различные большие числа для описания различных вещей в криптографии. Так как легко заблудиться в этих числах и их значениях, физические аналоги некоторых чисел приведены в Табл. -1.
Эти числа оцениваются по порядку величины и были отобраны из различных источников. Многие астрофизические значения объясняются в работе Фримана Дайсона (Freeman Dyson), "Время без конца: физика и биология в открытой Вселенной" ("Time Without End: Physics and Biology in an Open Universe") в Reviews of Modem Physics, v. 52, n. 3, July 1979, pp. 447-460. Смертность в результате автокатастроф рассчитана с помощью статистики Министерства транспорта (163 смерти миллион человек в 1993 году и для средней продолжительности жизни 69.7 года.
Табл. -1. Большие числа
| Физический аналог | Число |
| Вероятность быть убитым молнией (в течение дня) | 1 из 9 миллиардов (233) |
| Вероятность выиграть главный приз в государственной лотерее США | 1 из 4000000 (222) |
| Вероятность выиграть главный приз в государственной лотерее США и быть убитым молнией в течение того же дня | 1 из261 |
| Вероятность утонуть (в США в течение года) | 1 из 59000 (216) |
| Вероятность погибнуть в автокатастрофе (в США в году) | 1 из 6100 (213) |
| Вероятность погибнуть в автокатастрофе (в США в течение времени жизни) | 1 из 88 (27) |
| Время до следующего оледенения | 14000 (214) лет |
| Время до превращения Солнца в сверхновую звезду | 109 (230) лет |
| Возраст планеты | 109 (230) лет |
| Возраст Вселенной | 1010 (234) лет |
| Число атомов планеты | 1051 (2170) |
| Число атомов Солнца | 1057 (2190) |
| Число атомов галактики | 1067 (2223) |
| Число атомов Вселенной | 1077 (2265) |
| Объем Вселенной | 1084 (2280) см 3 |
| Если Вселенная конечна: | |
| Полное время жизни вселенной | 1011 (237) лет |
| 1018 (261) секунд | |
| Если Вселенная бесконечна: | |
| Время до остывания легких звезд | 1014 (247) лет |
| Время до отрыва планет от звезд | 1015 (250) лет |
| Время до отрыва звезд от галактик | 1019 (264) лет |
| Время до разрушения орбит гравитационной радиацией | 1020 (267) лет |
| Время до разрушения черных дыр процессами Хокинга | 1064 (2213) лет |
| Время до превращения материи в жидкость при нулевой температуре | 1065 (2216) лет |
| Время до превращения материи в твердое тело |  лет лет
|
| Время до превращения материи в черную дыру | 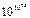 лет лет
|
Часть I
КРИПТОГРАФИЧЕСКИЕ
ПРОТОКОЛЫ
2 Элементы протоколов
2.1 Введение в протоколы
Смысл криптографии - в решении проблем. (По сути, в этом состоит и смысл использования компьютеров, о чем многие пытаются забыть.) Криптография решает проблемы секретности, проверки подлинности, целостности и человеческой нечестности. Вы можете выучить все о криптографических алгоритмах и методах, но они представляют только академический интерес, если не используются для решения какой-нибудь проблемы. Именно поэтому мы собираемся сначала взглянуть на протоколы.
Протокол - это порядок действий, предпринимаемых двумя или более сторонами, предназначенный для решения определенной задачи. Это важное определение. "Порядок действий" означает, протокол выполняется в определенной последовательности, с начала до конца. Каждое действие должно выполняться в свою очередь и только после окончания предыдущего. "Предпринимаемых двумя или более сторонами" означает, что для реализации протокола требуется по крайней мере два человека, один человек не сможет реализовать протокол. Человек в одиночку может выполнить некоторые действия, решая задачу (например, покупая торт), но это не протокол. (Для того, чтобы получился настоящий протокол, кто-то должен съесть торт.) Наконец, "предназначенный для решения определенной задачи" означает, что протокол должен приводить к какому-то результату. Что-то, похожее на протокол, но не решающее никакой задачи - это не протокол, это потеря времени. У протоколов есть также и другие характеристики:
— Каждый участник протокола должен знать протокол и последовательность составляющих его действий.
— Каждый участник протокола должен согласиться следовать протоколу.
— Протокол должен быть непротиворечивым, каждое действие должно быть определено так, чтобы не было возможности непонимания.
— Протокол должен быть полным, каждой возможной ситуации должно соответствовать определенное действие.
В этой книге каждый протокол организован как некоторый порядок действий. Выполнение протокола происходит по действиям, линейно, пока не будет команды перейти к следующему действию. Каждое действие включает по крайней мере одно из двух: вычисления, выполняемые одной или несколькими сторонами, или сообщения, которыми обмениваются стороны.
Криптографический протокол - это протокол, использующий криптографию. Стороны могут быть друзьями и слепо доверять друг другу или врагами и не верить друг другу даже при сообщении времени суток. Криптографический протокол включает некоторый криптографический алгоритм, но, вообще говоря, предназначение протокола выходит за рамки простой безопасности. Участники протокола могут захотеть поделиться секретом друг с другом, совместно генерировать случайную последовательность, подтвердить друг другу свою подлинность или подписать контракт в один и тот же момент времени. Смысл использования криптографии в протоколе - в предотвращении или обнаружении вредительства и мошенничества. Если вы никогда не сталкивались с подобными протоколами, они могут радикально изменить ваше представление о том, что недоверяющие друг другу стороны могут выполнить, используя компьютерную сеть. Общее правило можно сформулировать следующим образом:
— Невозможно сделать или узнать больше, чем определено в протоколе.
Это гораздо сложнее, чем кажется. В следующих нескольких главах я рассматриваю множество протоколов. В некоторых из них один из участников может обмануть другого. В других, злоумышленник может взломать протокол или узнать секретную информацию. Ряд протоколов проваливаются, так как их разработчики недостаточно тщательно определяли требования. Другие проваливаются из-за того, что их разработчики недостаточно тщательно анализировали свои протоколы. Как и для алгоритмов, гораздо легче доказать возможную небезопасность протокола, чем его полную безопасность.
Смысл протоколов
В повседневной жизни почти для всего существуют неформальные протоколы: заказ товаров по телефону, игра в покер, голосование на выборах. Никто не задумывается об этих протоколах, они вырабатывались в течение длительного времени, все знают, как ими пользоваться, и они работают достаточно хорошо.
Сегодня все больше и больше людей общаются не лично, а используя компьютерную сеть. Для тех же вещей, которые люди делают, не задумываясь, компьютерам нужны формальные протоколы. Когда вы переезжаете из государства в государство и обнаруживаете кабинку, совершенно отличающуюся от той, к которой вы привыкли, вы легко адаптируетесь. Компьютеры далеко не так гибки.
Честность и безопасность многих протоколов человеческого общения основаны на личном присутствии. Разве вы дадите незнакомцу кучу денег, чтобы он купил для вас что-нибудь в бакалее? Сядете ли вы играть в покер с тем, кто жульничает, сдавая карты? Пошлете ли вы свой избирательный бюллетень правительству, не будучи уверенным в тайности такого голосования?
Наивно считать, что пользователи компьютерных сетей всегда честны. Также наивно считать, что всегда честны разработчики компьютерных сетей. Для большинства из них это именно так, но даже несколько жуликов могут принести много вреда. Формализируя протоколы, можно проверить способы, используемые жуликами для взлома протоколов. Так мы можем разработать протоколы, устойчивые к взлому.
Кроме формализации действий, протоколы позволяют абстрагироваться при решении задачи от способа решения. Протокол связи один и тот же и на PC, и на VAX. Можно проверить протокол, не вдаваясь в детали его реализации. Когда мы убедимся в надежности протокола, его можно будет реализовать где угодно от компьютеров до телефонов и интеллектуальных тостеров.
Игроки
Для демонстрации работы протоколов я использую несколько игроков (см. Табл. -1). Первые двое - это Алиса и Боб. Они участвуют во всех двусторонних протоколах. Как правило, Алиса (Alice) начинает все протоколы, а Боб (Bob) отвечает. Если для протокола нужна третья или четвертая сторона, в игру вступают Кэрол (Carol) и Дэйв (Dave). Другие игроки играют специальные вспомогательные роли, они будут представлены позже.
Протоколы с посредником
Посредник - это незаинтересованная третья сторона, которой доверено завершение протокола (см. Рис. -1 (а)). Незаинтересованность означает, что у посредника нет заинтересованности в результате работы протокола и склонности к одной из сторон. "Доверено" означает, что все участники протокола принимают все, что скажет посредник за истину, все его действия - как правильные, и уверены в том, что посредник выполнит свою часть протокола. Посредники помогают реализовать работу протоколов взаимодействия недоверяющих друг другу сторон.
В реальном мире в качестве посредников часто выступают юристы. Например, Алиса продает незнакомому ей Бобу машину. Боб хочет заплатить чеком, но у Алисы нет способа проверить, действителен ли чек. Алиса хочет, чтобы расчет по чеку был произведен прежде, чем право собственности перейдет к Бобу. Боб, который верит Алисе не больше, чем она ему, не хочет передавать чек, не получив права собственности.
Табл. -1. Действующие лица
| Алиса | Первый участник всех протоколов |
| Боб | Второй участник всех протоколов |
| Кэрол | Третий участник в протоколах с участием трех и четырех сторон |
| Дэйв | Четвертый участник в протоколах с участием трех и четырех сторон |
| Ева | Злоумышленник |
| Мэллори | Взломщик протоколов |
| Трент | Заслуживающий доверия посредник |
| Уолтер | Контролер, защищает Алису и Боба в ряде протоколов |
| Пегги | Свидетель |
| Виктор | Проверяет подлинность |

Рис. -1. Типы протоколов
Посредничество юриста устроит обоих. С его помощью Алиса и Боб могут выполнить следующий протокол, чтобы защитить себя от обмана:
(1) Алиса передает право собственности юристу.
(2) Боб передает чек юристу.
(3) Алиса депонирует чек.
(4) Дождавшись оплаты чека, юрист передает право собственности Бобу. Если чек не оплачен в течение определенного времени, Алиса доказывает этот факт юристу, и тот возвращает право собственности Алисе.
В этом протоколе Алиса верит, что юрист не передаст Бобу право собственности до тех пор, пока чек не будет оплачен, и вернет право собственности Алисе, если чек оплачен не будет. Боб верит, что юрист будет обладать правом собственности до тех пор, пока чек не будет оплачен, и передаст право собственности Бобу сразу же после оплаты чека. Юрист не заботится об оплате чека. Он в любом случае выполнит свою часть протокола, ведь ему заплатят в любом случае.
В этом примере юрист играет роль посредника. Юристы часто выступают в роли посредников при завещаниях и иногда при переговорах о контракте. Различные биржи выступают в качестве посредников между покупателями и продавцами.
Дата добавления: 2021-01-26; просмотров: 546;











