Статистическая совокупность, ее характеристика.

Статистической совокупностью называют группу, состоящую из множества относительно однородных элементов, взятых вместе в известных границах времени и пространства.

Статистическая совокупность состоит из отдельных единичных наблюдений. Численность единиц наблюдения в совокупности определяет объем исследования и обозначается буквой «n».

Каждый первичный элемент, составляющий статистическую совокупность и наделенный признаками сходства, принято называть единицей наблюдения (счетной единицей).

Каждая единица наблюдения имеет несколько признаков, общих для всех единиц, т.е. признаков сходства, позволяющих объединить все элементы в единый объект наблюдения. Помимо признаков сходства каждая единица наблюдения обладает и множеством других признаков, часть из которых может стать предметом изучения, но учитываются только те из них, которые необходимы для достижения поставленной цели и решения конкретных задач исследования. Эти признаки учитывают (регистрируют) и поэтому их называют учитываемыми.

Признаки, по которым различаются элементы статистической совокупности, называют учетными признаками.

Единица наблюдения является носителем признаков, следовательно, эти признаки носят название учетных признаков. Таким образом, учетными признаками, общими для сестринского персонала, - признакам сходства – будут являться:

- профессия (медицинская сестра);

- место работы (конкретное лечебно-профилактическое учреждение).

Учетными признаками, по которым они различаются, являются:

- стаж работы по специальности или в данном медицинском учреждении;

- возраст и т.д.

Такие учитываемые признаки как пол, возраст, место жительства, сроки заболевания и госпитализации, результаты клинических исследований, исходы лечения и другие позволяют всесторонне изучить не только каждый элемент совокупности (единицу наблюдения), но и всю совокупность в целом.

Для оценки изучаемых явлений, составляющих статистическую совокупность, в здравоохранении используют статистические величины: абсолютные числа, относительные и средние величины.

Абсолютные величины могут характеризовать размер изучаемых явлений и процессов. Большое практическое значение для правильного планирования медицинской помощи населению имеют такие абсолютные величины, как численность населения и его отдельных возрастных и половых групп; численность медицинского персонала и лечебно-профилактических учреждений; количество больничных коек и т. д.

Однако, зная только абсолютные данные, мы не можем раскрыть состав, распространенность явления в данной среде. Поэтому в медицинской статистике для характеристики таких явлений, как заболеваемость, смертность, рождаемость и т. д. абсолютные величины переводятся в относительные:интенсивные, экстенсивные показатели, показатели соотношения и наглядности.

Интенсивный показатель –характеризует частоту (распространенность, интенсивность, уровень) явления в среде, в которой оно происходит и с которой непосредственно органически связано. При вычислении интенсивных показателей необходимо знание 2х статистических совокупностей, одна из которых представляет среду, а вторая – явление. Среда продуцирует это явление. Интенсивный показатель может рассчитываться на 100 (%), 1000 (промилле), на 10000 (продецимилле), на 100000 (просантимилле) в зависимости от распространенности явления. Однако в практике здравоохранения существуют общепринятые положения. Так, общая заболеваемость, рождаемость, смертность, младенческая смертность всегда выражается в промилле (‰), а заболеваемость с временной нетрудоспособностью, летальность, частота осложнений рассчитываются на 100 (%).

Методика вычисления интенсивных показателей выглядит следующим образом:

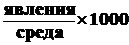
Показатель структуры (экстенсивный) –характеризует распределение явления на составные части, его внутреннюю структуру или отношение частей к целому (удельный вес). При вычислении экстенсивных показателей мы имеем дело только с одной статистической совокупностью и ее составом. Экстенсивный показатель чаще бывает выражен в %, когда за 100 принимается целое явление.

Методика вычисления экстенсивных показателей проста:

В качестве примеров экстенсивных показателей, применяемых в здравоохранении, можно назвать структуру заболеваемости населения; распределение госпитализированных больных по отдельным нозологическим формам, лейкоцитарную формулу и т. д.

Экстенсивными показателями следует пользоваться для характеристики состава совокупности (явления) в данном месте в данное время. Экстенсивные показатели, характеризующие явления, совершаемые в разное время и в различных местностях, сравнивать между собой нельзя, т. к. они не могут характеризовать изменение явления, процесса в динамике.

Показатели наглядности – используются при сравнении однородных явлений, величин. Для этого одну из сравниваемых величин принимают за 100, остальные показываются в виде отношения к этой величине. В показатель наглядности можно преобразовать абсолютные величины, интенсивные показатели, средние величины, представленные как в статике, так и в динамике.

Методика вычисления показателя наглядности:

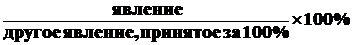
Показатели соотношения характеризуют отношения между разнородными совокупностями. Примером может служить показатель обеспеченности населения больничными койками, врачебными кадрами, средним медперсоналом.

Для облегчения анализа статистического материала, полученные показатели изображают графически. Под графиками понимают условные изображения числовых величин и их соотношений при помощи различных линий, поверхностей и т. п.

При построении графических изображений необходимо соблюдать правила:

- вид графического изображения выбирается в зависимости от статистической величины;

- график строится в определенном масштабе с указанием единицы измерения статических величин;

- каждое графическое изображение должно иметь четкое, ясное, краткое название, отражающее его содержание, и порядковый номер;

- все элементы диаграммы (фигуры, знаки, окраска, штриховка) должны быть пояснены на самой диаграмме или в условных обозначениях (легенде);

- изображаемые графически величины должны иметь цифровые обозначения на самой диаграмме или в прилагаемой таблице.

В медицинской статистике используются диаграммы, картограммы и картодиаграммы.

Экстенсивные показатели, характеризующие структуру явления, изображают в виде секторной или внутристолбиковой диаграммы.

В секторной диаграмме окружность принимается за 100%, при этом 1% соответствует 3,60 окружности. Затем 3,60 умножают на число процентов каждого показателя и получают размер каждого сектора в градусах. При помощи транспортира на окружности откладывают отрезки (отсчет ведется от 00), соответствующие величине каждого показателя. Найденные точки окружности соединяют центром круга. Отдельные секторы круга изображают составные части изучаемого явления.

Вместо секторной диаграммы можно применить внутристолбиковую диаграмму, в которой ширина и высота столбика берутся произвольно. Высота или ширина принимается за 100% и в соответствующем масштабе пересчитываются экстенсивные показатели (в %), составляющие в сумме 100%.

Интенсивные показатели, показатели соотношения и наглядности изображают в виде четырех основных типов диаграмм: линейной, столбиковой, картограммы и картодиаграммы.

Линейная диаграмма применяются для изображения частоты явления, изменяющегося во времени, т. е. изображения динамики явления (динамика численности населения, рождаемости, заболеваемости, смертности, температурная кривая и т. п.). Основой для построения линейной диаграммы является чаще всего прямоугольная система координат. Например, на оси абсцисс х откладывают равные по масштабу промежутки времени, а по оси ординат у – показатели заболеваемости туберкулезом. В тех случаях, когда на одной диаграмме изображено несколько явлений, линии наносят разного цвета или разной штриховки.

Радиальная диаграмма является частным видом линейной диаграммы, построенной на полярных координатах. Изображает динамику явления за замкнутый цикл времени (сутки, неделю, месяц, год и т. д.). Используется при изучении сезонного характера явления (заболеваемость, рождаемость, смертность).

Столбиковаядиаграмма применяется для иллюстрации однородных, но не связанных между собой интенсивных показателей. Ими изображают статику явления: заболеваемость, смертность, инвалидность и т. д. При построении этого вида диаграммы рисуют столбики, высота которых должна соответствовать величине изображаемых показателей с учетом масштаба. Ширина всех столбиков и расстояние между ними должны быть одинаковыми и произвольными. Столбики на диаграмме могут быть вертикальными и горизонтальными (ленточными).

Картограмма –особая географическая карта, на которой отдельные территории заштрихованы с различной интенсивностью соответственно уровню интенсивного показателя. Каждой группе показателей дается условная штриховка или цвет, при этом степень интенсивности штриховки (или окраски) меняется по мере перехода от низких показателей к высоким.

Картодиаграмма– это сочетание географической карты с диаграммой, чаще всего столбиковой: столбики различной величины - соответственно показателю - рисуют на определенных территориях.

Средняя величина – это число, выражающее общую меру исследуемого признака в совокупности.

Различают несколько видов средних величин: мода (Мо), медиана (Ме) и средняя арифметическая (М).

Мода (Мо)- наиболее часто повторяющаяся варианта, т. е. та, которой соответствует наибольшее количество частот (Р) вариационного ряда.

Медиана (Ме)- варианта, занимающая срединное положение в вариационном ряду. При нечетном числе наблюдений для определения медианы надо найти середину ряда – медианой будет центральная (срединная) варианта. При четном числе наблюдений за медиану принимают среднюю величину из двух центральных вариант.

Наиболее часто используется средняя арифметическая величина (М). Она имеет3 основных свойства:

1. Занимает срединное положение в вариационном ряду. В строго симметричном ряду М = Мо = Ме;

2. Имеет абстрактный характер и является обобщающей величиной, вскрывающей то типичное, что характерно для всей совокупности.

3. Алгебраическая сумма отклонений всех вариант от средней равна нулю. Если сумма отклонений вариант от средней равна нулю, то средняя вычислена правильно. На этом свойстве основан расчет средней по способу моментов.

Средняя арифметическая, которая рассчитана в вариационном ряду, где каждая варианта встречается только один раз (для всех вариант р=1), называется средней арифметической простой. Она определяется по формуле:

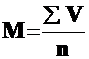где V – значение вариационного признака,

n – общее число наблюдений

Если в исследуемом ряду отдельные варианты встречаются различное число раз (р³1), то вычисляют среднюю арифметическую взвешенную.Расчет ее производится по формуле:

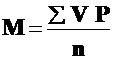где Р – частота, n – сумма частот (å P).