Аналитический метод
Метод применяют в том случае, если ВАХ можно с достаточной степенью точности выразить аналитическими функциями. Для расчете нелинейных электрических цепей также применимы законы Ома и Кирхгофа, однако расчет значительно сложнее, чем для цепей с линейными элементами. Это связаног с тем, что помимо токов и напряжений в нелинейных цепях, неизвестными являются также и сопротивления нелинейных элементов. Если ВАХ нелинейного элемента в некоторых пределах можно заменить прямой линией, то расчет можно свести к расчету линейной цепи.
При расчете нелинейных цепей различают два вида сопротивлений: статическое и дифференциальное (рис.2.2).
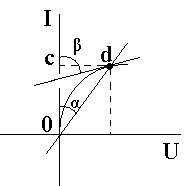
Рис.2.2
Статическоесопротивление в какой то точке d есть отношение напряжения в данной точке (отрезок cd) к току (отрезок 0c):
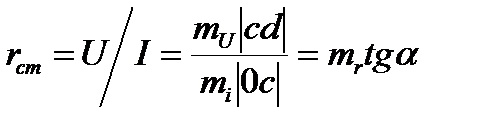 , где mr – масштаб сопротивления.
, где mr – масштаб сопротивления.
Таким образом, статическое сопротивление в какой либо точке d ВАХ пропорционально тангенсу угла α между прямой, соединяющей эту точку dc началом координат и осью токов.
Дифференциальное сопротивление rд – производная от напряжения по току в масштабе mr. Дифференциальное сопротивление пропорционально тангенсу угла β между касательной в данной точке d рассматриваемой характеристики и осью токов:
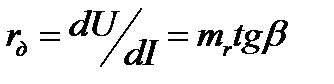
Применяют так же понятие дифференциальной проводимости нелинейного элемента: 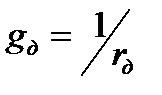
Графический метод
Графический методнаиболее распространен при подборе электронных ламп и полупроводниковых приборов. При этом обычно считают известными ВАХ элементов.
Рассмотрим электрическая цепь с последовательным соединением нелинейных элементов.
ВАХ любого одиночного нелинейного элемента позволяет определить ток при заданном напряжении, и наоборот по заданному току определить напряжение. Поэтому при графическом методе расчета цепи с последовательным соединением нелинейных элементов строят результирующую ВАХ путем суммирования абсцисс характеристик отдельных элементов.
В качестве примера рассмотрим нелинейную цепь (рис. 2.3, а), в которой имеется два последовательно соединенных нелинейных элемента с заданными вольт-амперными характеристиками I(U1)и I(U2)(рис. 2.3,б ,). Так как элементы цепи соединены последовательно, то через них проходит один и тот же ток, а напряжение цепи
U = U1 + U2= Ir1 + Ir2 .(2.1)
Для определения тока I и напряжений U1и U2построим согласно (2.1) результирующую вольт-амперную характеристику I(U).Для построения этой характеристики необходимо просуммировать абсциссы зависимостей I(U1)и I(U2)при различных значениях тока в цепи. Пользуясь результирующей характеристикой, можно непосредственно находить для любого напряжения Uцепи ток и напряжение на нелинейных элементах. Допустим, необходимо по заданному напряжению найти ток в цепи и напряжения на нелинейных элементах с сопротивлениями r1и r2.Если напряжение Uзадано отрезком │0f│,который в масштабе mUравен напряжению U,то, проведя перпендикуляр из точки f до пересечения с кривой I(U)найдем ток в цепи Iв масштабе mI, соответствующий отрезку │fd│.Затем проводим прямую из точки dпараллельно оси абсцисс до пересечения в точкеас осью ординат. Опуская перпендикуляры из точек пересечения bи с прямой daс кривыми I(U1)и I(U2)на ось абсцисс, находим отрезки | 0т| и | 0к|, соответственно равные U1и U2в масштабеmU.
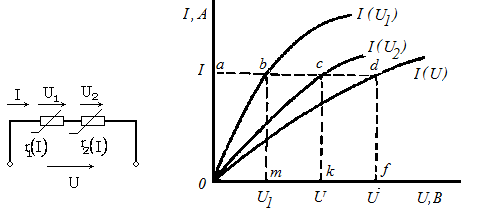
Рис. 2.3
Если задан ток I и требуется найти напряжения U, U1и U2,то по оси ординат откладывают отрезок 0а,равный в масштабе mIтокуI, а затем проводят прямуюad,параллельную оси абсцисс, до пересечения с кривой I(U). Из точек пересечения b,с, dпрямой adс кривыми I(U1), I(U2) и I(U)опускают перпендикуляры на ось абсцисс и находят отрезки 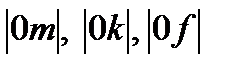 которые в масштабе тцсоответственно равны U1, U2иU.
которые в масштабе тцсоответственно равны U1, U2иU.
Аналогично можно рассчитать графическим путем цепь, состоящую из последовательно соединенных нелинейного и линейного элементов, а также состоящую из большого числа последовательно соединенных нелинейных элементов.
Рассмотрим цепь с параллельным соединением двух нелинейных элементов (рис. 2.4)и с заданными напряжением U и вольт-амперными характеристиками I1(U)и I2(U).По заданным характеристикам I1(U)и I2(U),можно определить токи I1и I2в нелинейных элементах, а затем по первому закону Кирхгофа — ток в неразветвленной части цепи 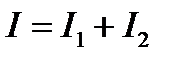 .Нелинейные элементы можно заменить одним с общей характеристикой I(U),которая будет результирующей характеристикой этих элементов.
.Нелинейные элементы можно заменить одним с общей характеристикой I(U),которая будет результирующей характеристикой этих элементов.
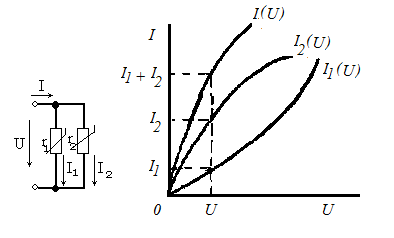
Рис.2.4
Так как при параллельном соединении все элементы цепи находятся под одним напряжением U, то для построения результирующей характеристики I(U)достаточно при различных значениях напряжения Uпросуммировать ординаты вольт-амлерных характеристик отдельных элементов. Как и при последовательном соединении нелинейных элементов, пользуясь вольт-амперными характеристиками, можно найти токи I1, I2 и I по заданному напряжению Uили решить обратную задачу – по заданному току определить напряжение U.
Если параллельно соединены несколько нелинейных элементов, то аналогичным образом можно построить результирующую характеристику цепи. Заметим, что построение результирующей характеристики при параллельном соединении элементов не требуется, если необходимо найти только токи, которые могут быть найдены непосредственно по характеристикам отдельных элементов. Результирующая характеристика при параллельном соединении необходима только тогда, когда требуется по заданному току определить напряжение цепи.
В случае смешанного (рис. 2.5) соединения расчет цепи производят в следующем порядке: сначала заменяют два параллельно соединенных нелинейных элемента одним эквивалентным; схема со смешанным соединением приводится к рассмотренной ранее схеме последовательного соединения двух нелинейных элементов.
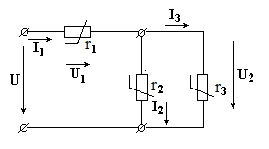
Рис. 2.5
Дата добавления: 2021-01-26; просмотров: 600;











