Восстановление забракованных данных

Исключение из учёта по тем или иным причинам одной или нескольких делянок нарушает сравнимость средних между собой. Так, если выпала делянка в повторении, расположенном на более плодородном участке, то средняя, вычисленная по фактическим данным, будет определена с некоторым недостатком по сравнению со средними вариантов, имевших полное число повторений. И, наоборот, при выпадении делянки повторения с менее плодородного участка средняя этого варианта увеличивается.

Чтобы избежать неравноточности в определении средних вариантов опыта, имеющих забракованные или выпавшие по каким-либо причинам (потрава, смешение урожая, кротовины и т.д.) данные, прибегают к восстановлению, то есть к вычислению наиболее вероятного их значения. Однако следует помнить, что если в пределах одного повторения забракованных данных будет больше 30%, то следует исключить весь этот вариант из последующей статистической обработки. Если в пределах одного повторения выпавших делянок окажется больше 30%, то показатели всех вариантов этого повторения тоже исключаются.

Существует несколько способов вычисления наиболее вероятного значения выпавших дат, различающихся по сложности вычислительных операций, но дающих, в общем, сходные результаты. Применение этих способов основано на допущениях, что:

а) каждое повторение расположено на участке, характеризующемся одинаковым плодородием на всей его территории:

б) все варианты примерно одинаково реагируют на изменение почвенного плодородия.

Если в опыте только одна выпавшая дата, то для её восстановления можно пользоваться формулой Дж. У. Снедекора:

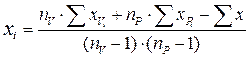(17),

где 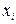– восстановленная дата;

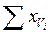– сумма данных того варианта, где находится выпавшее наблюдение;

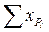– сумма данных того повторения, где находится выпавшее наблюдение;

Если в опыте только одна выпавшая дата, то для её восстановления можно пользоваться формулой Дж. У. Снедекора:

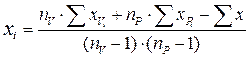(17),

где 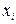– восстановленная дата;

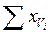– сумма данных того варианта, где находится выпавшее наблюдение;

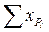– сумма данных того повторения, где находится выпавшее наблюдение;

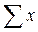– общая сумма поделяночных наблюдений в опыте.

n_Vиn_P – число вариантов и повторений опыта, соответственно.

Таблица 4

Восстановление выпавшего урожая зерна

Вариант	Повторения (х)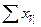
I	II	III	IV
1. Контроль (без удобрений)
2. N60
3. Р60
4. N60P60
5. N60P60K60

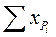
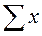
Несколько данных в одном опыте рекомендуется восстанавливать по формуле, предложенной А.С. Молостовым (:

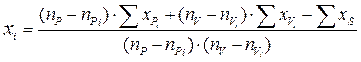(18),

где 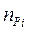– число повторений с выпавшими данными в том варианте, где проводится восстановление;

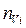– число вариантов с выпавшими данными;

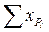– сумма поделяночных данных одного повторения за вычетом тех вариантов, где имеются выпавшие данные;

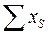– сумма поделяночных данных всех вариантов с полным набором делянок тех повторений, в которых не выпали поделяночные урожаи того варианта, для которого восстанавливают урожаи.

В качестве примера рассмотрим результаты экологического опыта, целью которого было изучение влияния приближённости посевов яровой пшеницы к автомагистрали на накопление свинца в зерне. Опыт включал 6 вариантов, был заложен в 6 повторностях. Шаг удалённости от автомагистрали – 50 м. Методом выбраковки данных были ликвидированы 3 даты: вариант 60 метров от трассы четвёртого повторения, вариант 160 метров от трассы 3 повторения и вариант 210 метров от трассы шестого повторения. Для восстановления выпавших дат была составлена следующая матрица (табл. 5).

Таблица 5

Вычисление выпавших концентраций свинца в зерне яровой пшеницы по данным экологического опыта

Вариант, удаление от трассы, м	Содержание свинца в зерне пшеницы по повторениям, мг/кг сухой массы	Сумма
I	II	III	IV	V	VI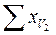
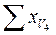
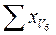
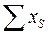
	34,5	30,2	32,4	35,1	29,6	32,2
	17,5	15,3	15,0	–	12,8	13,5	74,1			242,82
	9,4	12,5	8,6	11,5	10,4	9,2
	8,5	9,0	–	8,2	7,1	9,7		42,5		248,63
	6,0	8,4	7,0	7,2	6,5	5,9
	5,4	7,8	7,0	6,9	6,4	–			33,5	249,34
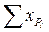
	49,91	51,1	48,0	53,8	46,5	47,3

¹ 49,9 = 34,5+9,4+6,0

² 242,8 = 49,9+51,1+48,0+46,5+47,3

³ 248,6 = 49,9+51,1+53,8+46,5+47,3

⁴ 249,3 = 49,9+51,1+48,0+53,8+46,5

Подставляя в формулу соответствующие числовые значения, получим:

для делянки второго варианта четвёртого повторения:

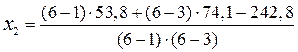= 16,6 мг/кг

для делянки четвёртого варианта третьего повторения:

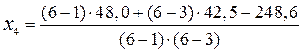= 7,9 мг/кг

для делянки шестого варианта шестого повторения:

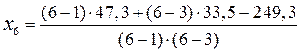= 5,8 мг/кг.

Следует помнить, что при дальнейших расчётах при оценке точности опыта необходимо будет учитывать тот факт, что данные были восстановлены, поэтому следует восстановленные даты заключать в квадратные скобки.