ВОЗМОЖНОСТИ ПРОГРАММНОГО КОМПЛЕКСА NX

Рис. 1.1. Схема осевого растяжения ступенчатого стержня

Разобьем стержень на два элемента площадью поперечного сечения А1 и А2 соответственно и введем на границах элементов узлы 1, 2 и 3. Из уравнений равновесия стержня можно получить зависимости для расчета перемещений узлов [3]:

,

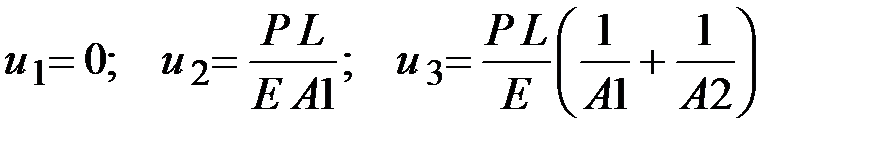где Е – модуль упругости материала стержня, Па; Р – осевая сила, Н; А1 и А2 – площади поперечных сечений элементов, м²; L – длина стержней, м.

При построении дискретных аналогов дифференциальных уравнений теплопроводности используют универсальный метод баланса. Для каждого типа расчетных элементов изучаемых объектов (заготовки, стружки, инструмента) методом баланса получают дискретные аналоги соответствующих дифференциальных уравнений теплопроводности. Каждому расчетному элементу присваивают уникальный двухкомпонентный номер i, j, в котором i – номер расчетной точки в направлении оси 0x (рис. 1.2); j – то же в направлении оси 0y (при решении двухмерной задачи).

Из закона сохранения энергии следует, что сумма всех входящих и выходящих за время Δτ тепловых потоков (см. рис. 1.2) равна изменению энтальпии рассматриваемого элемента (конечного объема):

,

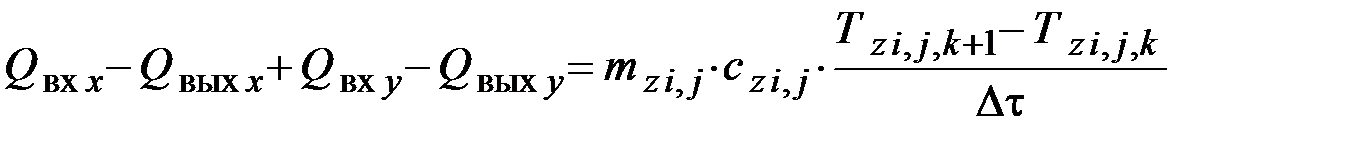где Q_{вх х}, Q_{вых х} – тепловой поток, соответственно входящий в элемент (i, j) и выходящий из него в направлении оси 0х, Вт; Q_{вх у}, Q_{вых у} – то же в направлении оси 0у; 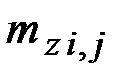– масса расчетного элемента, кг; 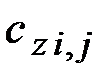– удельная теплоемкость объекта, Дж/(кг · К); 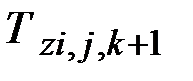– температура расчетного элемента объекта в рассматриваемый момент времени, К; 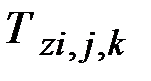– то же в предыдущий момент времени, К; z – номер рассматриваемого объекта; подстрочный индекс, содержащий двухкомпонентный номер расчетного элемента, обозначает принадлежность соответствующего параметра к этому расчетному элементу.

Составляющие теплового баланса определяются следующими зависимостями:

,

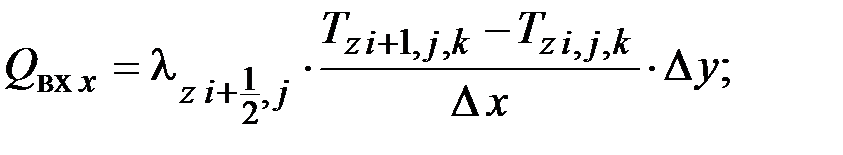
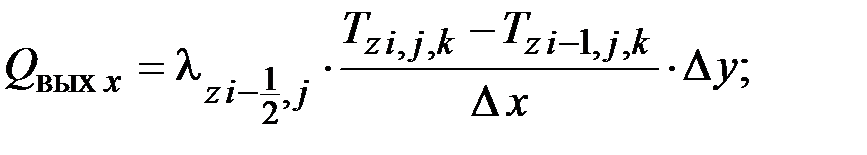
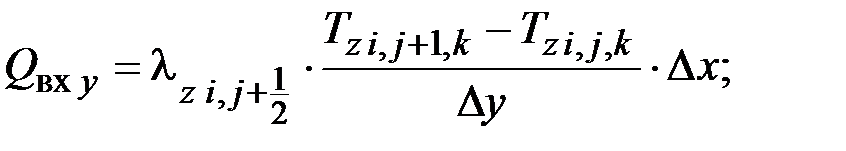
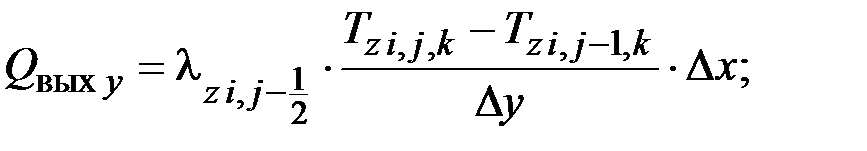
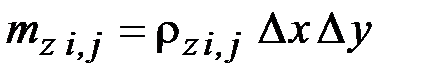где 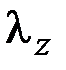– теплопроводность z-го объекта, Вт/(м·К); Δх, Δу – расстояние между расчетными точками в направлении оси 0х и 0у соответственно, м.

Qвых у

(i, j – 1)

(i, j)

(i – 1, j)

Qвых х

Qвх х

(i + 1, j)

Qвх y

(i, j + 1)

Рис. 1.2. Баланс теплоты типового расчетного элемента: – расчетные точки, задействованные в тепловом балансе; Qвх х, Qвых х – тепловой поток, соответственно входящий в элемент (i, j) и выходящий из него в направлении оси 0х; Qвх у, Qвых у – то же в направлении оси 0у

Дискретный аналог уравнения теплопроводности z-го объекта для типового расчетного элемента с внутренней расчетной точкой:

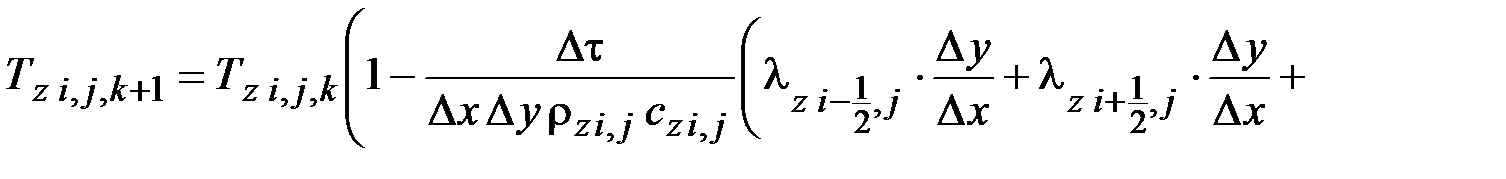
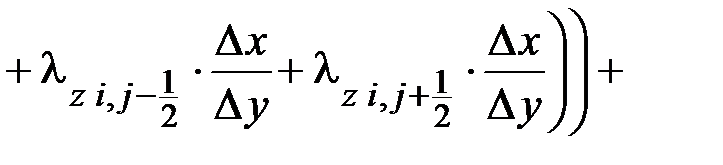
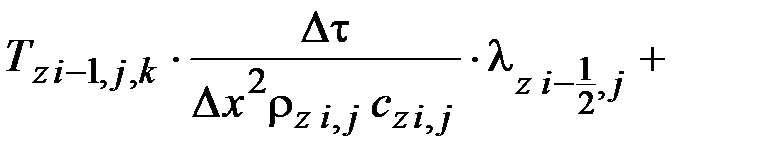
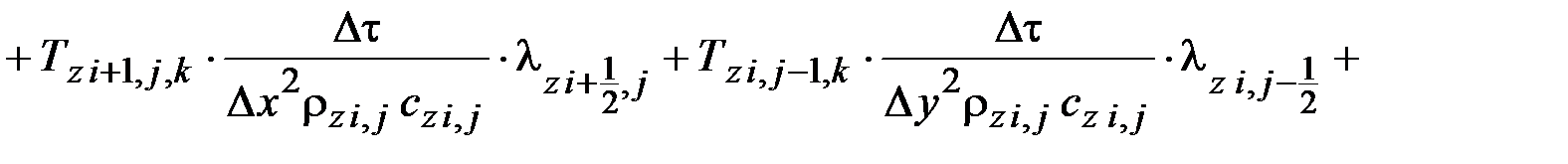
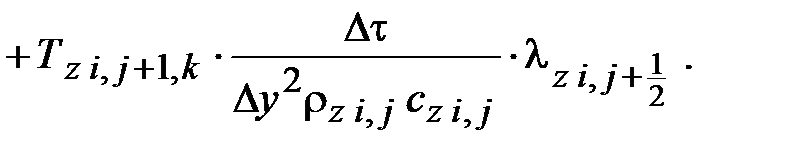
Дискретные аналоги дифференциальных уравнений теплопроводности для остальных расчетных элементов зон контакта объектов и на их поверхностях получают аналогично.

Вышеприведенные зависимости определяют физико-механичес-кие характеристики материала изучаемого объекта, используемые в качестве исходных данных для решения задач, размеры сетки конечных элементов, в частности параметры А1, А2, Δх, Δу (см. подраздел 2.3), а также условия нагрузки объекта (см. подраздел 2.4).

ВОЗМОЖНОСТИ ПРОГРАММНОГО КОМПЛЕКСА NX