Основные закономерности движения ИСЗ
Искусственный спутник Земли (ИСЗ) → искусственно созданное небесное тело, обращающееся вокруг Земли только под действием силы ее притяжения, без участия каких-либо других сил.
Для движения ИСЗ по орбите необходимо, чтобы сила земного притяжения была скомпенсирована центробежной силой, возникающей при движении ИСЗ относительно центра Земли. Это условие приводит к равенству:
| m · g = m · ρ0 · ωC2 | (23.1) |
| где | m – масса ИСЗ; |
| g – ускорение свободного падения; | |
| ρ0 = R + H – радиус орбиты ИСЗ (расстояние до ИСЗ от центра Земли); | |
| ωC – угловая скорость ИСЗ относительно центра Земли. |
Так как
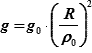
| (23.2) |
а
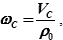
| (23.3) |
то формула (23.1) для линейной скорости (Vc) ИСЗ на круговой орбите примет вид:
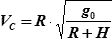
| (23.4) |
Подставив в формулу (23.4): 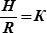 , R = 6371 км, g0 = 9,80665м/с2 ≈ 9,81м/с2 – получим:
, R = 6371 км, g0 = 9,80665м/с2 ≈ 9,81м/с2 – получим:
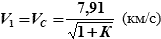
| (23.5) |
Скорость, при которой начинается движения ИСЗ по окружности вокруг Земли, называется круговой или первой космической скоростью. При Н = 0 → V1 = 7,91 км/с.
Период обращения ИСЗ вокруг Земли определяется по формуле:
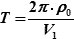
| (23.6) |
В зависимости от высоты орбиты (Н) и значения скорости ИСЗ (V1) и его период (Т) различны (см. табл. 23.1):
Зависимость периода обращения и скорости ИСЗ от высоты его орбиты
Таблица 23.1.
| Н, км | |||||
| Т, мин. | 12 час | 24 час | |||
| V1, км/с | 7,91 | 7,76 | 7,35 | 3,87 | 3,07 |
Периодические (синхронные) ИСЗ – это такие ИСЗ, которые за время звездных суток делают целое число оборотов (пролетают над районом судна ежедневно в одно и то же время).
Синхронный ИСЗ на орбите с Н = 35.870 км имеет Т = 24 часа (23ч 56м 4с – одни звездные сутки) называется суточным. Такие ИСЗ используются в системах связи и телевидения.
В общем случае орбита ИСЗ является не круговой, а эллиптической, которая характеризуется большой (а) и малой (в) полуосью эллипса.
Перигей (П) – ближайшая к центру Земли точка орбиты; апогей (А) – наиболее удаленная точка орбиты ИСЗ от центра Земли.
Эллиптическая орбита характеризуется 6-ю элементами Кеплера (рис. 23.1):
1. → наклонение плоскости орбиты к плоскости экватора (i) → угол между плоскостью земного экватора и плоскостью орбиты ИСЗ;
2. → прямое восхождение восходящего узла орбиты (Ω) → угол между направлениями на точку Овна и восходящий узел орбиты ИСЗ;
3. → угловое расстояние перигея от восходящего узла орбиты N (ω) → угол между направлениями на восходящий узел орбиты ИСЗ и точку его перигея;
4. → эксцентриситет орбиты (е):
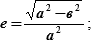
| (23.7) |
5. → параметр орбиты:
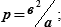
| (23.8) |
6. → время прохождения ИСЗ через перигей (П) или восходящий (N) узел (τ).
Элементы №№ 1÷5 характеризуют пространственное положение орбиты ИСЗ и направление его движения.
Элемент № 6 (τ) – характеризует положение ИСЗ на орбите.
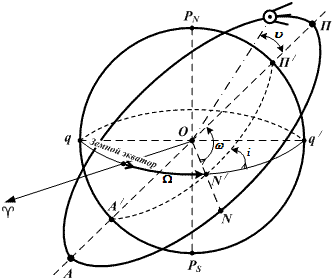
Рис. 23.1. Характеристика эллиптической орбиты ИСЗ
Для определения места судна по ИСЗ необходимо знать его координаты в момент наблюдений.
По известным значениям параметров орбиты ИСЗ можно вычислить его пространственные координаты и положение его относительно земной поверхности на любой момент времени.
Мгновенное положение ИСЗ относительной земной поверхности можно определить длиной радиуса-вектора его орбиты
| ρ0 = R + H | (23.9) |
и координатами геозенита – точки на земной поверхности, для которой ИСЗ в данный момент находится в зените.
В геометрической интерпретации именно точка геозенита является опорным пунктом, относительно которого определяются навигационные параметры.
Вследствие того, что Земля не шар, а геоид и того, что на ИСЗ влияет ряд возмущающих сил (сопротивление атмосферы Земли, притяжение Луны и Солнца, давление солнечной радиации, магнитное поле Земли), кеплеровские элементы орбиты ИСЗ непрерывно изменяются.
Для исключения этого на все суда, использующие ИСЗ, сообщаются не только начальные параметры элементов Кеплера, но и действительные поправки к ним (орбитальная информация).
Дата добавления: 2021-01-26; просмотров: 677;











