Ячейки памяти и их адреса.

<2 3 456 7 8 >

Память - часть компьютера, где хранятся программы и данные. Можно также употреблять термин «запоминающее устройство». Без памяти, откуда процессоры считывают и куда записывают информацию, не было бы цифровых компьютеров со встроенными программами.

1.1.Бит

Основной единицей памяти является двоичный разряд, который называется битом. Бит может содержать 0 или 1. Эта самая маленькая единица памяти. (Устройство, в котором хранятся только нули, вряд ли могло быть основой памяти. Необходимы по крайней мере две величины.) Многие полагают, что в компьютерах используется бинарная арифметика, потому что это «эффективно». Они имеют в виду (хотя сами это редко осознают),

что цифровая информация может храниться благодаря различию между разными величинами какой-либо физической характеристики, например напряжения или тока. Чем больше величин, которые нужно различать, тем меньше различий между смежными величинами и тем менее надежна память. Двоичная система требует различения всего двух величин, следовательно, это самый надежный метод кодирования цифровой информации. Если вы не знакомы с двоичной системой счисления, смотрите Приложение А.

Считается, что некоторые компьютеры, например большие IBM, используют и десятичную, и двоичную арифметику. На самом деле здесь применяется так называемый двоично-десятичный код. Для хранения одного десятичного разряда используется 4 бита. Эти 4 бита дают 16 комбинаций для размещения 10 различных значений (от 0 до 9). При этом 6 оставшихся комбинаций не используются. Ниже показано число 1944 в двоично-десятичной и чисто двоичной системах счисления; в обоих случаях используется 16 битов:

десятичное: 0001 10010100 0100 двоичное: 0000011110011000

16 битов в двоично-десятичном формате могут хранить числа от 0 до 9999, то есть всего 10000 различных комбинаций, а 16 битов в двоичном формате — 65536 комбинаций. Именно по этой причине говорят, что двоичная система эффективнее.

Однако представим, что могло бы произойти, если бы какой-нибудь гениаль-

ный молодой инженер придумал очень надежное электронное устройство, которое могло бы хранить разряды от 0 до 9, разделив участок напряжения от 0 до 10 В на 10 интервалов. Четыре таких устройства могли бы хранить десятичное число от 0 до 9999, то есть 10 000 комбинаций. А если бы те же устройства использовались для хранения двоичных чисел, они могли бы содержать всего 16 комбинаций. Естественно, в этом случае десятичная система была бы более эффективной.

1.2.Адреса памяти

Память состоит из ячеек, каждая из которых может хранить некоторую порцию информации. Каждая ячейка имеет номер, который называется адресом, По адресу программы могут ссылаться на определенную ячейку. Если память содержит п ячеек, они будут иметь адреса от 0 до п-1. Все ячейки памяти содержат одинаковое число битов. Если ячейка состоит из к битов, она может содержать любую из 2к комбинаций. На рис. 2.8 показаны 3 различных способа организации 96-битной памяти. Отметим, что соседние ячейки по определению имеют последовательные адреса.

В компьютерах, где используется двоичная система счисления (включая восьмеричное и шестнадцатеричное представление двоичных чисел), адреса памяти также выражаются в двоичных числах. Если адрес состоит из m битов, максимальное число адресованных ячеек будет составлять 2П|. Например, адрес для обращения к памяти, изображенной на рис. 2.8, а, должен состоять, по крайней мере, из 4 битов, чтобы выражать все числа от 0 до 11. При устройстве памяти, показанном на рис. 2.8, 6 и 2.8, в, достаточно 3-битного адреса. Число битов в адресе определяет максимальное количество адресованных ячеек памяти и не зависит от числа битов в ячейке. 12-битные адреса нужны и памяти с 212 ячеек по 8 битов каждая, и памяти с 212 ячеек по 64 бита каждая.

В табл. 2.1 показано число битов в ячейке для некоторых коммерческих компьютеров.

Ячейка - минимальная единица, к которой можно обращаться, В последние

годы практически все производители выпускают компьютеры с 8-битными ячейками, которые называются байтами, Байты группируются в слова. Компьютер с 32-битными словами имеет 4 байта на каждое слово, а компьютер с 64-битными словами — 8 байтов на каждое слово. Такая единица, как слово, необходима, поскольку большинство команд производят операции над целыми словами (например, складывают два слова). Таким образом, 32-битная машина будет содержать 32-битные регистры и команды для манипуляций с 32-битными словами, тогда как 64-битная машина будет иметь 64-битные регистры и команды для перемещения, сложения, вычитания и других операций над 64-битными словами.

1.3.Упорядочение байтов

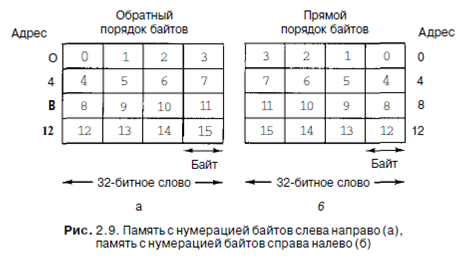
Байты в слове могут нумероваться слева направо или справа налево. На первый взгляд может показаться, что между этими двумя вариантами нет разницы, но мы скоро увидим, что выбор имеет большое значение. На рис. 2.9, а изображена часть памяти 32-битного компьютера, в котором байты пронумерованы слева направо (как у компьютеров SPARC или больших IBM). Рисунок 2.9,6 показывает аналогичную репрезентацию 32-битного компьютера с нумерацией байтов справа налево (как у компьютеров Intel).

Важно понимать, что в обеих системах 32-битное целое число (например, 6)

представлено битами 110 в трех крайних правых битах слова, а остальные 29 битов представлены нулями. Если байты нумеруются слева направо, биты 110 находятся в байте 3 (или 7, или 11 и т. д.). Если байты нумеруются справа налево, биты 110 находятся в байте 0 (или 4, или 8 и т. д.). В обоих случаях слово, содержащее это целое число, имеет адрес 0.

Если компьютеры содержат только целые числа, никаких сложностей не возникает. Однако многие прикладные задачи требуют использования не только целых чисел, но и цепочек символов и других типов данных. Рассмотрим, например, простую запись данных персонала, состоящую из цепочки символов (имя сотрудника) и двух целых чисел (возраст и номер отдела). Цепочка символов завершается одним или несколькими байтами 0, чтобы заполнить слово. На рис. 2.10, а представлена схема с нумерацией байтов слева направо, а на рис. 2.10, б - с нумерацией байтов

справа налево для записи «Jim Smith, 21 год, отдел 260» (1x256+4=260).

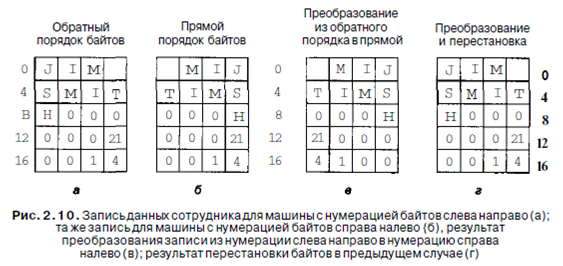
Оба эти представления хороши и внутренне последовательны. Проблемы начинаются тогда, когда один из компьютеров пытается переслать эту запись на Другой компьютер по сети. Предположим, что машина с нумерацией байтов слева направо пересылает запись на компьютер с нумерацией байтов справа налево по одному байту, начиная с байта 0 и заканчивая байтом 19. Для простоты будем считать, что биты, не инвертируются при передаче. Таким образом, байт 0 переносится из первой машины на вторую в байт 0 и т. д., как показано на рис. 2.10, в.

Компьютер, получивший запись, имя печатает правильно, но возраст получа-

ется 21х224, и номер отдела тоже искажается. Такая ситуация возникает, поскольку при передаче записи порядок букв в слове меняется так, как нужно, но при этом порядок байтов целых чисел тоже изменяется, что приводит к неверному результату.

Очевидное решение этой проблемы - наличие программного обеспечения, которое инвертировало бы байты в слове после того, как сделана копия. Результат такой операции изображен на рис. 2.10, г. Мы видим, что числа стали правильными, но цепочка символов превратилась в «MIJTIMS», при этом «Н» вообще поместилась отдельно. Цепочка переворачивается потому, что компьютер сначала считывает байт 0 (пробел), затем байт 1 (М) и т. д.

Простого решения не существует. Есть один способ, но он неэффективен. (Нужно перед каждой единицей данных помещать заголовок, информирующий, какой тип данных последует за ним — цепочка, целое число и т. д. Это позволит компьютеру-получателю производить только необходимые преобразования.) Ясно, что отсутствие стандарта упорядочивания байтов является главным неудобством при обмене информацией между разными машинами.

1.4.Код с исправлением ошибок

Память компьютера время от времени может делать ошибки из-за всплесков напряжения на линии электропередачи и по другим причинам. Чтобы бороться с такими ошибками, используются коды с обнаружением и исправлением ошибок. При этом к каждому слову в памяти особым образом добавляются дополнительные биты. Когда слово считывается из памяти, эти биты проверяются на наличие ошибок. Чтобы понять, как обращаться с ошибками, необходимо внимательно изучить, что представляют собой эти ошибки. Предположим, что слово состоит из m битов данных, к которым мы прибавляем г дополнительных битов (контрольных разрядов).

Пусть общая длина слова будет п (то есть п=т+г). n-битную единицу, содержащую m битов данных и г контрольных разрядов, часто называют кодированным словом. Для любых двух кодированных слов, например 10001001 и 10110001, можно определить, сколько соответствующих битов в них различается. В данном примере таких бита три. Чтобы определить количество различающихся битов, нужно над двумя кодированными словами произвести логическую операцию ИСКЛЮЧАЮЩЕЕ ИЛИ и сосчитать число битов со значением 1 в полученном результате. Число битовых позиций, по которым различаются два слова, называется интервалом Хэмминга. Если интервал Хэмминга для двух слов равен d, это значит, что достаточно d битовых ошибок, чтобы превратить одно слово в другое. Например, интервал Хэмминга кодированных слов 11110001 и 00110000 равен 3, поскольку для превращения первого слова во второе достаточно 3 ошибок в битах.

Память состоит из m-битных слов, и следовательно, существует 2т вариантов

сочетания битов. Кодированные слова состоят из п битов, но из-за способа подсчета контрольных разрядов допустимы только 2Ш из 2" кодированных слов. Если в памяти обнаруживается недопустимое кодированное слово, компьютер знает, что произошла ошибка. При наличии алгоритма для подсчета контрольных разрядов можно составить полный список допустимых кодированных слов и из этого списка найти два слова, для которых интервал Хэмминга будет минимальным. Это интервал Хэмминга полного кода.

Свойства проверки и исправления ошибок определенного кода зависят от его

интервала Хэмминга. Чтобы обнаружить d ошибок в битах, необходим код с интервалом d+1, поскольку d ошибок не могут изменить одно допустимое кодированное слово на другое допустимое кодированное слово Соответственно, чтобы исправить d ошибок в битах, необходим код с интервалом 2d+l, поскольку в этом случае допустимые кодированные слова так сильно отличаются друг от друга, что даже если произойдет d изменений, изначальное кодированное слово будет ближе к ошибочному, чем любое другое кодированное слово, поэтому его без труда можно будет определить.

В качестве простого примера кода с обнаружением ошибок рассмотрим код, в котором к данным присоединяется один бит четности. Бит четности выбирается таким образом, что число битов со значением 1 в кодированном слове четное (или нечетное). Интервал этого кода равен 2, поскольку любая ошибка в битах приводит к кодированному слову с неправильной четностью. Другими словами, достаточно двух ошибок в битах для перехода от одного допустимого кодированного слова к другому допустимому слову. Такой код может использоваться для обнаружения одиночных ошибок. Если из памяти считывается слово, содержащее неверную четность, поступает сигнал об ошибке. Программа не сможет продолжаться, но зато не будет неверных результатов. В качестве простого примера кода с исправлением ошибок рассмотрим код с четырьмя допустимыми кодированными словами:

0000000000,0000011111, ШИОООООи 1111111111

Интервал этого кода равен 5. Это значит, что он может исправлять двойные

ошибки. Если появляется кодированное слово 0000000111, компьютер знает, что изначальное слово должно быть 0000011111 (если произошло не более двух ошибок). При наличии трех ошибок, если, например, слово 0000000000 изменилось на 0000000111, этот метод недопустим.

Представим, что мы хотим разработать код с m битами данных и г контрольных разрядов, который позволил бы исправлять все ошибки в битах. Каждое из 2т допустимых слов имеет п недопустимых кодированных слов, которые отличаются от допустимого одним битом. Они образуются инвертированием каждого из п битов в n-битном кодированном слове. Следовательно, каждое из 2т допустимых слов требует п+1 возможных сочетаний битов, приписываемых этому слову (п возможных ошибочных вариантов и один правильный). Поскольку общее число различных сочетаний битов равно 2П, то (п+1)2га<2п. Так как n-ш+г, следовательно,

(т+г+ 1)<2Г. Эта формула дает нижний предел числа контрольных разрядов, необходимых для исправления одиночных ошибок. В табл 2.2 показано необходимое количество контрольных разрядов для слов разного размера.

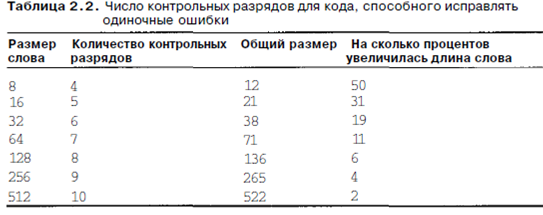
Этого теоретического нижнего предела можно достичь, используя метод Ричарда Хэмминга. Но прежде чем обратиться к этому алгоритму, давайте рассмотрим простую графическую схему, которая четко иллюстрирует идею кода с исправлением ошибок для 4-битных слов. Диаграмма Венна на рис. 2.11 содержит 3 круга, А, В и С, которые вместе образуют семь секторов. Давайте закодируем в качестве примера слово из 4 битов 1100 в сектора АВ, ABC, AC и ВС, по одному биту в каждом секторе (в алфавитном порядке). Кодирование показано на рис. 2.11, а.

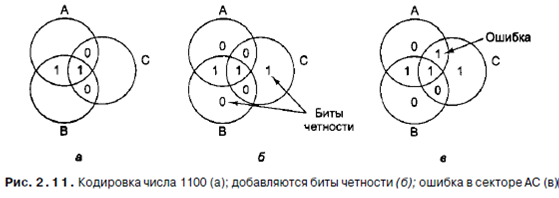
Далее мы добавим бит четности к каждому из трех пустых секторов, чтобы получилась положительная четность, как показано на рис. 2.11, б. По определению сумма битов в каждом из трех кругов, А, В, и С, должна быть четной. В круге А находится 4 числа: 0, 0, 1 и 1, которые в сумме дают четное число 2. В круге В находятся числа 1, 1, 0 и 0, которые также при сложении дают четное число 2. То же имеет силу и для круга С. В данном примере получилось так, что все суммы одинаковы, но вообще возможны случаи с суммами 0 и 4. Рисунок соответствует кодированному слову, состоящему из 4 битов данных и 3 битов четности. Предположим, что бит в секторе АС изменился с 0 на 1, как показано на рис. 2.11, в. Компьютер видит, что круги А и С имеют отрицательную четность. Единственный способ исправить ошибку, изменив только один бит, -возвраще-

ние биту АС значения 0. Таким способом компьютер может исправлять одиночные ошибки автоматически.

А теперь посмотрим, как может использоваться алгоритм Хэмминга при создании кодов с исправлением ошибок для слов любого размера. В коде Хэмминга к слову, состоящему из m битов, добавляется г битов четности, при этом образуется слово длиной т+г битов. Биты нумеруются с единицы (а не с нуля), причем первым считается крайний левый. Все биты, номера которых — степени двойки, являются битами четности; остальные используются для данных. Например, к 16-битному слову нужно добавить 5 битов четности. Биты с номерами 1, 2, 4, 8 и 16 — биты четности, а все остальные — биты данных. Всего слово содержит 21 бит (16 битов данных и 5 битов четности). В рассматриваемом примере мы будем использовать

положительную четность (выбор произвольный). Каждый бит четности проверяет определенные битовые позиции. Общее число битов со значением 1 в проверяемых позициях должно быть четным. Ниже указаны позиции проверки для каждого бита четности:

Бит 1 проверяет биты 1, 3, 5,7, 9,11, 13,15,17,19, 21.

Бит 2 проверяет биты 2, 3, 6, 7,10,11,14,15,18,19.

Бит 4 проверяет биты 4, 5,6, 7,12,13,14,15, 20, 21.

Бит 8 проверяет биты 8,9,10, И, 12,13,14, 15.

Бит 16 проверяет биты 16,17,18,19, 20, 21.

В общем случае бит b проверяется битамиЪи Ь2,..., bJt такими что bi+b2+... +b,=b. Например, бит 5 проверяется битами 1 и 4, поскольку 1+4=5. Бит 6 проверяется битами 2 и 4, поскольку 2+4=6 и т. д.

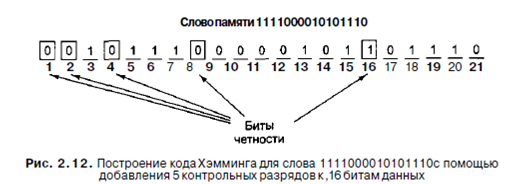
На рис. 2.12 показано построение кода Хэмминга для 16-битного слова

1111000010101110 Соответствующим 21-битным кодированным словом является 001011100000101101110. Чтобы увидеть, как происходит исправление ошибок, рассмотрим, что произойдет, если бит 5 изменит значение из-за резкого скачка напряжения на линии электропередачи. В результате вместо кодированного слова 001011100000101101110 получится 001001100000101101 ПО. Будут проверены 5 битов четности.

Вот результаты проверки:

Бит четности 1 неправильный (биты 1, 3, 5, 7,9, 11, 13, 15, 17, 19, 21 содержат

пять единиц).

Бит четности 2 правильный (биты 2, 3, 6,7,10,11,14,15,18,19 содержат шесть

единиц).

Бит четности 4 неправильный (биты 4,5,6,7,12,13,14,15,20,21 содержат пять

единиц).

Бит четности 8 правильный (биты 8,9,10,11,12,13,14,15 содержат две единицы).

Битчетности 16 правильный (биты 16,17,18,19,20,21 содержат четыре единицы).

Общее число единиц в битах 1, 3, 5, 7, 9, 11, 13, 15, 17, 19 и 21 должно быть

четным, поскольку в данном случае используется положительная четность. Неправильным должен быть один из битов, проверяемых битом четности 1 (а именно 1,3,5,7,9,11,13,15,17,19 и 21). Бит четности 4 тоже неправильный. Это значит, чтоизменил значение один из следующих битов: 4,5,6,7,12,13,14,15,20,21. Ошибка должна быть в бите, который содержится в обоих списках. В данном случае общими являются биты 5,7,13,15 и 21. Поскольку бит четности 2 правильный, биты 7 и 15 исключаются. Правильность бита четности 8 исключает наличие ошибки в бите 13.

Наконец, бит 21 также исключается, поскольку бит четности 16 правильный. В итоге остается бит 5, в котором и содержится ошибка. Поскольку этот бит имеет значение 1, он должен принять значение 0. Именно таким образом исправляются ошибки.

Чтобы найти неправильный бит, сначала нужно подсчитать все биты четности. Если они правильные, ошибки нет (или есть, но больше одной). Если обнаружились неправильные биты четности, то нужно сложить их номера. Сумма, полученная в результате, даст номер позиции неправильного бита. Например, если биты четности 1 и 4 неправильные, а 2,8 и 16 правильные, то ошибка произошла в бите 5 (1+4).

2.Кэш-память

Процессоры всегда работали быстрее, чем память. Процессоры и память совершенствовались параллельно, поэтому это несоответствие сохранялось. Поскольку на микросхему можно помещать все больше и больше транзисторов, разработчики процессоров использовали эти преимущества для создания конвейеров и суперскалярной архитектуры, что еще больше повышало скорость работы процессоров. Разработчики памяти обычно использовали новые технологии для увеличения емкости, а не скорости, что еще больше усугубляло проблему. На практике такое несоответствие в скорости работы приводит к следующему: после того как процессор дает запрос памяти, должно пройти много циклов, прежде чем он получит слово,

которое ему нужно. Чем медленнее работает память, тем дольше процессору приходится ждать, тем больше циклов должно пройти.

Как мы уже говорили выше, есть два пути решения этой проблемы. Самый простой из них — начать считывать информацию из памяти, когда это необходимо, и при этом продолжать выполнение команд, но если какая-либо команда попытается использовать слово до того, как оно считалось из памяти, процессор должен приостанавливать работу. Чем медленнее работает память, тем чаще будет возникать такая проблема и тем больше будет проигрыш в работе. Например, если отсрочка составляет 10 циклов, весьма вероятно, что одна из 10 следующих команд попытается использовать слово, которое еще не считалось из памяти.

Другое решение проблемы - сконструировать машину, которая не приостанавливает работу, но следит, чтобы программы-компиляторы не использовали слова до того, как они считаются из памяти. Однако это не так просто осуществить на практике. Часто при выполнении команды загрузки машина не может выполнять другие действия, поэтому компилятор вынужден вставлять пустые команды, которые не производят никаких операций, но при этом занимают место в памяти. В действительности при таком подходе простаивает не аппаратное, а программное обеспечение, но снижение производительности при этом такое же. На самом деле эта проблема не технологическая, а экономическая. Инженеры знают, как построить память, которая будет работать так же быстро, как и процессор, но при этом ее приходится помещать прямо на микросхему процессора (поскольку информация через шину поступает очень медленно). Установка большой памяти на микросхему процессора делает его больше и, следовательно, дороже, и даже если бы стоимость не имела значения, все равно существуют ограничения в размерах процессора, который можно сконструировать. Таким образом, приходится выбирать между быстрой памятью небольшого размера и медленной памятью большого размера. Мы бы предпочли память большого размера с высокой скоростью работы по низкой цене. Интересно отметить, что существуют технологии сочетания маленькой и быстрой памяти с большой и медленной, что позволяет получить и высокую скорость работы, и большую емкость по разумной цене. Маленькая память с высокой скоростью работы называется кэш-памятью (от французского слова cacher «прятать»1;читается «кэш»). Ниже мы кратко опишем, как используется кэш-память и как она работает. Более подробное описание см. в главе 4. Основная идея кэш-памяти проста: в ней находятся слова, которые чаще всего используются. Если процессору нужно какое-нибудь слово, сначала он обращается к кэш-памяти. Только в том случае, если слова там нет, он обращается к основной памяти. Если значительная часть слов находится в кэш-памяти, среднее время доступа значительно сокращается. Таким образом, успех или неудача зависит от того, какая часть слов находится в кэш-памяти. Давно известно, что программы не обращаются к памяти наугад. Если программе нужен доступ к адресу А, то скорее всего после этого ей понадобится доступ к адресу, расположенному поблизости от А. Практически все команды обычной программы (за исключением команд перехода и вызова процедур) вызываются из последовательных участков памяти. Кроме того, большую часть времени программа тратит на циклы, когда ограниченный набор команд выполняется снова и снова. Точно так же при манипулировании матрицами программа, скорее всего, будет обращаться много раз к одной и той же матрице, прежде чем перейдет к чему-либо другому. То, что при последовательных отсылках к памяти в течение некоторого промежутка времени используется только небольшой ее участок, называется принципом локальности. Этот принцип составляет основу всех систем кэш-памяти. Идея состоит в следующем: когда определенное слово вызывается из памяти, оно вместе с соседними словами переносится в кэш-память, что позволяет при очередном запросе быстро обращаться к следующим словам. Общее устройство процессора, кэш-памяти и основной памяти показано на рис. 2.13. Если слово считывается или записывается к раз, компьютеру понадобится сделать 1 обращение к медленной основной памяти и к-1 обращений к быстрой кэш-памяти. Чем больше к, тем выше общая производительность.

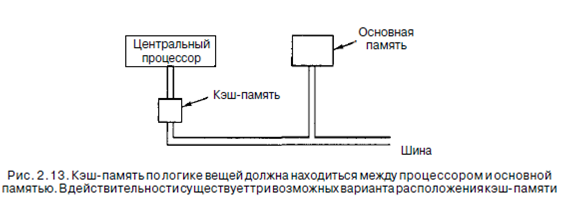
Мы можем сделать более строгие вычисления. Пусть с - время доступа к кэш-памяти, m - время доступа к основной памяти и h - коэффициент совпадения, который показывает соотношение числа ссылок к кэш-памяти и общего числа всех ссылок. В нашем примере h=(k~l)/k. Таким образом, мы можем вычислить среднее время доступа:

среднее время доступа =с+( 1 -h)m.

Если h—И и все обращения делаются только к кэш-памяти, то время доступа стремится к с. С другой стороны, если h—»0 и каждый раз нужно обращаться к основной памяти, то время доступа стремится к с+ш: сначала требуется время с для проверки кэш-памяти (в данном случае безуспешной), а затем время m для обращения к основной памяти. В некоторых системах обращение к основной памятиможет начинаться параллельно с исследованием кэш-памяти, чтобы в случае неудачного поиска цикл обращения к основной памяти уже начался. Однако эта стратегия требует способности останавливать процесс обращения к основной памяти в случае результативного обращения к кэш-памяти, что делает разработку такого компьютера более сложной. Основная память и кэш-память делятся на блоки фиксированного размера с учетом принципа локальности. Блоки внутри кэш-памяти обычно называют строками кэш-памяти (cache lines). Если обращение к кэш-памяти нерезультативно, из основной памяти в кэш-память загружается вся строка, а не только необходимое слово. Например, если строка состоит из 64 байтов, обращение к адресу 260 повлечет за собой загрузку в кэш-память всей строки, то есть с 256-го по 319-й байт.

Возможно, через некоторое время понадобятся другие слова из этой строки. Такой путь обращения к памяти более эффективен, чем вызов каждого слова по отдельности, потому что вызвать к слов 1 раз можно гораздо быстрее, чем 1 слово к раз. Если входные сообщения кэш-памяти содержат более одного слова, это значит, что будет меньше таких входных сообщений и, следовательно, меньше непроизводительных затрат.

Разработка кэш-памяти очень важна для процессоров с высокой производительностью.

Первый вопрос - размер кэш-памяти. Чем больше размер, тем лучше работает память, но тем дороже она стоит.

Второй вопрос — размер строки кэш-памяти. Кэш-память объемом 16 Кбайт можно разделить на 1К строк по 16 байтов, 2К строк по 8 байтов и т. д. Третий вопрос - как устроена кэш-память, то есть, как она определяет, какие именно слова содержатся в ней в данный момент. Устройство кэш-памяти мы рассмотрим подробно в главе 4.

Четвертый вопрос — должны ли команды и данные находиться вместе в общей кэш-памяти. Проще разработать смежную кэш-память, в которой хранятся и данные, и команды. При этом вызов команд и данных автоматически уравновешивается. Тем не менее, в настоящее время существует тенденция к использованию разделенной кэш-памяти, когда команды хранятся в одной кэш-памяти, а данные - в другой. Такая структура также называется Гарвардской (Harvard Architecture), поскольку идея использования отдельной памяти для команд и отдельной памяти для данных впервые воплотилась в компьютере Маге III, который был создай Говардом Айкеном в Гарварде. Современные разработчики пошли по этому пути, поскольку сейчас широко используются процессоры с конвейерами, а при такой организации должна быть возможность одновременного доступа и к командам, и к данным (операндам). Разделенная кэш-память позволяет осуществлять параллельный доступ, а общая — нет. К тому же, поскольку команды обычно не меняются во время выполнения, содержание командной кэш-памяти никогда не приходится записывать обратно в основную память.

Наконец, пятый вопрос - количество блоков кэш-памяти. В настоящее время очень часто кэш-память первого уровня располагается прямо на микросхеме процессора, кэш-память второго уровня - не на самой микросхеме, но в корпусе процессора, а кэш-память третьего уровня - еще дальше от процессора.

Модульное ОЗУ.

Сборка модулей памяти и их типы

Со времен появления полупроводниковой памяти и до начала 90-х годов все микросхемы памяти производились, продавались и устанавливались на плату компьютера по отдельности. Эти микросхемы вмещали от 1 Кбит до 1 Мбит информации и выше. В первых персональных компьютерах часто оставлялись пустые разъемы, чтобы покупатель в случае необходимости мог вставить дополнительные микросхемы.

В настоящее время распространен другой подход. Группа микросхем (обычно 8 или 16) монтируется на одну крошечную печатную плату и продается как один блок. Он называется SIMM (Single Inline Memory Module - модуль памяти, имеющий выводы с одной стороны) или DIMM (Dual Inline Memory Module - модуль памяти, у которого выводы расположены с двух сторон). У первого из них контакты расположены только на одной стороне печатной платы (выводы на второй стороне дублируют первую), а у второго - на обеих сторонах. Схема SIMM изображена на рис. 2.14.

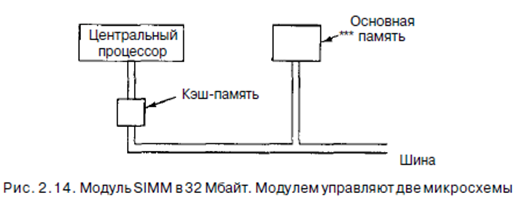
Обычный модуль SIMM содержит 8 микросхем по 32 Мбит (4 Мбайт) каждая. Таким образом, весь модуль вмещает 32 Мбайт информации. Во многие компьютеры встраивается 4 модуля, следовательно, при использовании модулей SIMM по 32 Мбайт общий объем памяти составляет 128 Мбайт. При необходимости данные модули SIMM можно заменить модулями с большей вместимостью (64 Мбайт и выше).

У первых модулей SIMM было 30 контактов, и они могли передавать 8 битов

информации за один раз. Остальные контакты использовались для адресации и контроля. Более поздние модули содержали уже 72 контакта и передавали 32 бита информации за один раз. Для компьютера Pentium, который требовал одновременной передачи 64 битов, эти модули соединялись по два, и каждый из них доставлял половину требуемых битов. В настоящее время стандартным способом сборки является модуль DIMM. У него на каждой стороне платы находится по 84 позолоченных контакта, то есть всего 168. DIMM способен передавать 64 бита данных за раз. Вместимость DIMM обычно составляет 64 Мбайт и выше. В электронных записных книжках обычно используется модуль DIMM меньшего размера, который называется SO-DIMM (Small Outline DIMM). Модули SIMM и DIMM могут содержать бит четности или код исправления ошибок, однако, поскольку вероятность

возникновения ошибок в модуле 1 ошибка в 10 лет, в большинстве обычных компьютеров методы обнаружения и исправления ошибок не применяются.

Лекция 5. Информационное обеспечение компьютера.

1. Шины информационного обмена.

2. Символьные терминалы.

3. Символьное кодирование информации.

<2 3 456 7 8 >

Дата добавления: 2016-10-26; просмотров: 16505;