Расчет сложных трехфазных цепей
Сложная трехфазная цепь, например, объединенная энергосистема, может содержать большое число трехфазных генераторов, линий электропередачи, приемников трехфазной энергии. Схема такой цепи представляет собой типичный пример сложной цепи переменного тока. Установившейся режим в такой схеме может быть описан системой алгебраических уравнений с комплексными коэффициентами, составленных по одному из методов расчета сложных цепей (метод законов Кирхгофа, метод контурных токов, метод узловых потенциалов). Наиболее рациональным методом расчета таких трехфазных цепей является метод узловых потенциалов, при этом составление уравнений и их решение производится в матричной форме.
В более простых случаях возможно применение любых методов расчета, позволяющих получить экономичное решение задачи. На рис. 96 представлена схема параллельного подключения нескольких трехфазных приемников с различными схемами соединения фаз к одному генератору. В представленной схеме расчет фазных и линейных токов каждого из приемников может выполняться индивидуально и независимо друг от друга, а линейные токи источника определяются как геометрические суммы токов всех приемников, например,  .
.

Как известно, объединенная трехфазная энергосистема работает в режиме, близком к симметричному. В симметричном режиме токи и напряжения смежных фаз отличаются только углом сдвига на ±120º. Расчет токов и напряжений в установившемся симметричном режиме производится только для одной из фаз, например для фазы А, при этом трехфазные цепи представляются однофазными эквивалентными схемами. На рис. 97 представлена символьная схема передачи энергии от трехфазного генератора к удаленным приемникам, а на рис. 98 – расчетная однофазная схема для той же цепи. На расчетной схеме рис. 98 каждому звену электропередачи соответствует его стандартная схема замещения.


В результате расчетов определяются токи и напряжения во всех элементах схемы для фазы А, например 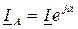 . Аналогичные токи и напряжения в фазе В определяется умножением соответствующих величин фазы А на поворотный множитель
. Аналогичные токи и напряжения в фазе В определяется умножением соответствующих величин фазы А на поворотный множитель 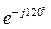 , а для фазы С – на множитель
, а для фазы С – на множитель 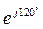 , например:
, например:
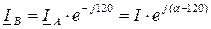 ,
,
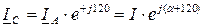 .
.
Дата добавления: 2016-10-18; просмотров: 1915;











