Совместное действие изгиба и кручения

На практике кручение часто сопровождается изгибом. С таким сложным видом деформации приходится встречаться, например, при расчете валов машин и механизмов, когда силы, передающие валу, не проходят через его ось. Пусть на вал (рис. 9.5) насажено зубчатое колесо, передающее окружное усилие Р от другого зубчатого колеса на расстоянии R от центра вала. Перенесем силу Р в центр вала (т.О). Для этого приложим в т.О по прямой, параллельной силе Р, две равные силы Р, но направленные в противоположные стороны. Тогда для вала получим пару сил с моментом 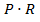(силы, составляющие эту пару, на рисунке перечеркнуты двумя черточками), скручивающих вал, и силу Р, приложенную в центре вала и вызывающую его изгиб.

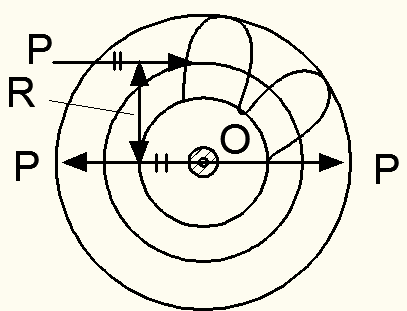
Рисунок 9.5 – Совместное действие изгиба и кручения на вал

Согласно принципу независимости действия сил напряжения в валу от изгиба и кручения рассчитывается отдельно. Тогда при изгибе в сечениях вала возникают нормальные напряжения 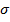и касательные напряжения 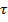, а при кручении – только касательные напряжения 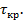Касательными напряжениями 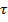при изгибе от перерезывающей силы в расчете валов обычно пренебрегают, так эти напряжения значительно меньше касательных напряжений от кручения .

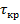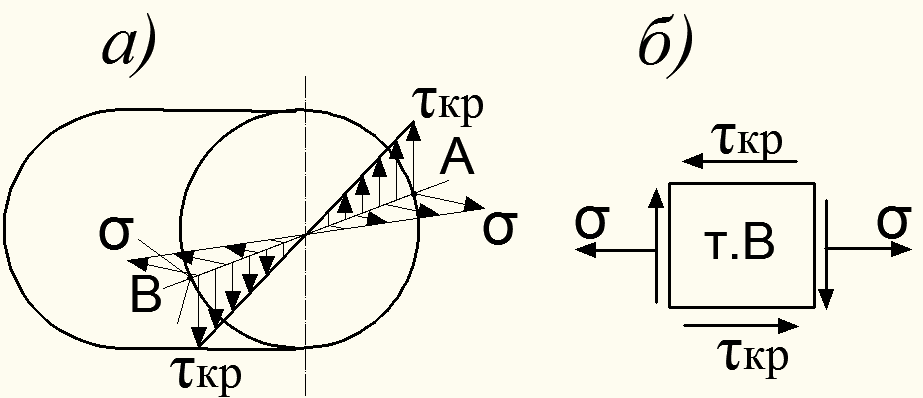
Рисунок 9.6 – Распределение напряжений в сечении вала

Напряжение 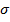от изгиба вала распределяются по линейному закону и достигают наибольших значений в точках А, В на поверхности вала (рис.9.6, а):

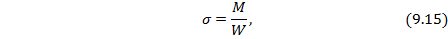
где 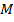– изгибающий момент в сечении вала; 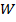– момент сопротивления сечения (для круглого вала = );

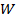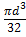Касательные напряжения от кручения вала 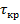также распределяются по линейному закону и достигают максимума на поверхности вала (см. рис. 9.6, а):

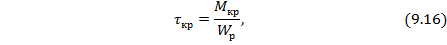
где 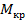– крутящий момент в сечении вала (для примера на рис. 9.5 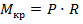); 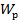– полярный момент сопротивления сечения (для круглого вала = ).

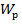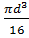Каждое из этих напряжений, взятое в отдельности, может быть меньше допускаемого напряжения для соответствующего вида деформации. Однако одновременное их действие и учет в опасной точке сечения может оказаться опасным для вала (рис. 9.6, б). В этих условиях для проверки прочности используют приведенные (эквивалентные) напряжения 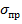. Например, по 3-й теории наибольших касательных напряжений условие прочности будет иметь вид:

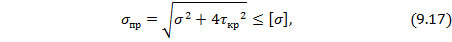
где 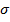и 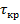– напряжения при изгибе и кручении, рассчитываемые по формуле (9.15) и (9.16); 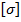– допускаемое напряжение при изгибе.