Совместное действие изгиба и растяжения (сжатия)
Вид деформации, когда на балку действует поперечная нагрузка и продольные силы растяжения или сжатия вдоль ее оси, называется продольно-поперечным или сложным изгибом. Так, для балки, показанной на рис. 9.3, поперечная нагрузка интенсивностью q вызывает поперечный изгиб, а растягивающая сила Р – растяжение (в случае действия сжимающей силы Р балка испытывает изгиб и сжатие). Тогда в поперечном сечении балки с координатой х будут иметь место два вида простейших деформаций, вызывающих нормальные напряжения (касательными напряжениями пренебрегают из-за их малой величины):
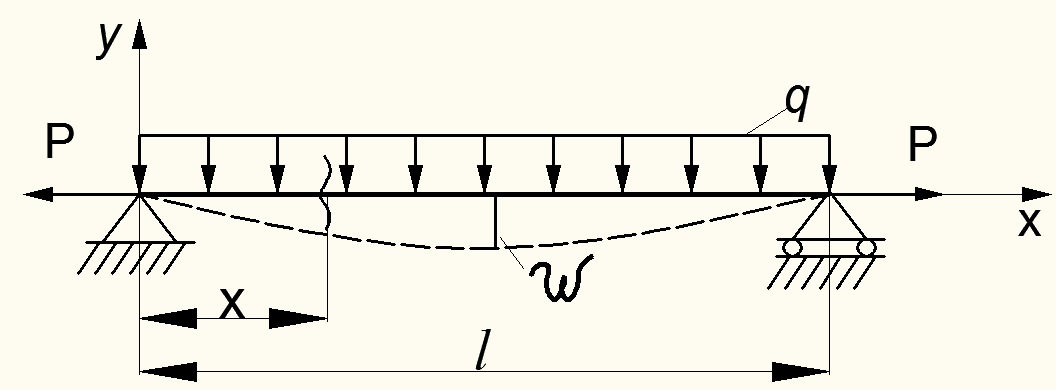
Рисунок 9.3 – Продольно-поперечный изгиб балки
1) изгиб, приводящий к нормальным напряжениям
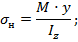
2) растяжение, при котором
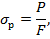
где 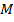 – изгибающий момент в поперечном сечении с координатой х; y – ордината по высоте сечения балки; F – площадь поперечного сечения балки.
– изгибающий момент в поперечном сечении с координатой х; y – ордината по высоте сечения балки; F – площадь поперечного сечения балки.
Тогда на основе принципа независимости действия сил полное напряжение в любой точке по высоте сечения равно:
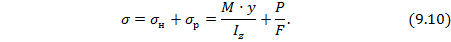
Покажем на рис. 9.4 распределение напряжений по высоте прямоугольного сечения при рассмотренном виде нагружения балки (см. рис. 9.4):
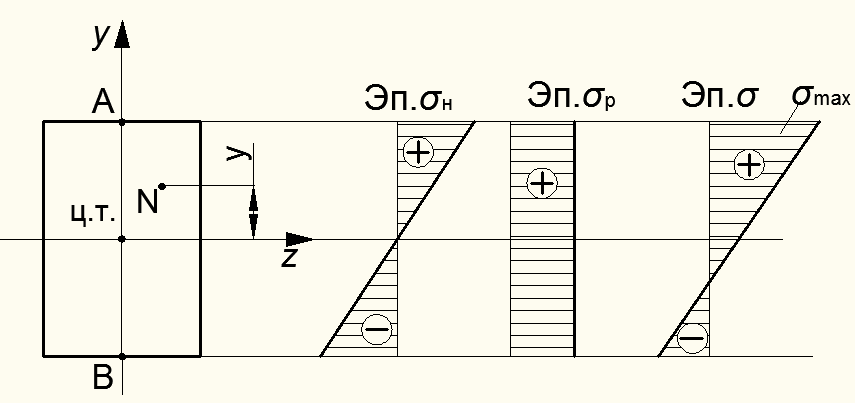
Рисунок 9.4 – Распределение нормальных напряжений при продольно-поперечном изгибе балки
Из рисунка видно, что наибольшие суммарные напряжения от изгиба и растяжения будут в наиболее удаленной т.А от центра тяжести сечения балки:
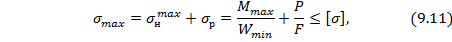
где 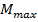 – максимальный изгибающий момент в опасном сечении балки;
– максимальный изгибающий момент в опасном сечении балки; 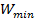 – минимальный момент сопротивления сечения балки, равный
– минимальный момент сопротивления сечения балки, равный 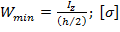 – допускаемые напряжения.
– допускаемые напряжения.
В этом случае предполагается, что балка настолько жестка и мало прогибается, что продольная сила Р все время действует параллельно оси балки без учета ее искривления.
При сжимающей продольной силе Р сжимающие нормальные напряжения балки будет 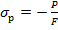 и наиболее нагруженной точкой по высоте сечения окажется т.В (см. рис. 9.4):
и наиболее нагруженной точкой по высоте сечения окажется т.В (см. рис. 9.4):
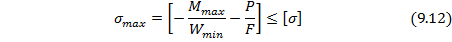
В общем случае растягивающей или сжимающей продольной силы Р условие прочности при продольно-поперечном изгибе балки имеет вид:
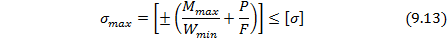
Прогибы балки при продольно-поперечном изгибе можно получить, интегрируя дифференциальное уравнение упругой линии балки:
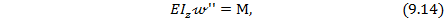
где М – изгибающий момент от поперечной к продольной нагрузки балки 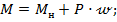 здесь первое слагаемое соответствует изгибающему моменту от поперечной нагрузки, а второе – изгибающему моменту от продольной силы.
здесь первое слагаемое соответствует изгибающему моменту от поперечной нагрузки, а второе – изгибающему моменту от продольной силы.
Для коротких и жестких балок ( 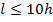 ) максимальный суммарный прогиб от изгиба и продольного нагружения 𝓌 можно приблизительно считать равным изгибу от поперечной нагрузки
) максимальный суммарный прогиб от изгиба и продольного нагружения 𝓌 можно приблизительно считать равным изгибу от поперечной нагрузки 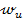 , который рассчитывается любым аналитическим или энергетическим методами.
, который рассчитывается любым аналитическим или энергетическим методами.
Дата добавления: 2016-10-18; просмотров: 6015;











