Расчет переходного процесса

При расчете переходного процесса скорости при приложении к якорной цепи напряжения, равного половине номинального ( 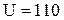В) пренебрежем электромагнитными переходными процессами в двигателе (т.к. длительность электромагнитных переходных процессов намного меньше длительности разгона привода и переходный процесс разгона приближенно можно оценить без их учета). Для расчета переходного процесса воспользуемся уравнением механической характеристики двигателя постоянного тока

,

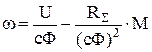где U – напряжение на якоре двигателя, с – конструктивная постоянная двигателя, Ф – магнитный поток двигателя, 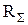- сопротивление обмоток якоря и добавочных полюсов.

Кроме того, для расчета понадобится основное уравнение движения электропривода:

.

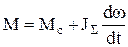Если выразить момент двигателя из основного уравнения движения и подставить его в уравнение механической характеристики, то получим дифференциальное уравнение:

,

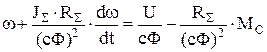которое можно представить в виде:

,

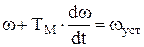где:

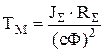- механическая постоянная времени,

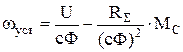- установившаяся скорость вращения.

Решением такого дифференциального уравнения при нулевых начальных условиях ( 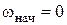), является выражение вида:

.

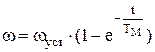Определим все переменные, необходимые для решения дифференциального уравнения:

,

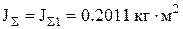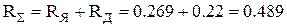Ом,

,

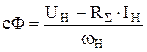где:

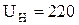В – номинальное напряжение двигателя,

рад/с – номинальная скорость вращения,

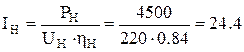А – номинальный ток двигателя,

следовательно:

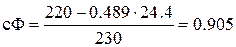Вс.

При напряжении на якоре, равном половине номинального и моменте нагрузки 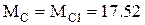Нм, установившаяся скорость вращения:

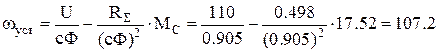рад/с.

Постоянная времени:

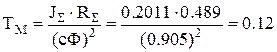с.

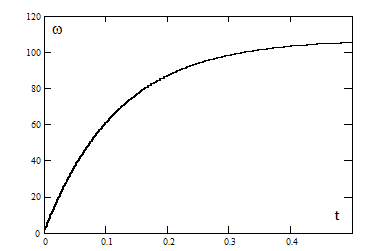
Переходный процесс скорости описывается уравнением:

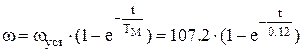
Длительность переходного процесса (время пуска) составляет:

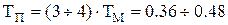с.

Для расчета переходного процесса тока воспользуемся уравнением электрического равновесия якорной цепи двигателя постоянного тока:

,

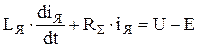где Е – ЭДС якорной цепи:

.

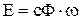Таким образом ЭДС якорной цепи зависит от скорости вращения двигателя и изменяется в процессе пуска. С учетом этого уравнение электрического равновесия можно записать в виде:

,

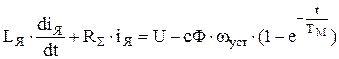Или ,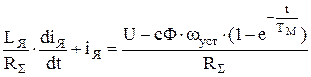

Где - электрическая постоянная времени якорной цепи,

Решение подобного дифференциального уравнения можно записать в виде:

,

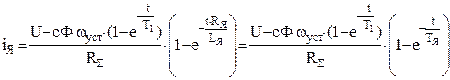подставляя численные значения в это выражение получим:

.

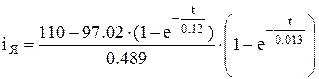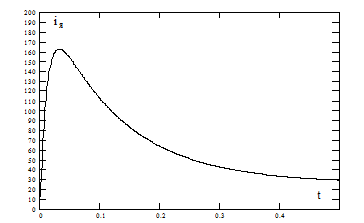
Из выражения видно, что механическая постоянная времени электропривода 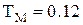c, на порядок больше электрической постоянной времени якорной цепи 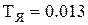с, то есть длительность электромагнитных переходных процессов намного меньше длительности разгона привода. Установившееся значение тока при равно:

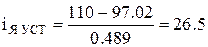А.

График переходного процесса тока показан на рис. 3.4.

4. Контрольные вопросы к защите

1. Классификация электроприводов.

2. Основное уравнение движения электропривода.

3. Приведение моментов, сил и моментов инерции к одной оси вращения.

4. Нагрузочные диаграммы электропривода.

5. Нагрев электродвигателей.

6. Номинальные режимы работы электродвигателей.

7. Выбор мощности электродвигателя.

8. Выбор типа электродвигателя.

9. Переходные процессы в электроприводе.

Список литературы

1. Фотиев М.М. Электрооборудование прокатных и трубных цехов. М.: Металлургия., 1995. – 256 с.

2. Касаткин В.С., Немцов М.В. Электротехника. М.: Высш. шк., 2000. – 542с.

3. Ключев В.И. Теория электропривода: Учебник для вузов. – М.: Энергоатомиздат, 1985. – 560 с.