Как найти предел знакочередующейся последовательности?
Такая последовательность уже неоднократно встречалась в статье, например, первая скрипка теоретического параграфа 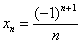 .
.
Действительно, как аналитически найти предел знакочередующейся последовательности, если знак то «плюс», то «минус»?
И я, наконец-то, заряжаю в свой револьвер тот самый волшебный патрон:
Пример 13
Найти предел последовательности 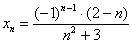
Решение: на первом шаге следует найти предел последовательности 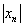 , которая составлена из модулей членов. Знак модуля уничтожает возможный минус, поэтому чтобы получить
, которая составлена из модулей членов. Знак модуля уничтожает возможный минус, поэтому чтобы получить 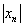 , нужно попросту убрать множитель, обеспечивающий знакочередование. Чаще всего это «мигалка»:
, нужно попросту убрать множитель, обеспечивающий знакочередование. Чаще всего это «мигалка»:
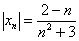
Теперь как ни в чём не бывало, вымучиваем наш обычный предел:
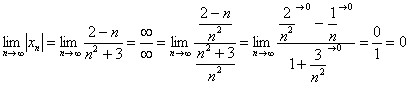
Получено конечное число. Очевидно, что знакочередование не поменяет сути – члены последовательности будут «прыгать» вокруг своего предела, бесконечно близко приближаясь к нему. Собственно, это проиллюстрировано на единственном рисунке данного урока.
Ситуация принципиально такая же, как, например, у более простых последовательностей 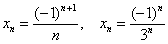 .
.
Ответ: так как последовательность является знакочередующейся и 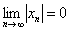 , то
, то 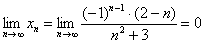 .
.
Если в ходе исследования знакочередующейся последовательности 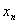 получен бесконечный результат
получен бесконечный результат 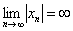 (или если предела нет), то у последовательности
(или если предела нет), то у последовательности 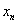 предела не существует вообще. Такой инцидент напоминает историю с
предела не существует вообще. Такой инцидент напоминает историю с 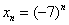 .
.
Наше увлекательное путешествие в мир последовательностей подошло к концу и, надеюсь, оно составило достойную конкуренцию Вконтакте =) =) =)
Успехов в учёбе!
Решения и ответы:
Пример 2: Решение:
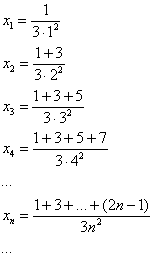
Найдём предел последовательности:
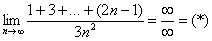
Используем формулу суммы 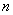 первых членов арифметической прогрессии
первых членов арифметической прогрессии 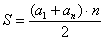 .
.
В данном случае 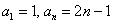
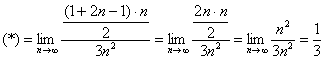
Пример 4: Решение:
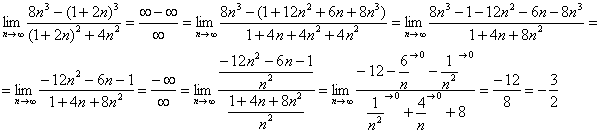
Пример 6: Решение:
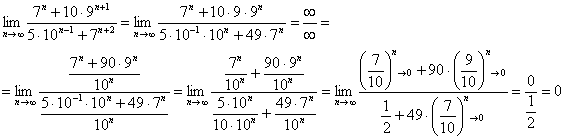
Пример 8: Решение:
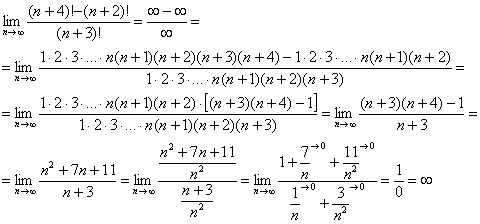
Пример 10: Решение: последовательность 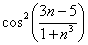 – ограничена:
– ограничена: 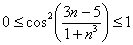 , а последовательность
, а последовательность 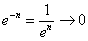 , значит, по соответствующей теореме:
, значит, по соответствующей теореме:
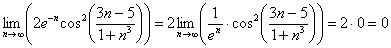
Пример 12: Решение:
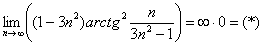
Заменим бесконечно малую эквивалентной: 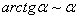 при
при 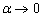 .
.
В данном примере 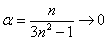 .
.
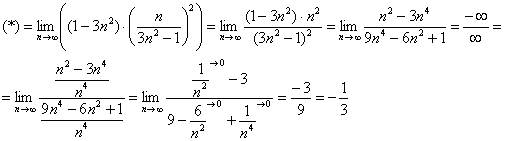
Дата добавления: 2021-01-26; просмотров: 508;











