Понятие числовой последовательности

Числовая последовательность. Как найти предел последовательности?

Рассматриваемая тема относится как к курсу математического анализа, так и к основам дискретной математики.

Понятие числовой последовательности

Сначала задумаемся над самим словом: а что такое последовательность? Последовательность – это когда что-то расположено за чем-то. Например, последовательность действий, последовательность времён года. Или когда кто-то расположен за кем-то. Например, последовательность людей в очереди, последовательность слонов на тропе к водопою.

Немедленно проясним характерные признаки последовательности. Во-первых, члены последовательности располагаются строго в определённом порядке. Так, если двух человек в очереди поменять местами, то это уже будет другая последовательность. Во-вторых, каждому члену последовательности можно присвоить порядковый номер:

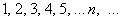
С числами всё аналогично. Пусть каждому натуральному значению 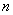по некоторому правилупоставлено в соответствие действительное число 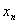. Тогда говорят, что задана числовая последовательность .

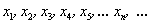Да, в математических задачах в отличие от жизненных ситуаций последовательность почти всегда содержит бесконечно много чисел.

При этом:
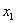называют первым членом последовательности;
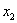– вторым членом последовательности;
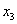– третьим членом последовательности;
…
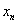– энным или общим членом последовательности;

…На практике последовательность обычно задаётся

формулой общего члена, например: 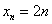– последовательность положительных чётных чисел:

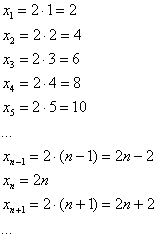
Таким образом, запись 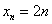однозначно определяет все члены последовательности – это и есть то правило (формула), по которому натуральным значениям 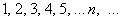в соответствие ставятся числа 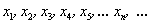. Поэтому последовательность часто коротко обозначают общим членом, причём вместо «икс» могут использоваться другие латинские буквы, например:

Последовательность положительных нечётных чисел :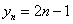

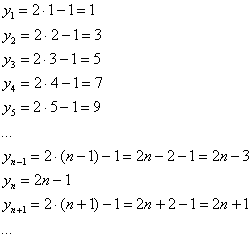
Ещё одна распространённая последовательность :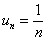

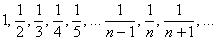
Как, наверное, многие подметили, переменная «эн» играет роль своеобразного счётчика.

На самом деле с числовыми последовательностями мы имели дело ещё в средних классах школы. Вспомним арифметическую прогрессию. Определение переписывать не буду, коснёмся самой сути на конкретном примере. Пусть 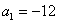– первый член, а 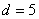– шаг арифметической прогрессии. Тогда:
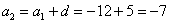– второй член данной прогрессии;
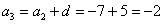– третий член данной прогрессии;
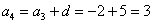– четвертый;
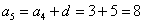– пятый;
…
И, очевидно, энный член задаётся рекуррентной формулой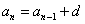

Примечание: в рекуррентной формуле каждый следующий член выражается через предыдущий член или даже через целое множество предыдущих членов.

Полученная формула малопригодна на практике – чтобы добраться, скажем, до 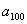, нужно перебрать все предыдущие члены. И в математике выведено более удобное выражение энного члена арифметической прогрессии: 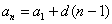. В нашем случае:

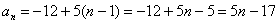
Подставьте в формулу 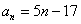натуральные номера 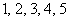и проверьте правильность построенной выше числовой последовательности.

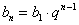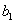Аналогичные выкладки можно провести для геометрической прогрессии, энный член которой задаётся формулой , где – первый член 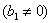, а 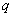– знаменатель прогрессии 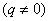. В заданиях по матану первый член частенько равен единице.

Примеры:

прогрессия 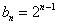задаёт последовательность ;
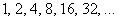прогрессия 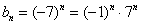задаёт последовательность ;
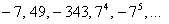прогрессия 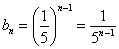задаёт последовательность ;
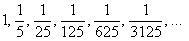прогрессия 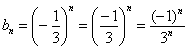задаёт последовательность .

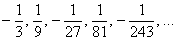Надеюсь, все знают, что –1 в нечётной степени равно –1, а в чётной – единице.

Прогрессию называют бесконечно убывающей, если 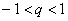(последние два случая).

Давайте добавим в свой список двух новых друзей, один из которых только что постучался в матрицу монитора:

Последовательность 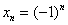на математическом жаргоне называют «мигалкой»:

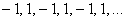
Таким образом, члены последовательности могут повторяться. Так, в рассмотренном примере последовательность состоит из двух бесконечно чередующихся чисел.

А бывает ли так, что последовательность состоит из одинаковых чисел? Конечно. Например, 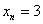задаёт бесконечное количество «троек». Для эстетов есть случай, когда в формуле всё же формально фигурирует «эн»: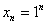

Факториал: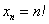
Всего лишь свёрнутая запись произведения:

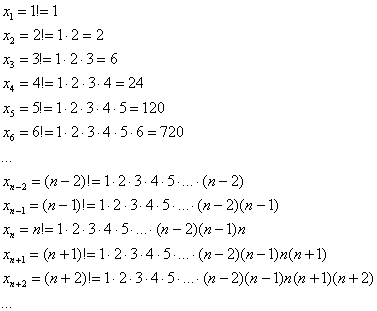
Отнюдь не графомания, пригодится для задач ;-) Рекомендую осмыслить-запомнить и даже переписать в тетрадь. …Пришёл тут в голову один вопрос: а почему никто не создаёт такие полезные граффити? Едет себе человек в поезде, смотрит в окно и изучает факториалы. Панки отдыхают =)

Возможно, некоторым читателям всё-таки ещё не до конца понятно, как расписать члены последовательности, зная общий член. Тот редкий случай, когда контрольный выстрел возвращает к жизни:

Разберёмся с последовательностью .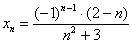

Сначала подставим в энный член значение 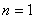и внимательно проведём вычисления:

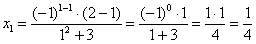
Далее подставим в общий член :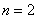

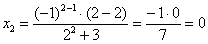
Потом подставим следующий номер :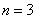

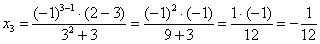
Четвёрку:

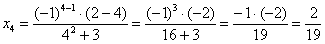
Чего уж, теперь и отличную отметку не зазорно заработать:

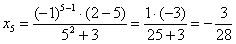
и так далее… пока разогреется самый последний чайник!