САР по отклонению напряжения на двигателе.

Принципиальная схема системы управления одним двигателем приведена на рис. 7.3а, а структурная схема линейной модели – на рис. 7.3б.

Сумматором (рис. 7.3а) формируется сигнал управления

,

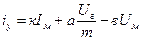где к, а, в – коэффициенты пропорциональности; т – количество последовательно включённых ТЭД.

Уравнения для приращений моментов и ЭДС двигателя Е_м имеют вид

ΔМ – ΔМ_С=JрΔω (7.1)

ΔЕ_м=с_ек_ф(i₀Δω + ω₀Δi_в0), (7.2)

где ΔМ=с_мк_фI₀Δi_в – приращение момента двигателя; с_м – постоянная двигателя по моменту; к_ф – коэффициент пропорциональности между магнитным потоком двигателя и током возбуждения; I₀ – начальное значение тока якоря двигателя; Δi_в – приращение тока возбуждения; ΔМ_С – приращение момента сопротивления; J – приведённый к двигателю момент инерции привода; р – оператор дифференцирования; Δω – приращение угловой скорости вращения якоря двигателя; с_е – постоянная двигателя по ЭДС; i_в0 и ω₀ – начальные значения тока возбуждения и угловой скорости соответственно.

Поскольку принято считать, что САР работают практически точно, а после возникновения возмущающего воздействия ΔМ_С ток в цепи якоря остаётся неизменным, то приращение напряжения на двигателе ΔU_м равно приращению его ЭДС ΔЕ_м.

Передаточные функции звеньев структурной схемы, приведённой на рис. 7.3б имеют вид:

усилитель У ,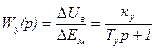

где к_у – коэффициент усиления усилителя У по напряжению; ΔU_в – приращение напряжения возбуждения; Т_у – постоянная времени усилителя;

обмотка возбуждения L1 двигателя ,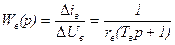

где r_в и Т_в – сопротивление и постоянная времени обмотки возбуждения;

якорь двигателя .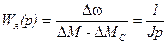

В соответствии со структурной схемой

ΔЕ_м(р)=с_ек_фi_в0(ΔМ- ΔМ_С)W_я(р) – с_ек_фω₀ΔЕ_мW_у(р)W_в(р)

Поскольку ΔМ=-с_мк_фI₀ΔЕ_мW_у(р), то после преобразования получаем

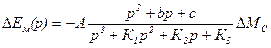,(7.3)

где 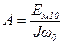; Е_м10- начальное значение ЭДС двигателя; 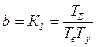; Т_Σ=Т_в+Т_у; 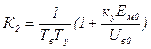; ; 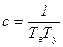; 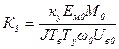U_в0=r_вi₀ .

В квазистационарном режиме (р=0) выражение (7.1) принимает вид

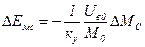. (7.4)

Из приведённых выражений видно, что динамическая ΔЕ_м (р) и статическая ΔЕ_мс ошибки САР имеют положительые значения при отрицательных приращениях ΔМ_С, т.е. при снижениях нагрузки.

Анализ САР в общем виде при свободном и вынужденном движении возможен с помощью решения уравнения (7.3) и построения зависимости ΔЕ_м(t) от возмущающего воздействия ΔМ_С. Практический интерес представляют затухающие переходные процессы, характер которых определяется корнями уравнения р³+К₁р²+К₂р+К₃=0.