Сприйняття яскравості, пороговий контраст


 

Рівень світлового відчуття (світлота) безпосередньо пов'язаний з освітленістю сітківки або зі світловим потоком, що отримується одиницею її площі. Остання величина визначається яскравістю випромінювання. Знаючи зв'язок світлоти з яскравістю, можна перейти від психологічних величин, вимір яких складний. Знаючи цей зв'язок та значення світлоти, можна розраховувати значення яскравостей.

Вебер, досліджуючи відчуття сили тяжіння, знайшов, що мінімальне відчуття залежить не від приросту стимул-реакції (причини, що викликає відчуття), а від співвідношення цього приросту до первинного значення стимул-реакції. Яскравість, що мінімально виявляється, залежить не від різниці порогу DВ, а від його cпіввідношення до первоначально узятої яскравості. Інакше, різниця порогу DВ пов'язаний з вихідною яскравістю В. Це можна надати у вигляді равенства

 

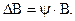(2.5)

 

Коефіцієнт y є сталою, тому різниця порогу DВ лінійно залежить від яскравості В. Тому диференціальний поріг (пороговий контраст) розраховують наступним чином

 

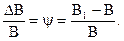(2.6)

 

Якщо диференціальний поріг є сталою, то деякий приріст світлоти можна виразити числом порогів.

Фехнер припустив, що мінімальний приріст стимул-реакції (яскравості) і відчуття (світлоти), що викликається нею, є нескінченно малими величинами. Враховуючи це отримують

 

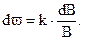(2.7)

 

Інтегруючи цей вираз, отримуємо загальне співвідношення між світловою стимул-реакцією – яскравістю та рівнем викликаного ним відчуття світлотою – закон Вебера–Фехнера

 

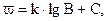(2.8)

 

де w – світлота, що виражається числом порогів;

k і С – коефіцієнти лінійного рівняння.

 

Для розрахунку приросту світлоти за приростом яскравості необхідно встановити числове значення коефіцієнта k. З рівняння (2.8) це співвідношення Dw:DlgВ.

Нехай Dw дорівнює одному порогу. Тоді DlgВ є приріст логарифма яскравості. Якщо Dw= 1, то 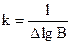. З рівняння (2.8):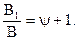

Логарифмуючи цей вираз, отримують 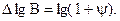Отже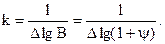

Багато дослідників вважають, що в межах виконання закону Вебера–Фехнера при великих кутових розмірах об'єкту спостереження пороговий контраст в межах Dy=0,05–0,1. Тоді Dk=25–30. За формулою (2.8) можна розрахувати, що світлота, наприклад, при переході від яскравості В=10 кд×м–2 до яскравості В1=100 кд×м–2 зростає на 25–50 порогів.

Таким чином, сприйняття яскравостей описується законом Вебера–Фехнера, за яким рівень зорового відчуття, що виражається світлотою, пропорційний логарифму яскравості. Критерієм закону Вебера–Фехнера є постійність диференціального порогу. Дослідження, що почалися ще в минулому столітті, показали, що закон Вебера–Фехнера дотримується в деякому інтервалі яскравостей з точністю, достатньою для багатьох випадків практики. Лаурі вивчав постійність порогу на фотометричному полі, розташованому на тлі постійної яскравості. Така методика дозволила встановити закономерності сприйняття при адаптації ока на певну яскравість. Розглядалися два рівні адаптації – 34,3 і 318 кд×м–2. Криві Лаурі наведені на рис. 2.8.

 

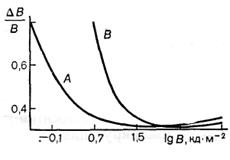
Рис. 2.8. Криві Лаурі: А – адаптація на 34,3 кд×м–2; В – на 318 кд×м–2

 

З графіків видно, що диференціальний поріг в області малих яркостей швидко падає із зміною Ст В області середніх яркостей він змінюється трохи, і його можна вважати постійним. У цьому інтервалі закон Вебера–Фехнера виконується. Область виконання закону залежить від рівня адаптації ока; при малих рівнях яскравості ця область починається раніше, ніж при великих. Мінімальне значення DВ:В належить до яскравості адаптації.

Міз надав дані Лаурі у вигляді функції контрастної чутливості ока k=f(lgВ). Результатом інтегрування вказаної функції є крива сприйняття – залежність числа порогів розрізнення від логарифмів яскравості (залежність за законом Вебера–Фехнера), однак на підставі експериментальних даних.

Контрастною чутливістюока (k) називається його здатність до розрізнення яскравостей суміжних ділянок. Вона зворотна диференціальному порогу. Чим менший контраст виявляє око, тим більша його контрастна чутливість. Чим більше число порогів Dw виявляє око в даному інтервалі яскравостей DВ, тим вища його контрастна чутливість. Отже:

 

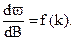(2.9)

 

Інтегруючи цей вираз, отримаємо співвідношення між світлотою і яскравістю залежно від контрастної чутливості ока:

 

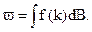(2.10)

 

Криві контрастної чутливості ока А і спийняття В, отримані Мізом за даними Лаурі, наведені на рис. 2.9.

Крапками зазначено рівень адаптації, при якому були виміри. З рис. 2.9 видно, що максимум кривої контрастної чутливості спостерігається при яскравості адаптації.

Крива сприйняття, розрахована на підставі кривих Лаурі, прямолінійна лише на деякій ділянці, де виконується закон Вебера–Фехнера. Яскравість адаптації знаходиться в середині цієї ділянки.

На практиці часто світлоту визначають за усередненими формулами при деяких умовах освітлення, що простіше, ніж розрахунок з врахуванням яскравості адаптації.

 

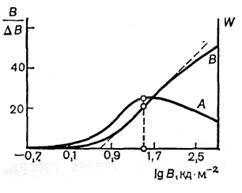
Рис. 2.9. Криві Міза

 

 


Дата добавления: 2021-01-11; просмотров: 398;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.009 сек.