Характеристики ступени компрессора
В теории компрессоров часто используют безразмерные характеристики, представляющие собой зависимость коэффициента адиабатического напора 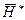 и КПД ступени от коэффициента расхода
и КПД ступени от коэффициента расхода 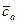 при постоянных значениях uк.пр . Легко убедиться в том, что параметры
при постоянных значениях uк.пр . Легко убедиться в том, что параметры 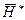 и
и 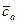 являются критериальными. В частности, коэффициент расхода может быть представлен как
являются критериальными. В частности, коэффициент расхода может быть представлен как 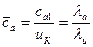 , т.е. является функцией критериальных параметров и однозначно определяет значение угла β1 и угла атаки на лопатках рабочего колеса.
, т.е. является функцией критериальных параметров и однозначно определяет значение угла β1 и угла атаки на лопатках рабочего колеса.
При постоянном значении β1 и β2 , как следует из треугольников скоростей, закрутка рабочего тела в колесе должна быть примерно пропорциональна u .
Следовательно, адиабатическая работа должна изменяться пропорционально квадрату окружной скорости, т.е. коэффициент 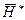 должен быть приблизительно постоянным. Таким образом. Безразмерные характеристики ступеней гораздо меньше зависят от окружной скорости колеса, чем характеристики, представленные в обычных координатах.
должен быть приблизительно постоянным. Таким образом. Безразмерные характеристики ступеней гораздо меньше зависят от окружной скорости колеса, чем характеристики, представленные в обычных координатах.
Слабая зависимость безразмерных характеристик от uк.пр облегчает анализ их протекания.
Рассмотри изменение 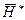 и ηст* по
и ηст* по 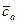 . При постоянном значении окружной скорости (uк=const) вместо изменения
. При постоянном значении окружной скорости (uк=const) вместо изменения 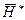 можно рассматривать изменение
можно рассматривать изменение 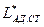 ,а изменение
,а изменение 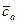 можно заменить изменением осевой скорости с1а .
можно заменить изменением осевой скорости с1а .
На рис. 18 показаны треугольники скоростей для рабочего колеса осевой ступени при трёх различных значениях осевой скорости.
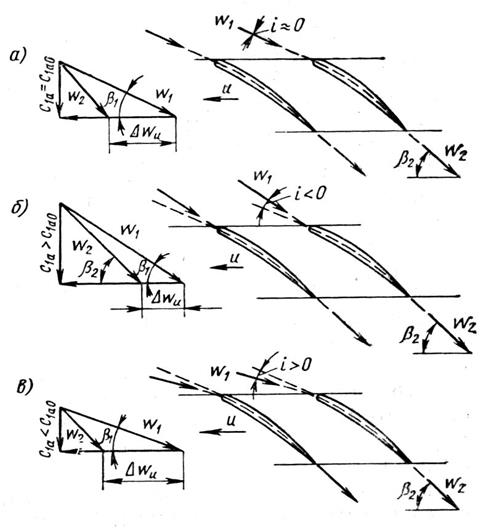
Рис. 18
Как видно, изменение осевой скорости непосредственно сказывается на величине угла атаки i на лопатках рабочего колеса и на величине закрутки потока в колесе Δwu .
Увеличение с1а приводит к увеличению β1 , т.е. к уменьшению угла атаки.
Направление вектора скорости w2 за колесом изменяется мало, т.е. β2≈const. В результате при увеличении с1а закрутка потока в колесе Δwu уменьшиться.
Уменьшение осевой скорости, наоборот, приведёт к увеличению угла атаки и к увеличению закрутки потока в рабочем колесе.
Аналогичный результат получается и при 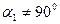 .
.
Указанное изменение закрутки при изменении осевой скорости определяет характер изменения работы вращения ступени по коэффициенту расхода.
Пренебрегая изменением Lu по радиусу работу на валу ступени при постоянном значении окружной скорости согласно
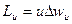
следует считать пропорциональной значению Δwu на среднем радиусе. Из треугольника скоростей (см. рис. 19) получим (при с1а=с1а и α1=900):
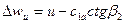 . (24)
. (24)
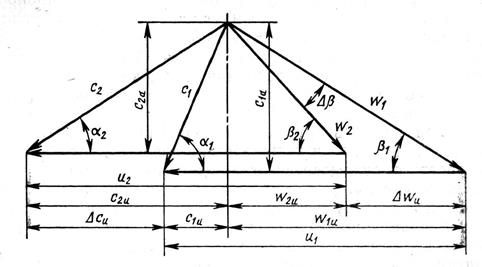
Рис. 19
Таким образом, если принять значение угла β2 постоянным, то зависимость Δwu и соответственно Lст от с1а должна быть линейной.
Причём при типичных для осевых ступеней значениях β2<900 работа вращения ступени уменьшиться с ростом с1а (т.е. с ростом коэффициента расхода), как показано линией а – ана рис. 20.
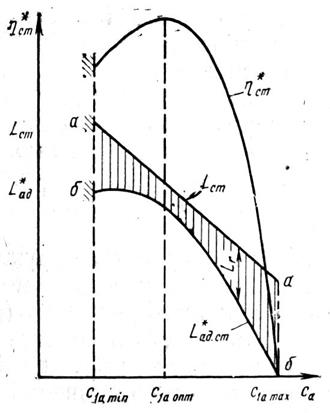
Рис. 20
Для анализа характера изменения 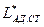 и ηст* при изменении с1а необходимо рассмотреть уравнение Бернулли для ступени
и ηст* при изменении с1а необходимо рассмотреть уравнение Бернулли для ступени
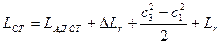 .
.
Пренебрегая величиной ΔLr и учитывая, что 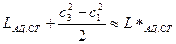 , получим
, получим
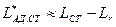 . (25)
. (25)
Согласно выражению КПД рабочего колеса
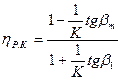
гидравлические потери в решётке профилей рабочего колеса равны
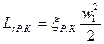 , (26)
, (26)
где коэффициент ξр.к при малых числах М для решётки с данными геометрическими параметрами зависит только от угла атаки. Типичная зависимость ξ=f(i) показана на рис. 21
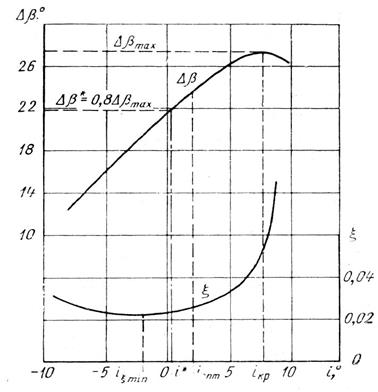
Рис. 21
На рис. 22 эта зависимость перестроена по коэффициенту расхода 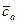 с учётом того, что увеличение
с учётом того, что увеличение 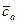 соответствует уменьшению i .
соответствует уменьшению i .
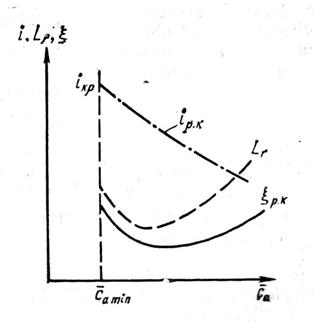
Рис. 22
Значение 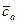 min соответствует критическому углу атаки, за которым находится область срывных режимов обтекания рабочих лопаток.
min соответствует критическому углу атаки, за которым находится область срывных режимов обтекания рабочих лопаток.
На рис. 22 также показано изменение Lr для рабочего колеса, которое аналогично изменению ξ .Некоторое различие между кривыми объясняется влиянием изменения w1 при изменении 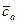 .
.
Аналогичным образом изменяются и потери в спрямляющем аппарате. Поэтому кривая Lr на рис. 22 изображает характер изменения потерь при изменении 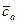 не только в рабочем колесе, но и в ступени в целом, и, вычтя соответствующие ей отрезки из ординат линии а – а на рис. 20, получим в соответствии с формулой (25) кривую изменения адиабатической работы ступени
не только в рабочем колесе, но и в ступени в целом, и, вычтя соответствующие ей отрезки из ординат линии а – а на рис. 20, получим в соответствии с формулой (25) кривую изменения адиабатической работы ступени 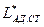 по с1а (кривая б – б) .
по с1а (кривая б – б) .
Соотношение 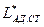 и LСТ согласно формуле адиабатического КПД ступени
и LСТ согласно формуле адиабатического КПД ступени 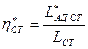 можно определить значение КПД ступени при каждом значении с1а.
можно определить значение КПД ступени при каждом значении с1а.
Проанализируем полученные кривые. Так как Lст уменьшается с ростом с1а, максимум η*ст достигается при значении с1а опт , лежащим несколько левее минимума потерь, а максимум напора, т.е. максимума 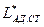 располагается ещё левее.
располагается ещё левее.
Полезный (рабочий) диапазон изменения с1а, ограничен здесь слева границей срыва с1а min , а справа – значением с1а max . при котором из-за падения Lст и одновременного возрастания гидравлических потерь адиабатический напор, а вместе с ним и КПД ступени обращаются в нуль.
Отметим, что в рассматриваемом случае пониженных окружных скоростей ступень при осевых скоростях, близких к с1а max , может работать на нескольких принципиально различных режимах (рис. 23).
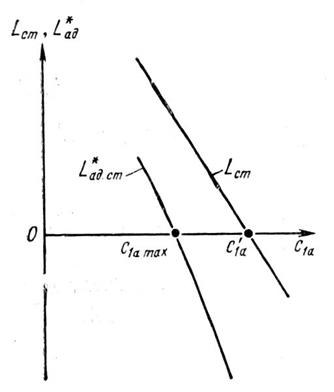
Рис. 23
При с1а< с1а max ступень потребляет мощность и создаёт напор. Эта область обычных компрессорных режимов её работы.
При увеличении коэффициента расхода до значения, соответствующих с1а> с’1a , не только 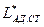 , но и Lст становятся отрицательными.
, но и Lст становятся отрицательными.
Другими словами, ступень не потребляет, а создаёт мощность на валу колеса за счёт работы расширения потока (р3*<р1*).
Эта область называется областью турбинных режимов работы ступени.
При с1а= с’1a ступень не потребляет и не создаёт мощности, а свободно вращается под действием проходящего через неё потока рабочего тела (режим авторотации).
Наконец, между с1а max и с’1a лежит область режимов, в которой компрессорная ступень потребляет мощность, но не создаёт напора (η*ст<0), работая как мешалка.
Рассмотрим влияние типа ступени на её характеристику.
Как видно из формулы (24), чем больше β2 , тем в меньшей степени изменяется Lст при изменении с1а . С другой стороны, используя формулы (24) и
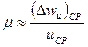
и опуская для упрощения индекс «ср», получим для коэффициента нагрузки осевой ступени (при осевом входе) выражение
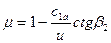 . (27)
. (27)
, откуда следует, что чем меньше 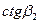 , тем выше коэффициент нагрузки. Сравнивая эти два положения, нетрудно прийти к заключению, что чем выше коэффициент нагрузки, тем более полого протекает зависимость Lст от с1а.
, тем выше коэффициент нагрузки. Сравнивая эти два положения, нетрудно прийти к заключению, что чем выше коэффициент нагрузки, тем более полого протекает зависимость Lст от с1а.
Это утверждение будет справедливым как для осевых ступеней с 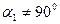 , так и для центробежных и диагональных ступеней.
, так и для центробежных и диагональных ступеней.
Рассмотрим, например , центробежную ступень с радиальными лопатками рабочего колеса. У такой ступени угол β2 близок к 900 и соответственно коэффициент нагрузки близок к единице.
В то же время при β2≈900 изменение расходной составляющей скорости потока за колесом с2r практически не влияет на с2u . Следовательно, при осевом входе согласно формуле
Эффективная работа такой ступени не будет зависеть от расхода рабочего тела и характеристика ступени будет иметь вид, показанный на рис. 24, а.
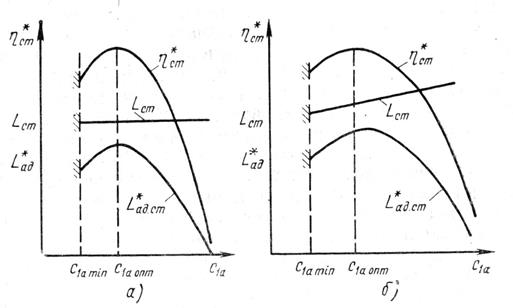
Рис. 24. Характеристика центробежного компрессора:
а – β2≈900 ; б – β2>900
В этом случае максимумы Lст и η*ст совпадают и, кроме того, режим нулевого напора ca max достигается позднее, чем для осевых ступеней с обычными значениями коэффициента нагрузки μ<0,3…0,4.
В этом случае говорят, что центробежная ступень имеет более пологую характеристику, чем осевая.
В центробежной ступени с лопатками, загнутыми по направлению вращения (β2≈900), увеличение расхода приведёт к увеличению с2u , т.е. к увеличению Lст . Характеристика имеет вид, показанный на рис. 24, б.
Лекция № 5
Дата добавления: 2021-01-11; просмотров: 485;











