Основные параметры многоступенчатого компрессора и связь их с параметрами ступеней

На рис. 1 приведена схема. Многоступенчатого осевого компрессора с указанием обозначений характерных сечений проточной части.

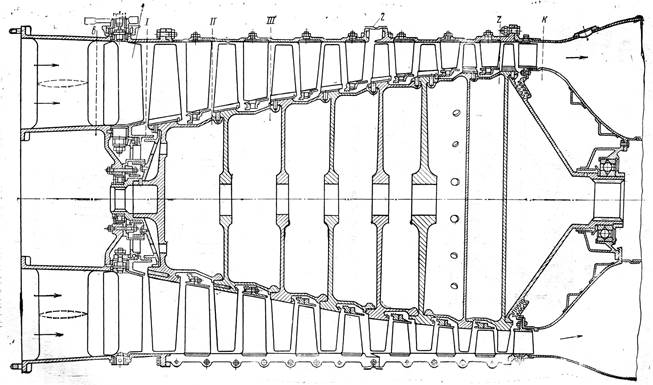
Рис. 1. Многоступенчатый осевой компрессор:

1 – ВНА с поворотными лопатками; 2 – лента перепуска воздуха

Здесь в – сечение на входе в компрессор;

к – сечение на выходе из компрессора;

1, 11, 111, …z – сечение на входе в первую, вторую, третью и т.д. ступени.

Сечение в располагается перед входным направляющим аппаратом (ВНА) или перед рабочим колесом первой ступени, если ВНА отсутствует; в последнем случае сечение в совпадает с сечением 1 .

Все параметры, относящиеся к произвольно взятой ступени компрессора, снабжаются индексом «i».

Исло ступеней обозначаются индексом z .

На рис. 2 приведена схема осецентробежного компрессора, а на рис. 3 - схема двухступенчатого центробежного компрессора также с указанием характерных сечений преточной части.

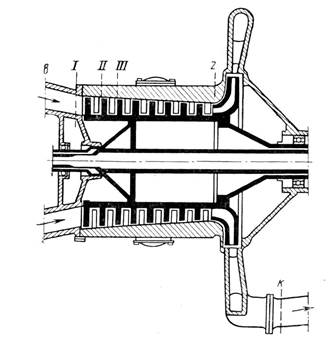
Рис 2. Осецентробежный компрессор

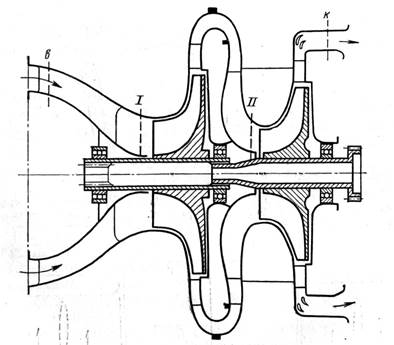
Рис. 3

При расчёте многоступенчатого компрессора используются следующие параметры:

а) степень повышения давления

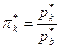; (1)

б) работа вращения вала компрессора L_к и адиабатическая работа ;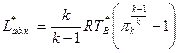

в)расход рабочего тела через компрессор G_В;

г) частота вращения ротора n и мощность, затрачиваемая на вращение, N_k=G_в.L_k;

д) Удельная производительность

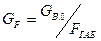, (2)

где G_В.0 – расход рабочего телапри максимальной частоте вращения и стандартных условий на входе;

F_габ – габаритная площадь проточной части компрессора;

е) адиабатический КПД по аналогии с КПД ступени

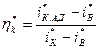, (3)

где i^*_к.ад - полное теплосодержание потока за компрессором при адиабатическом сжатии,

или (без учёта влияния переменности теплоёмкости рабочего тела)

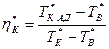, (4)

где - температура заторможенного потока за компрессором при адиабатическом сжатии.

Умножая числитель и знаменатель правой части формулы (4)на 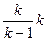, получим

. (5)

Таким образом, КПД компрессора равен отношению адиабатической работы сжатия в компрессоре к работе на его вращение.

Иногда КПД компрессора определяют по термодинамическим (статическим) значениям температуры и давления

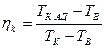. (6)

Некоторые особенности характеристики компрессора связаны со средним значением коэффициента нагрузки его ступеней

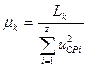. (7)

Рассмотрим взаимосвязь между основными параметрами компрессора и параметрами входящих в него ступеней.

Так работа вращения ротора многоступенчатого компрессора равна сумме работ вращения колёс всех ступеней:

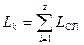. (8)

С другой стороны, степень повышения давления в компрессоре равна произведению степеней повышения давления отдельных его ступеней:

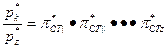… . (9)

Удельная производительность многоступенчатого осевого компрессора определяется параметрами его первой ступени. Расход рабочего тела через сечение в равен

,

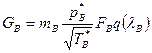где р_В и q(λ_B) - среднемассовые значения полного напора и плотности тока в этом сечении

Причём стандартными условиями на входе в компрессор принято считать р_В^*=101300 Па и Т_В^*=288 К.

С другой стороны, для осевого компрессора

и ,

где 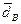- относительный диаметр втулки первой ступени.

Тогда удельная производительность осевого компрессора согласно (2) равна

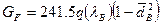. (10)

Следовательно, максимальная удельная производительность компрессора не может превышать 240 кг/с на каждый квадратный метр габаритной площади входа.

В современных компрессорах диаметр втулки в первой ступени доходит до 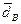=0.3…0.45.

Расход рабочего тела в компрессоре возрастает пропорционально осевой составляющей скорости с_1а. В дозвуковых осевых компрессорах при с_1а.=170 – 195 м/с, удельная производительность может доходить до 150 кг/(м²с).

В сверхзвуковых компрессорах при с_1а =210 – 240 м/с, соответственно удельная производительность может достигать 170 – 190 кг/(м₂с).

Поскольку при этом плотность тока на входе в колесо уже превышает 90% от максимально возможного значения, дальнейшее увеличение с_1а.даже в сверхзвуковых ступенях нецелесообразно.

Наиболее сложной является связь между КПД компрессора и его ступеней. На рис. 4 изображён процесс сжатия рабочего тела в трёхступенчатом компрессоре в pv-координатах.

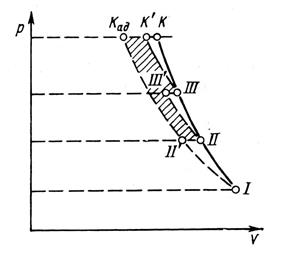
Рис. 4

Точки 1, 11,111 изображают состояние рабочего тела на входе в первую, вторую и третью ступени.

Линия 1 – К_ад изображает процесс адиабатического сжатия рабочего тела во всём компрессоре.

В то же время процессы адиабатического сжатия для второй и третей ступеней при тех значениях давления и плотности потока, которые в действительности имеют место на входе в эти ступени, изобразятся линиями 11 – 111^’ и 111 – К^’ . Как видно из рисунка, сумма адиабатических работ сжатия рабочего тела во всех трёх ступенях оказывается больше адиабатической работы компрессора на величину, пропорциональную заштрихованной площади.

Этот результат представляет собой эффект теплового сопротивления в многоступенчатом компрессоре и связан с тем, что температура рабочего тела на входе в каждую последующую ступень оказывается выше, чем она была бы при отсутствия потерь. А это приводит к увеличению потребной работы сжатия рабочего тела в каждой последующей ступени.

Связь между КПД компрессора и КПД входящих в него ступеней можно установить, если известны значения адиабатическое работы сжатия в каждой ступени. Используя КПД компрессора (5), равенство (8) можно переписать в виде

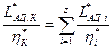, (11)

где η_i^* - КПД i-й ступени, откуда

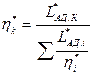. (12)

В случае равенства КПД всех ступеней из формулы (12) следует

. (13)

При некоторых допущениях связь между адиабатическим КПД компрессора и КПД его ступеней может быть установлена в более удобном для анализа и расчётов виде.

Предположим, что компрессор состоит из бесконечно большого числа ступеней с бесконечно малым повышением давления в каждом из них.

Выделим в таком компрессоре сечениями x и y произвольную ступень (рис.5).

Рис. 5

Обозначим давление и температуру рабочего тела в сечении x через p и T , а в сечении y соответственно через p+dp и T+dT

Если бы процесс сжатия рабочего тела в этой ступени был адиабатическим, то повышение температуры в ней было бы равно

.

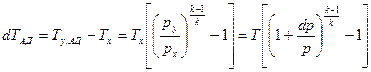Разложив выражение в ряд по степеням dp/p и ограничиваясь в соответствии с принятым допущением только двумя первыми членами этого разложения, получим

.

Тогда адиабатический КПД ступени будет равен

.

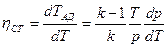Из полученного выражения следует, что изменения температуры и давления рабочего тела в ступени связаны уравнением

.

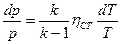Если принять далее, что КПД всех ступеней одинаков

,

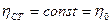то это уравнение после интегрирования даёт следующую связь между давлением и температурой в любом сечении компрессора:

.

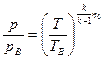Сравнивая полученные выражения с уравнением политропы

,

Приходим к выводу о том, что в рассматриваемых условиях процесс сжатия рабочего тела в компрессоре является политропическим процессом с постоянным показателем политропы, связанным с КПД ступени равенством

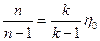(14)

Запишем выражение (6) в виде

.

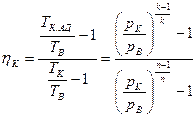Заменяя p_k /p_B на π_к , окончательно получим

. (15)

Зависимость η_к от π_к и η₀ ,определяемая по формуле (15), приведена на рис. 6.

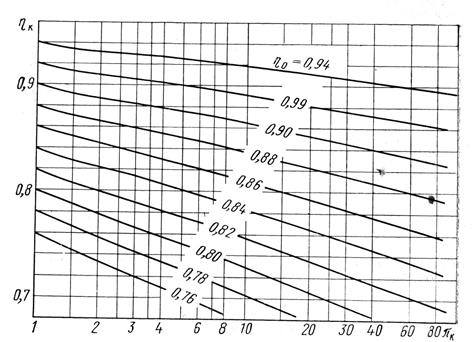
Рис. 6

Как видно из этих данных, снижение КПД компрессора по сравнению с КПД ступени оказывается тем более существенным, чем выше π_к и тем ниже КПД ступени.

Лекция № 2