ОПРЕДЕЛЕНИЕ ЭНЕРГЕТИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПОСТОЯННОГО ТОКА

Электрическим током называется направленное движение электрически заряженных частиц. В веществе носителями тока являются свободные заряды, а ток, создаваемый ими, называется током проводимости. При этом под свободными зарядами понимают заряженные микрочастицы, не связанные с конкретными атомами или молекулами вещества и способные перемещаться в нем на расстояния, многократно превышающие размеры атомов и молекул. Вещества, содержащие свободные заряды, называют проводниками электрического тока. Если свободными зарядами являются электроны, что имеет место в случае металлов и их сплавов, то такие вещества называют проводниками первого рода. В электролитах (растворах солей, кислот и щелочей) свободными зарядами являются положительные и отрицательные ионы. Такие вещества называют проводниками второго рода. В проводниках первого рода перенос зарядов не сопровождается химическими превращениями, а в проводниках второго рода перенос зарядов ведет к химическим изменениям.

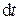Одной из основных характеристик тока является сила тока – скалярная величина, равная отношению заряда , проходящего через поперечное сечение проводника за бесконечно малый промежуток времени , к величине этого промежутка:

. (1)

В СИ сила тока измеряется в амперах. За положительное направление тока условно принимается направление упорядоченного дви­жения положительных зарядов. Если сила тока и его направление с течением време­ни не изменяется, то такой ток называется постоянным. Очевидно, что в этом случае сила тока численно равна заряду, проходящему через поперечное сечение проводника в единицу времени. В рамках данной работы рассматриваются постоянные токи, текущие в неподвижных проводниках. Для того чтобы вызвать такой ток, необхо­димо создать внутри проводника постоянное электрическое поле, что приводит к возникновению разности потенциалов на его концах .

Приборы, способные поддерживать постоянную разность потенциалов в проводниках, называются источниками постоянного тока. Ряд соединенных между собой проводников и источников тока образует электрическую цепь. Для поддержания постоянного тока необходимо обеспечить круговорот электрических зарядов. Следовательно, электрическая цепь постоянного тока должна быть замкнутой.

Условия существования постоянного электрического тока:

1) наличие свободных зарядов;

2) наличие электрического поля, действующего на эти заряды и вызывающего их направленное движение;

3) электрическая цепь должна быть замкнутой.

В источниках постоянного тока за счет химических реакций, фотоэлектрического эффекта и т.д. осуществляется пространственное разделение зарядов так, что на одном полюсе источника накапливается положительный заряд, а на другом – отрицательный. Возникающее при этом электрическое поле внутри источника противодействует разделению зарядов. Следовательно, разделение осуществляется силами, имеющими неэлектростатическую природу. Эти силы называют сторонними.

Если электрическую цепь разомкнуть, то при накоплении на полюсах источника определенного заряда (и достижении вследствие этого между ними соответствующей разности потенциалов) разделение зарядов прекращается. Прекращается при этом и работа сторонних сил. После замыкания цепи в проводниках её внешней части будет создано электрическое поле, которое, воздействуя на свободные заряды проводников, вызовет ток. Избыточные заряды отрицательного полюса источника начнут стекать во внешний участок цепи, а на положительном полюсе будет происходить нейтрализация его положительного заряда. В результате на обоих полюсах источника тока избыточный заряд уменьшится. Это приведет к тому, что в источнике снова начнется разделение зарядов, которое будет продолжаться все время, пока цепь остается замкнутой.

Во внешнем участке цепи совершается работа по переносу за­рядов силами электрического поля. Внутри же источника на грани­цах металлический электрод – электролит действуют сторонние си­лы, а внутри электролита – силы электрического поля. При этом сум­­марная работа сил электрического поля равна работе сторонних сил.

Характеристикой источника тока является скалярная величина, равная работе, совершаемой сторонними силами по переносу единичного положительного заряда, и называемая электродвижущей силой (ЭДС):

. (2)

В СИ ЭДС, как и электрический потенциал, измеряется в вольтах.

На рис.1 дан пример разветвленной замкнутой цепи постоянного тока, включающей два источника тока 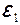, и резисторы 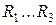. В качестве резисторов могут выступать нити ламп накаливания, спирали электронагревательных приборов, внутренние сопротивления источников тока и др.

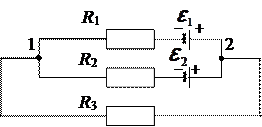Рис. 1. Разветвленная электрическая цепь

Разветвленная электрическая цепь содержит узлы, т.е. места соединения не менее трех проводников (точки 1 и 2 на рис. 1). На рис. 2 показан выделенный из разветвленной цепи неоднородный участок, содержащий резистор и источник тока.

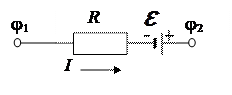Рис. 2. Неоднородный участок электрической цепи

В общем случае неоднородного участка цепи, содержащего источник тока, электрическое напряжение на концах участка вычисляется по формуле

, (3)

где 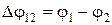– разность потенциалов на концах участка;

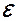– ЭДС источника тока.

Знак «+» перед ЭДС в формуле (3) выбирается в том случае, когда направление переноса положительных зарядов сторонними силами совпадает с направлением тока. Этот случай представлен на рис. 2.

Полное электрическое сопротивление неоднородного участка 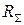складывается из сопротивления нагрузки 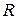(суммарное сопротивление всех резисторов и соединительных проводов) и внутреннего сопротивления источника тока :

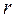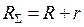. (4)

Зависимость между силой тока I, напряжением на концах участка цепи U и полным сопротивлением 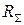этого участка определяется законом Ома (1826 г.):

. (5)

Для замкнутой цепи из формул (3)-(5), положив , нетрудно получить:

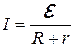. (6)

Если ток проходит по неподвижному проводнику и не сопровождается химическими реакциями (как в случае тока в металле), то вся работа по переносу зарядов , совершаемая электрическим полем, по закону сохранения энергии превращается в теплоту 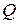, выделяющуюся в этом проводнике, т.е.

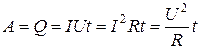. (7)

Выражение 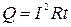представляет собой закон Джоуля–Ленца, экспериментально установленный независимо друг от друга Дж. Джоулем (1841 г.) и Э.Х. Ленцем (1842 г.). Согласно закону Джоуля-Ленца, количество теплоты, выделяемое в проводнике, пропорционально произведению квадрата силы тока, сопротивления и времени протекания тока.

Наряду с работой тока важной характеристикой электрической цепи является мощность тока. Мощность тока – это количество теплоты, выделяемой в проводнике в единицу времени. Она равна отношению теплоты, выделенной за время 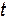, к этому интервалу времени, т.е.

. (8)

Следовательно, .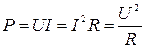

Исследуем физические характеристики замкнутой электрической цепи, включающей внешнее сопротивление 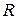, называемое полезной нагрузкой, и источник тока с электродвижущей силой 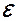и внутренним сопротивлением 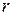(рис. 3).

При прохождении тока нагревается как внешнее, так и внутреннее сопротивление. Полная тепловая мощность 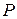, выделяемая в цепи постоянного тока, складывается из полезной мощности

, (9)

выделяемой во внешней цепи, и мощности тепловых потерь , выделяемой внутри источника тока, т.е.

. (10)

Рис. 3. Замкнутая электрическая цепь

Полная мощность развивается за счет сторонних сил, осуществляющих разделение зарядов в источнике тока.

Используя закон Ома для замкнутой цепи [см. формулу (6)], выражения для полезной и полной тепловых мощностей можно записать в виде

(11)

и

. (12)

Коэффициент полезного действия (КПД) электрической цепи определяется как отношение полезной мощности 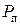к полной мощности :

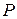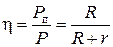. (13)

Таким образом, КПД зависит от соотношения внутреннего сопротивления и сопротивления нагрузки.

Каким должно быть сопротивление нагрузки 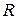для того, чтобы получить максимальную полезную мощность и максимальный КПД? Ответ на этот вопрос получим, исследовав графически и аналитически выражения (11) и (13).

Полная мощность 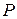и сила тока в цепи отличаются постоянным множителем [см. формулу (12)], поэтому их зависимости от сопротивления нагрузки R подобны (кривая 1 на рис. 4.). Эти величины максимальны при 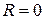, т.е. при коротком замыкании источника. Как видно из формул (11) и (13), при этом равны нулю 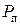и 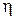(кривые 2 и 3).

При 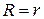полная мощность и сила тока равны половинам своих максимальных значений, КПД равен 0,5, а полезная мощность достигает своего максимального значения, равного половине полной мощности при этой нагрузке.

Чтобы убедиться, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока полезная мощность действительно максимальна, преобразуем правую часть выражения (11) следующим образом:

. (14)

Рис. 4. Зависимости силы тока и полной мощности (1),
полезной мощности (2) и КПД (3) от сопротивления нагрузки

Полезная мощность максимальна, когда знаменатель выражения (14) минимален. Возьмем производную по 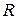от этого знаменателя и приравняем ее нулю. В результате получим уравнение

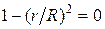, (15)

из которого следует, что условием максимума полезной мощности действительно является равенство внешнего и внутреннего сопротивлений.

Сам максимум полезной мощности определяется как

, (16)

то есть максимум полезной мощности равен четверти мощности короткого замыкания:

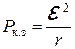. (17)

При неограниченном увеличении сопротивления нагрузки как полная мощность, так и полезная мощность стремятся к нулю (кривые 1 и 2), а КПД – к единице (кривая 3).

Из рис. 4 видно, что требования получения максимального тока в цепи, максимальной полезной мощности и максимального КПД противоречивы. Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника, но при этом близки к нулю полезная мощность и КПД, так как почти вся совершаемая источником тока работа идет на выделение теплоты на внутреннем сопротивлении r. Чтобы получить от данного источника тока максимальную полезную мощность, следует использовать согласованную нагрузку, т.е. нагрузку с сопротивлением .