КЛАССИФИКАЦИЯ ХИМИЧЕСКИХ РЕАКТОРОВ

Для реакторов характерны не только разнообразные конструктив­ные решения, но и различные способы их действия. Однако, несмот­ря на большие различия в конструкции, имеются общие практиче­ски для всех реакторов характеристики их функционирования. К ним относятся способ подвода реагентов и продуктов реакции; режим движения и перемешивания реагентов в реакционном про­странстве реактора; условия теплообмена и температурный режим в аппарате; фазовый состав реагентов и продуктов реакции. По­этому рассмотренная ранее классификация химических процессов по ряду признаков в известной степени относится и к реакторам, поскольку эти признаки существенно влияют на тип и конструкцию аппарата. Так, тепловой эффект реакции требует различных теп­лообменных устройств для отвода или подвода теплоты в реакци­онный объем. Поэтому деление процессов на экзо- и эндотермиче­ские требует выбора и соответствующего химического реактора. По тем же причинам реакторы, так же как и химические процессы, делят по наивысшей температуре процесса на низко- и высокотемпературные; по применяемому давлению — на аппараты, работающие на высоком, повышенном, нормальном и низком (под вакуумом) давлениях. Реакторы также классифицируют по фазо­вому состоянию реагентов на аппараты для осуществления гомоген­ных и различных гетерогенных процессов.

Но наиболее важными характеристиками работы любого хими­ческого реактора являются: 1) способ подвода и отвода реагентов; 2) режим движения и перемешивания реагентов; 3) температурный режим в реакционном объеме аппарата. Рассмотрим классифика­цию реакторов по этим признакам.

СПОСОБ ПОДВОДА И ОТВОДА РЕАГЕНТОВ

Он может осуществляться периодически, непрерывно и полупериодически (полунепрерывно). По аналогии с технологическими процессами различают и реакторы периодического, непрерывного и полунепрерывного действия.

Реакторы периодического действия. В такие реакторы реагенты загружают в начале операции. После определенного времени, не­обходимого для достижения заданной степени превращения, аппа­рат разгружают. Основные параметры процесса (концентрация реа­гентов и продуктов реакции, температура, давление и т. п.) изме­няются во времени. Среднюю скорость процесса можно измерить производительностью реактора. Истинная же скорость сильно и нелинейно меняется в течение периода работы ре­актора, во-первых, вследствие понижения концентрации исходных реагентов (по логарифмическому закону); во-вторых, вследствие неизотермичности процесса (обычно повышение температуры в на­чале периода и понижение в конце его). На скорость превращения часто сказывается также появление новых фаз в процессе работы такого реактора. Реакторы периодического действия работают, как правило, при сильном перемешивании реагентов, близком к полно­му смешению, и соответственно при одинаковой температуре во всем реакционном объеме в любой момент времени работы.

Реакторы непрерывного действия (проточные). Эти реакторы от пуска до остановки непрерывно (или систематическими порция­ми) питают исходными веществами и выводят из них продукты ре­акции. Величина, обратная времени пребывания (времени контак­та), называется объемной скоростью u, которую можно определить как отношение расхода материала (т. е. объем посту­пающего вещества V_p за время t) к полезному реакционному объ­ему V.

u= V_p/V.

Таким образом, объемная скорость может характеризовать производительность непрерывно действующего аппарата.

Сростом объемной скорости для процессов с одномаршрутными реакциями производительность (интенсивность) реактора увеличивается, однако при этом падает степень превращения (выход продукта) и растет сопротивление движению реагентов через аппарат.

рис. 4.

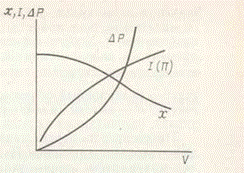
Поэтому объемную скорость целесообразно увеличивать лишь до некоторого предела, определяемого также экономическими соображениями.

Реакторы полунепрерывного действия. Реакторы этого типа хактеризуются тем, что сырье поступает в аппарат непрерывно или определенными порциями через равные промежутки времени, а продукты реакции выгружаются периодически. Возможна и непрерывная выгрузка продукта при периодической подаче сырья. Такие реакторы работают в переходном режиме, основные параметры процесса изменяются во времени.

РЕЖИМ ДВИЖЕНИЯ И ПЕРЕМЕШИВАНИЯ РЕАГЕНТОВ

Различают два вида перемешивания реагентов в потоке, проходящем через реактор — продольное (осевое) и радиальное. Продольное перемешивание обусловливает смешение компо­нентов потока только что вошедших в реактор с ранее находящими­ся в нем, т. е. перемешивание вдоль длины (высоты) реактора. Ра­диальное перемешивание обусловливает смешение ком­понентов внутри слоя движущегося потока по его радиусу. Продольное перемешивание выравнивает концентрационные и температурные поля по длине реактора, а радиальное — по его радиу­су. Именно продольное перемешивание определяет тип реактора, поскольку оно характеризует структуру потока, неоднородности поля скоростей, концентраций и температур, время пребывания компонентов в реакционной зоне, интенсивность смешения продук­тов реакции и исходных веществ, т. е. все, что так или иначе наиболее существенно влияет на протекание ХТП. Поэтому по режиму движения и перемешивания реагентов различают два предельных типа реакторов непрерывного действия: идеального вытеснения и полного (идеального) смешения (перемешивания).

Реактор идеального вытеснения. Эти реакторы характеризуются тем, что реагенты последовательно «слой» за «слоем» без перемешивания ламинарным потоком проходят весь реакционный путь, определяемый, как правило, длиной (высотой) аппарата.

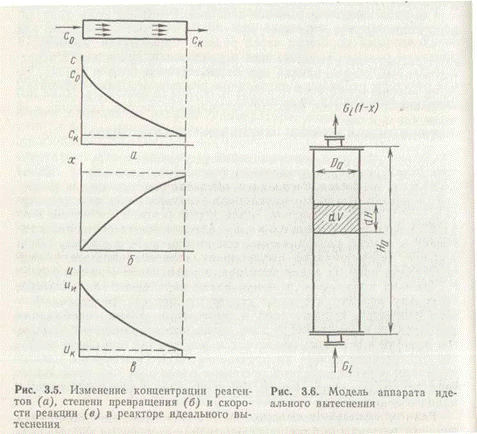
Реакторы полного смешения. Они характеризуются тем, что ча­стицы реагента (ион, молекула или зерно твердого материала), по­павшие в данный момент времени в аппарат, благодаря интенсив­ному перемешиванию имеют равную со всеми частицами вероятность первыми покинуть его. В реакторах полного смешения любой элемент объема мгновенно смешивается со всем содержимым реактора, так как скорость циркуляционных движений по высоте и сечению аппарата во много раз больше, чем скорость линейного перемещения по оси реактора. нецелесообраз­ным.

В системе Г—Т к типу смешения приближается режим работы аппаратов со взвешенным (кипящим) слоем (КС) зернистого ма­териала, причем наиболее близки к режиму полного смешения ап­параты КС с мешалками (рис. 7). Близки к режиму полного перемешивания аппараты циклонного типа, применяемые для сжигания серы и обжига сульфидных руд.

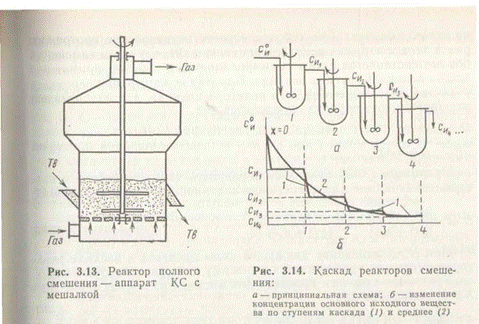
Каскад реакторов полного перемешивания. Их применяют для обеспечения достаточного общего выхода продукта, поскольку в единичном реакторе смешения при больших степенях превращения движущая сила процесса стремится к нулю и его скорость оказы­вается очень низкой. В каскаде реакторов полного перемешивания со сравнительно небольшой степенью превращения в каждой ступени (рис. 8) состав реакционной смеси изменяется при переходе из одного аппарата в другой, а в каждом реакторе концентрацион­ные и температурные поля безградиентны.

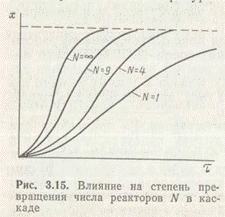Расчет каскада реакто­ров осуществляется путем суммирования всех изменений, происхо­дящих в каждой ступени каскада. С ростом числа реакторов в каскаде реакционный объем для до­стижения одной и той же степени превращения должен уменьшить­ся (рис. 9).

В каждом из рассмотренных типов реакторов реали­зуются различные температурные режимы работы.

По температурному режиму ре­акторы подразделяют на адиаба­тические, изотермические и поли­термические.

Адиабатические реакторы. Та­кие аппараты при спокойном (без перемешивания) течении потока реагентов не имеют теп­лообмена с окружающей средой, так как снабжены хорошей тепло­вой изоляцией. Вся теплота реакции аккумулируется потоком реагирующих веществ. Изотермические реакторы. Они имеют постоянную температуру во всех точках реакционного объема.

Способы достижения изотермичности различны. Можно прибли­зиться к изотермическим условиям процесса при помощи теплообменных устройств, помещенных в реакционный объем (для отвода теплоты в экзотермических и подвода в эндотермических реакциях). При этом в каждом элементарном объеме аппарата отвод или под­вод теплоты должен быть равен теплоте реакции. Изотермический режим достигается при интенсивном перемешивании реагентов в аппарате с мешалкой и в реакторах со взвешенным (кипящим, пенным) слоем, т. е. в аппаратах, в которых гидродинамический режим обеспечивает приближение к полному перемешиванию реагентов с продуктами реакции и инертными компонентами. В отдельных слу­чаях изотермичность в реакторе достигается за счет теплового рав­новесия экзо- и эндотермического превращений, например компен­сацией теплоты экзотермической реакции испарением растворителя (воды).

Политермические реакторы. Политермическими называются ре­акторы, в которых теплота реакции лишь частично компенсируется за счет отвода (подвода) теплоты или процессов с тепловым эффек­том, противоположным по знаку основному.

К политермическим аппаратам относят реакторы с малой степенью смешения реагирующих веществ и теплообменниками, помещенными внутри реакционного объема, например трубчатые контактные аппараты.

Для выбора типа реактора и опре­деления его производительности часто приходится прибегать к экс­периментальным исследованиям и переносу результатов экспери­мента на промышленные условия. Такой переход от лабораторных или опытно-промышленных условий реализации процесса к завод­ским осуществляется при помощи моделирования.

Моделирование.Моделирование — процесс сопоставления инфор­мации, полученной каким-либо образом, с информацией, которую получают на модели того или иного явления или процесса.

Моделями обычно называют системы, которые отражают отдельные, ограниченные в нужном направлении стороны явлений рассматриваемого процесса.

Моделирование процесса и соответствующего ему реактора, как правило, начинается с изучения физической сущности явления, ус­тановления переменных величин, влияющих на изучаемое явление, для чего составляют так называемую общую функциональную за­висимость. Эта зависимость может быть представлена в виде системы уравнений, связывающих входящие в нее основные параметры. Для описания того или иного технологического процесса, а следовательно, и аппарата, в котором этот процесс будет осуществляться, обыч­но используют следующие основные уравнения: 1) стехиометрические уравнения химической реакции; 2) уравнение скорости хими­ческой реакции; 3) уравнение сохранения массы вещества (мате­риальный баланс); 4) уравнение сохранения энергии (тепловой ба­ланс); 5) уравнение гидродинамики.

Как правило, система этих уравнений в аналитическом виде мо­жет быть решена лишь в очень редких случаях. Обычно же прихо­дится вводить целый ряд упрощающих допущений, начальных и граничных условий, после чего решение уравнений носит частный характер.

Различают три вида моделирования: по равенству основных частных соотношений, физическое и математическое.

Равенство основных частных соотношений.Данным видом моделирования иногда пользуются проектировщики, перенося не слиш­ком ответственные операции, уже осуществленные в промышлен­ности, с одних масштабов на другие.

Физическое моделирование.При физическом моделировании изу­чение данного явления происходит при его физическом воспроизве­дении в разных масштабах. При этом исследуется влияние на яв­ление различных факторов (чаще всего физических: скорости потоков, интенсивности перемешивания, температуры, давления, геометрических размеров и т. п.). Если изучается скорость какого-либо химико-технологического процесса, то предполагается, что кинетика собственно химического превращения известна, т. е. опи­сана соответствующим кинетическим уравнением.

Эксперименты проводятся непосредственно на самой изучаемой модели, а результаты исследования обобщаются в виде безразмер­ных критериальных уравнений. Безразмерная форма позволяет рас­пространить полученные зависимости на группу подобных между собой явлений. Как правило, критериальное уравнение включает в себя целый ряд критериев и симплексов подобия. Обычно разли­чают кинетические, диффузионные, тепловые и гидродинамические критерии подобия.

Кинетические критериивключают в основном три кри­терия:

критерий Дамкелера, характеризующий отношение скорости химической реакции к изменению концентрации основного исходного вещества по высоте (длине) реактора.
критерий Маргулиса, характеризует отношение скоро­сти процесса к скорости реакционного потока:

критерий Аррениуса- характеризует влияние температуры на процесс.

Диффузионные критерииописывают явления массопереноса в системе.

Диффузионный критерий Пекле, характеризующий
отношение скорости потока к приведенной скорости молекулярной
диффузии.
Диффузионный критерий Прандтля
характеризует отношение вязкостных свойств и диффузионной способности системы;

Критерий Нуссельта, характеризующий меру отношения скорости процесса к приведенной скорости молекулярной диффузии.

Гидродинамические критерииподобия: Рейнольдса, Архимеда, Фруда.

Тепловые критерииподобия:

Нуссельта, Прандтля.

Метод физического моделирования используют в инженерной практике для перехода от исследовательских разработок к промыш­ленному внедрению, особенно применительно к относительно не­сложным системам (например, гидравлическим или тепловым с од­нофазным потоком), поскольку приходится оперировать ограничен­ным числом критериев.

При анализе сложных, многофазных систем, с которыми чаще всего и приходится иметь дело в химико-технологических процессах, теория подобия наталкивается на принципиальные трудности, обус­ловленные сложностью масштабных переходов, большим набором определяющих критериев и симплексов подобия, многосторонно­стью связей в системе, неизбежностью введения упрощающих до­пущений и т. п.

Математическое моделирование. Математическое моделирование является методом, при котором изучение явления осуществляется на так называемой математической модели. Математической мо­делью принято называть систему уравнений (конечных или диффе­ренциальных), которая описывает всю совокупность явлений, со­ставляющих данный процесс. При этом предполагается, что физи­ческая сущность явления известна и для его описания найдена модель, адекватная (соответствующая) изучаемому физическому образцу. В модели должны быть учтены все основные факторы, влия­ющие на процесс. Для этого пользуются теоретическими предпо­сылками, характеризующими данное или сходное по природе яв­ление, а также результатами практической деятельности аналогич­ных или родственных производств и сведениями экспериментального характера.

Основная отличительная особенность математического модели­рования заключается в том, что все изменения условий (так назы­ваемая деформация модели) производятся на самой модели (систе­ма уравнений) путем параметрического изменения уравнений, до­бавления новых и перестройки уже внедренных связей. Поскольку все эти манипуляции выполняются кибернетически при помощи ЭВМ, надобность в экспери­менте или отпадает совсем, или резко сокращается число перемен­ных, подлежащих исследованию на физической модели.

При математическом моделировании можно решить и задачу оптимизации, т. е. установить такие параметры процесса, которые обеспечат максимальную производительность аппарата при задан­ном качестве готовой продукции. Именно благодаря широким воз­можностям метода математического моделирования, а также бур­ному развитию вычислительной техники этот метод находит все большее распространение не только при создании новых произ­водств, но и при совершенствовании действующих в виде создания автоматизированных систем управления технологическим процес­сом (АСУТП) и целой химико-технологической системой (ХТС).