Псевдо-периодические hiccups
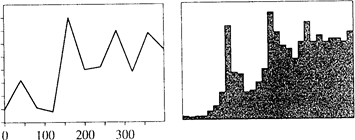
Вариограмма содержания золы, вычисленная для лага 40м для угля из Bowen Basin в Австралии, иллюстрирует проблему "псевдо-переодичные гикапы" (Рис. 4.8.a). Во-первых, два странных пика в h=150м и h=280м могут показаться признаком некоторой периодичности в угле, но это не соответствует физической природе угля. Хотя это и не заметно в начале, пробы лежат на почти регулярной сетке. Построение гистограммы расстояний между парами точек для каждого класса расстояний показывает, что это очевидный случай (Рис. 4.8.b). В этом случае решение будет достаточно простое. Все, что нам нужно, это лишь изменить длину лага. Вычисление вариограммы для лага 100м сглаживает эти особенности.
А б
100 200 300 400 500
Рис 4.8. (a) Эрратическая экспериментальная вариограмма для содержания золы в угле, (b) гистограмма, показывающая количество пар точек для каждого лага вариограммы. Заметьте пики гистограммы (160м и 320м)
Артефакты
Следующие два примера подтверждают точку зрения, что много проблем с вариограммами обуславливаются скорее "ошибкой оператора", чем статистическими проблемами в данных. Рисунок 4.9 показывает замечательную вариограмму "зубья пилы". Изучаемые переменные были высоко асимметричны, как содержание золота или урана. Существенному количеству данных, значения которые были ниже установленного предела точности, присваивалось значение нуль. Так как распределение данных похоже на логнормальное, то оказывается разумным использовать логарифмирование. Чтобы избежать проблемы с нулями, им было произвольно присвоено значение 0.00001 и поэтому после логарифмического преобразования появилась величина –0.5. Так как все другие логарифмы лежат в промежутки от -0.3 до +0.3, то –0.5 – экстремальные значения, и их местоположение полностью определяют форму вариограммы. В этом случае решение простое: установить нижнее значение борта 0.001 вместо 0.00001, в этом случае логарифм минимальной величины равен( – 0.3).
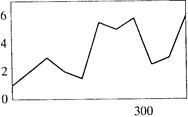
Рис 4.9. Эрратическая вариограмма "зубья пилы"
Вторая проблема - того же типа. В этом случае причиной проблемы было присутствие в исходных данных нулевых значений для мощности пласта. Они могут показать, что мощность в этом регионе уменьшается, но так как это неправдоподобно, то данные были перепроверены. Обнаружено, что нулевая мощность пласта получилась из-за отсутствия значений для кровли и подошвы пласта. Когда всем отсутствующим значениям присваивается –1, и когда студент в ходе исследования забывает провести тест на отсутствие данных перед вычислением мощности пласта, то вычитание –1 из –1 даст большое количество нулей, которые и будут определять форму вариограммы.
Эти ошибки скорее глупые. Читая это, каждый наверное уверен, что он не будет делать таких ошибок, но опыт показывает, что такого типа ошибки более распространенны, чем большинство из нас допускает. Поэтому единственный путь их устранения – это аккуратное исследование данных. Будет абсолютно бесполезно применять методы расчета "надежных" вариограмм для данных, имеющих ошибки и неточности. К счастью, компьютерные технологии теперь позволяют нам работать со связанными окнами. Поэтому возможно одновременно отображать несколько графиков (таких как базовая карта размещения данных, гистограмма и вариограмма), чтобы легче найти причину эрратического поведения.
Упражнения
Упр 4.1 Отсутствующие данные. На Рисунке 4.10 изображено 13 проб, расположенных через 5м. Значения содержаний имеются для 12 точек из 13, одна проба потеряна. Покажите, что для первого лага есть только 10 пар точек, и что значение g*(5)=4.7. Вычислите экспериментальную вариограмму для следующих двух лагов и нарисуйте ее. Иногда люди, ошибаясь, присваивают отсутствующему значению нуль. Вычислите первые три лага экспериментальной вариограммы и сравните с предыдущим.
Рис 4.10. Регулярные одномерные данные с одним отсутствующим значением
Упр. 4.2 Выбросы. На рисунке ниже изображено 13 проб, расположенных через 5м, с одним значением (90), значительно превосходящим остальные. Вычислите экспериментальную вариограмму для первых трех лагов и постройте ее. Посмотрите на проявление выброса, сравните эту вариограмму с одной из рассчитанных ранее (Рис 4.3.)
Рис 4.11. Регулярные одномерные данные, содержащие выброс
Упр. 4.3 Вариограммы в двухмерном измерении. В таблице ниже представлены 35 значений содержаний в пробах, расположенных по регулярной 100м на 100м сетке. Будет ли эта вариограмма изотропная?
Таблица 4.3. Тридцать пять значений содержаний в регулярной 100м на 100м сетке
| 3.6 | 2.8 | 4.1 | 4.6 | 5.3 | 3.8 | 4.2 |
| 3.6 | 3.5 | 5.2 | 4.5 | 6.1 | 4.4 | 4.0 |
| 5.1 | 3.8 | 4.9 | 3.3 | 5.7 | 6.2 | 6.3 |
| 4.2 | 4.0 | 5.6 | 4.2 | 4.9 | 5.3 | 4.4 |
Структурный анализ
Содержание
В этой главе представлено несколько случаев, показывающих, как проводить структурный анализ. Во-первых, рассматриваются принципиальные решения, которые должны быть сделаны геостатистиками. Стационарны ли данные? Изотропны ли данные? Должно ли изучение быть проведено в двухмерном или трехмерном измерении?
Первый пример – это относительно простое месторождение железной руды. Горизонтальная и вертикальная вариограммы были легко построены, что обеспечивает очень понятную иллюстрацию прямого вариограммного анализа. Второй пример касается архейского золоторудного месторождения, которое разрабатывается открытым способом. Поэтому здесь кроме редкой разведочной информации были доступны значения содержаний в близко расположенных взрывных скважинах. Третье представленное ниже месторождение – это осадочная золоторудная залежь с периодической вариограммой в одном направлении, потому что золото было отложено древним потоком вдоль русла. В противоположность предыдущим двум примерам, это месторождение имеет мощность только 1м и поэтому его изучение проводится в двухмерном пространстве, а не трехмерном.
Дата добавления: 2019-05-21; просмотров: 762;











