ВИВЧЕННЯ РОБОТИ РЕЛАКСАЦІЙНОГО ГЕНЕРАТОРА

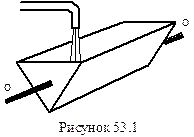Релаксаційні коливання - це коливання, які виникають в нелінійних системах і характерні тим, що складаються з процесів повільного та швидкого змін стану системи. В лінійних системах виконується лінійна залежність однієї величини від іншої . Наприклад, в механіці сила пружності пропорційна деформації F=−kx (закон Гука), а в електриці для металічного провідника сила струму пропорційна напрузі 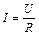(закон Ома). Якщо ж лінійні залежності порушуються, то маємо нелінійні системи.

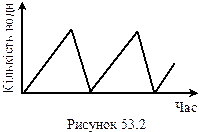Саме слово "релаксація" з грецького означає послаблення. Прикладом релаксаційних коливань в механіці може бути коливання посудини (рис.53.1), яка наповнюється водою. По мірі наповнення водою посудини її центр мас піднімається і стає вищим вісі обертання ОО. Посудина перевертається, вода виливається і посудина повертається в попереднє положення. Залежність кількості води від часу має характерну пилоподібну форму (рис.53.2), де перший повільний процес 1-2 це накопичення води, а другий 2-3 швидкий процес її зменшення, тобто релаксація (послаблення стану системи). В електриці роль нелінійного елемента, що зумовлює релаксаційні коливання, може грати неонова лампа, в якій і має місце нелінійна залежність сили струму в газі (неоні) від напруги (рис. 53.2). Тому, щоб зрозуміти принцип роботи релаксаційного генератора на неоновій лампі доцільно коротко зупинитись на окремих питаннях механізму провідності газів.

2. СТРУМ В ГАЗАХ. ВИДИ ГАЗОВИХ РОЗРЯДІВ.

Гази при звичайних умовах є діелектриками, в них відсутні вільні електричні заряди. Газ стає провідником струму, якщо деяка частина його молекул іонізується. Тобто від нейтральних молекул чи атомів відбираються електрони і тоді молекули (атоми) стають додатними іонами. Проходження струму через газ називається газовим розрядом Розрізняють несамостійний і самостійний газовий розряди. Несамостійний газовий розряд відбувається лише при постійній дії іонізатора. Іонізатором газу може бути термічна дія (нагрів газу), опромінювання ультрафіолетовим світлом, або радіоактивними частинками і т.п. Після припинення дії іонізатора несамостійний газовий розряд в газі припиняється.

Строго кажучи, провідність газів не завжди рівна нулю, так як в газах завжди присутня невелика кількість іонів і електронів завдяки дії природний радіоактивного випромінювання Землі, а також космічних променів. Саме така невелика кількість електронів і іонів зумовлює подальший розвиток самостійного газового розряду.

Розряд в газах, який продовжується після припинення дії іонізатора називається самостійним і він починається при певній напрузі - напрузі пробою (для неонової лампи - це напруга запалювання). Так, якщо в газі між двома електродами (катодом і анодом) створити електричне поле, то лише при певній напрузі електрони набувають енергії необхідної для іонізації молекул газу. Утворюються вторинні електрони та іони, які знову іонізують молекули газу і т.д. Такий процес має лавиноподібний характер який називається ударною іонізацією. Але ударна іонізація ще недостатня для підтримання самостійного розряду, необхідно, щоб електронні лавини "відтворювались". Це відтворення відбувається за рахунок додатних іонів, які прискорені електричним полем, вдаряючись об катод, вибивають з нього електрони. Крім того, мають місце ще інші процеси, а саме: 1) позитивні іони переводять в збуджений стан молекули газу, що супроводжується випусканням фотонів (газ світиться); 2) утворені фотони вибивають електрони з катода (фотоефект); 3) під дією фотонів можлива фотонна іонізація газу.

Якщо тиск в газах незначний (декілька мм.рт.ст.), то самостійний газовий розряд, приймає форму тліючого розряду. Саме такий розряд і спостерігається в неоновій лампі.

При більш високих тисках, наприклад, при атмосферному, розряд приймає форму іскрового. Іскри являють собою канали, які заповнені плазмою (іонізованим газом). Ці канали називаються стримерами (від англійського – стрічка). Прикладом іскрового розряду є таке природне явище, як блискавка.

Крім того, в газах можливі ще інші види розрядів - дуговий та коронний. Дуговий розряд підтримується за рахунок високої температури катоду, що приводить до інтенсивної термоелектронної емісії, а також за рахунок термічної іонізації молекул газу. Дуговий розряд широко застосовується для зварювання і різки металів.

Коронний розряд - високовольтний розряд в різко неоднорідному електричному полі. Наприклад, коли напруженість поля біля гострого вістря досягає 30 кВ/см, то біля цього вістря виникає свічення газу, яке має вигляд, корони, звідси назва - коронний розряд.

3. РЕЛАКСАЦІЙНИЙ ГЕНЕРАТОР НА НЕОНОВІЙ ЛАМПІ.

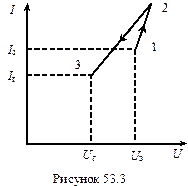Неонова лампа - газорозрядний прилад, конструктивно виконаний у вигляді скляного балона заповненого неоном при невеликому тиску (10-15 мм.рт.ст.). В балон впаяні два електрода, розташованих на відстані 1-3 мм. Характерною властивістю неонової лампи є те, що вона починає проводити струм при певному значенню напруги між електродами і ця напруга називається напругою запалювання U_з. При цій напрузі має місце самостійний розряд в неоні у вигляду тліючого розряду. Напруга запалювання залежить від відстані між електродами, їх форми, а також від тиску і природи газу. Після запалювання лампа може світитись при більш низькій напрузі і гасне при напрузі U_г (напруга гасіння). Вольт-амперна характеристика неонової лампи приведена на рис. 53.3. При малих напругах між електродами струм через лампу відсутній, при досягненні напруги запалювання в лампі виникає самостійний розряд і струм стрибком досягає значення I_з (струм запалювання). При подальшому збільшенні напруги (ділянка 1‑2) струм в лампі зростає (явища насичення не розглядаємо).

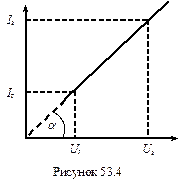Якщо зменшувати напругу, то зменшення струму характеризується ділянкою 2-3 (яка близька до ділянки 1-2)

При досягненні напруги U_г, яку називаються напругою гасіння, струм через лампу стрибком спадає до нуля і лампа гасне.

Для спрощеного математичного опису релаксаційного генератора на неоновій лампі користуються ідеалізованою вольт-амперною характеристикою лампи (рис. 53.4), де ділянки 1‑2 та 2‑3 співпадають. У відповідності з цією характеристикою внутрішній опір лампи R_i є розривною функцією від напруги U. Дійсно, при збільшенні напруги від нуля до напруги запалювання U_з опір лампи дорівнює нескінченості R_i = ¥ (струм відсутній). В області значень U > U_з опір лампи має певне кінцеве значення, яке згідно закону Ома дорівнює 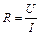. Значення цього опору чисельно дорівнює ctg a (рис. 53.4).

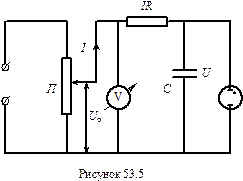Принципова схема релаксаційного генератора на неоновій лампі наведена на рис. 53.5. Паралельно до неонової лампи приєднаний конденсатор ємністю С, який заряджається через резистор опором R від джерела постійного струму. Напруга між обкладинками конденсатора вимірюється вольтметром і регулюється потенціометром П.

При вмиканні кола спочатку відбувається зарядка конденсатора (неонова лампа не горить). Закон зміни напруги на конденсаторі при його зарядці можна знайти, застосовуючи другий закон Кірхгофа для контуру RC.

iR + U =U_o , (53.1)

де iR - напруга на резисторі при значенні струму i, U - напруга на конденсаторі, U_o - напруга джерела струму (напруга на виході потенціометра). Так, як миттєве значення сили струму дорівнює

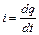, (53.2)

а з означення ємності конденсатора 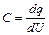- маємо

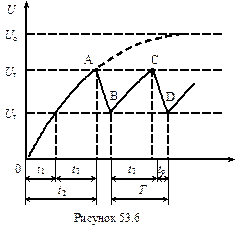
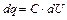(53.3)

то отримаємо рівняння

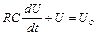(53.4)

Розв'язком такого рівняння за початкових умов U = 0 при t = 0 буде функція

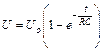(53.5)

Як видно з (53.5) напруга на конденсаторі асимптотично наближається до значення U_o (крива ОА, рис.53.6). Але раніше, ніж напруга U досягне значення U_o , лампа загориться. Спалах лампи відбувається при напрузі U = U_з і при цьому її опір стрибком змінюється від R = ¥ до R = const.

Якщо опір R настільки великий, так, що струм, який підводиться від джерела, значно менший розрядного струму через лампу, то конденсатор розряджається (крива АВ). В той момент, коли U стане рівна U_г , лампа гасне і конденсатор знову починає заряджатись. Напруга на ньому зростає по кривій ВС, а потім знову відбувається розрядка (крива CD) і т.д., тобто процес буде періодично повторюватись.

Визначимо період таких релаксаційних коливань. Період Т таких коливань складається з часу зарядки конденсатора t_з та часу його розрядки t_р

Т = t_з + t_р (53.6)

Час зарядки конденсатора , як видно з рис. 53.6, можна визначити через різницю

t_з = t₂ - t₁ (53.7)

де t₂ - час зарядки конденсатора до напруги U_з , t₁ - час зарядки конденсатора до напруги U_г.

В свою чергу значення t₂ і t₁ можна визначити за формулою 53.5

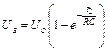(53.6)

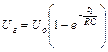(53.7)

звідки

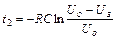(53.8)

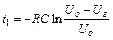(53.9)

Тому

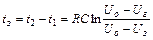(53.10)

Якщо опір резистора R значно більший опору лампи R_і , то час зарядки конденсатора t_з буде значно більший часу розрядки t_р і тому період релаксаційних поливань можна вважати приблизно рівним T= t_з , тобто

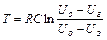(53.11)

4. ПРИНЦИП ЕКСПЕРИМЕНТАЛЬНОГО МЕТОДУ.

З формули 53.11 випливає, що величина 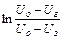є стала для даної неонової лампи, а період релаксаційних коливань пропорційний опору R резистора та ємності С конденсатора. Тому визначивши сталу лампи і вимірявши період Т релаксаційних коливань та знаючи ємність С з формули 53.11, можна отримати вираз для розрахунку невідомого опору:

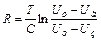. (53.12)

Аналогічно за відомим значенням опору R можна визначити невідому ємність

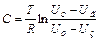
Якщо ж в нашому розпорядженні одночасно є відомій опір R_o та відома ємність C_o , то експериментальне визначення R_ox та невідомих ємностей C_x , за допомогою релаксаційного генератора на неоновій лампі можна звести до порівняння відповідних періодів релаксаційних коливань. Якщо при відомому опорі R_o період коливань буде рівним T_o, а при невідомому опорі R_x - Т, то як випливає з 53.12

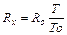(53.13)

Так само методом порівняння можна визначити невідому ємність

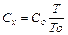(53.14)

де C_o - відома ємність, Т_о - період коливань генератора при відомій ємності, Т - при невідомій.

5. ОЦІНКА ПОХИБОК ЕКСПЕРИМЕНТУ.

Нехай при відомому опорі R_o за час t_o відбудеться N_o спалахів лампи, тоді період коливань Т_о буде рівним 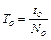. Якщо при невідомому опорі за час t лампа спалахне N разів, тоді період коливань буде рівним 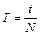. Тому робоча формула для визначення невідомого опору прийме вигляд

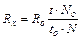(53.15)

Аналогічний вираз отримаємо і для визначення невідомої ємності

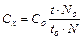(53.16)

Якщо робочі формули логарифмувати, а отриманий результат диференціювати, то отримаємо формули похибок

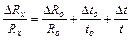(53.17)

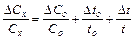(53.18)

(в числі спалахів не помиляємось, тобто похибки числа спалахів рівні нулю).

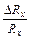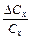З даних формул випливає, що точність шуканої величини (відносні похибки або ) визначається точністю еталонних величин (відомих опорів або ємностей, а також точністю вимірювань часу).

В даній роботі в якості еталонних опорів та ємностей використовуються резистори та ємності заводського виготовлення з відносною похибкою 4 % ,тобто 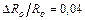і 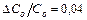. Тому відносна похибка вимірювань періоду релаксаційних коливань в сумі теж не повинна перевищувати 4 % .

Для вимірювання часу використовуємо секундомір. Ми ніколи точно не включимо і не зупинимо секундомір в моменти початку і кінця підрахунку спалахів лампи. Враховуючи суб'єктивний фактор, похибка вимірювання часу може складати величину порядку 0,4 с (0,2 с вмикання секундоміра, 0,2 с – зупинка) так, як відносна похибка часу одного вимірювання не повинна перевищувати 2%.

Таким чином в даній роботі слід визначати таке число спалахів, загальна тривалість яких повинна бути не менша, ніж 20 с.