Система дифференциальных уравнений Навье - Стокса
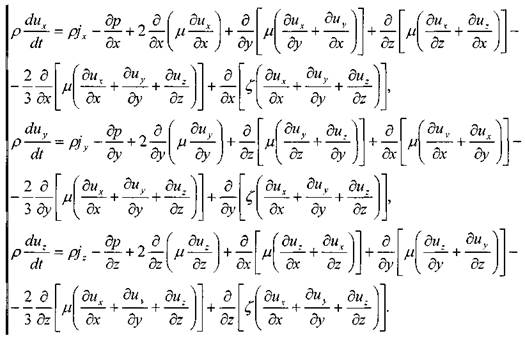
При 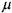 = const и
= const и 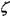 = const система уравнений значительно упростятся:
= const система уравнений значительно упростятся:
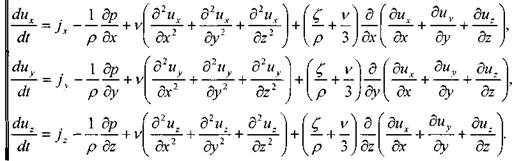
Пренебрегая величинами вторых вязкостей 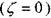 и считая жидкость несжимаемой
и считая жидкость несжимаемой
(р = const), уравнения Навье - Стокса запишутся в следующем виде:
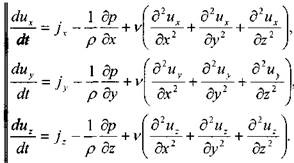
К уравнениям Навье - Стокса в качестве дополнительного уравнения принимается уравнение неразрывности. Учитывая громоздкость и трудность прямого решения задачи в практической деятельности (в случаях, когда это считается допустимым) решение достигается первым методом (по аналогии с движением идеальной жидкости).
5.2. Уравнение Бернуллидля элементарной струйки вязкой жидкости
Выделим в элементарной струйке жидкости двумя сечениями 1 - 1 и 2 - 2 отсек жидкости. Отсек жидкости находится под действием сил давления  и сил тяжести на жидкость в отсеке действуют также силы инерции самой движущейся жидкости, а также силы трения, препятствующие перемещению
и сил тяжести на жидкость в отсеке действуют также силы инерции самой движущейся жидкости, а также силы трения, препятствующие перемещению 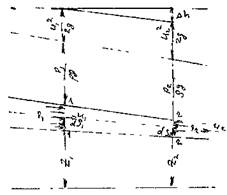 жидкости. В результате действия сил внутреннего трения часть механической энергии жидкости расходуется на преодоление возникающих сопротивлений. По этой причине величины гидродинамических напоров в сечениях будут неодинаковы. Естественно, что
жидкости. В результате действия сил внутреннего трения часть механической энергии жидкости расходуется на преодоление возникающих сопротивлений. По этой причине величины гидродинамических напоров в сечениях будут неодинаковы. Естественно, что 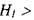 //2 .Тогда разность гидродинамических напоров в крайних сечениях отсеков
//2 .Тогда разность гидродинамических напоров в крайних сечениях отсеков 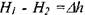 будут как раз характеризовать потери напора на преодоление сил трения. Эта величина носит название потерь напора на трение
будут как раз характеризовать потери напора на преодоление сил трения. Эта величина носит название потерь напора на трение 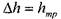
В этом случае уравнение Бернулли примет следующий вид:
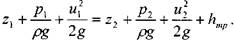
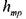 - потери удельной энергии (преобразование потенциальнойэнергии жидкости в тепловую энергию при трении).
- потери удельной энергии (преобразование потенциальнойэнергии жидкости в тепловую энергию при трении).
Величина 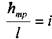 носит название гидравлического уклона.
носит название гидравлического уклона.
Дата добавления: 2016-05-31; просмотров: 2279;











