Расчеты на прочность и жесткость при растяжении (сжатии)

Одна из основных задач сопротивления материалов – подобрать размеры деталей, обеспечивающие прочность и жесткость этих деталей, подверженных тому или иному силовому, температурному или другому воздействию. Указанные размеры можно определить из расчета на прочность или жесткость. Рассмотрим условия прочности и жесткости для случаев простого растяжения (сжатия). Опасность наступления разрушения характеризуется величинами наибольших нормальных и касательных напря­жений, возникающих при нагружении в опасных (т. е. наиболее напряжен­ных) точках сечения. Очевидно, что реальные материалы не могут выдерживать сколь угодно большие напряжения. Поэтому величины наибольших напряжений из условия надежности работы детали необходимо ограничивать некоторыми допустимыми значениями, такими, чтобы деталь испытывала только упругие деформации. Их называют допускаемыми напряжениями. При растяжении и сжатии допускаемые напряжения обозначают [ 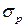], [ ] соответственно.

Если из расчета известны максимальные и минимальные (по алгебраической величине) напряжения, возникающие в опасном сечении детали, то условия прочности могут быть записаны следующим образом:

; .

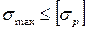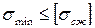Если материал одинаково сопротивляется растяжению и сжатию, что характерно для пластичных материалов (более строго для материалов в пластичном состоянии), а значит

,

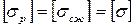(2.15)

и условие прочности при растяжении (сжатии) запишем в виде:

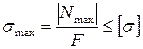. (2.16)

В некоторых случаях для обеспечения нормальной работы машин и сооружений размеры их деталей нужно выбирать так, чтобы обеспечивалось условие жесткости, то есть ограничить предельные деформации (перемещения) элементов конструкции.

Условие жесткости, ограничивающее изменение длины элемента, имеет следующий общий вид: ,

где 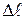- изменение размеров детали;

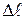[ ]- допускаемая величина этого изменения.

Учитывая, что при растяжении (сжатии) абсолютное удлинение в общем виде определяется как алгебраическая сумма величин 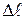по участкам

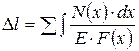, (2.17)

условие жесткости при растяжении (сжатии) запишем следующим образом:

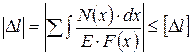. (2.18)