Перемещения и деформации при растяжении (сжатии)
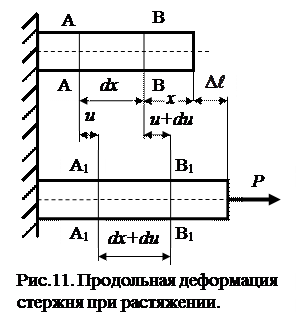 Рассмотрим стержень, находящийся под действием растягивающей нагрузки. Выделим (до деформации) двумя произвольными сечениями А-А и В-В бесконечно малый участок длиной dx на расстоянии x от свободного конца. Под действием внешней силы P сечение А-А переместиться в положение А1-А1 на расстояние u, а сечение В-В - в положение В1-В1 на расстояние u+du (du - бесконечно малая величина) Следовательно, абсолютное удлинение отрезка dx равно разности его размеров до и после деформации Δdx = du.
Рассмотрим стержень, находящийся под действием растягивающей нагрузки. Выделим (до деформации) двумя произвольными сечениями А-А и В-В бесконечно малый участок длиной dx на расстоянии x от свободного конца. Под действием внешней силы P сечение А-А переместиться в положение А1-А1 на расстояние u, а сечение В-В - в положение В1-В1 на расстояние u+du (du - бесконечно малая величина) Следовательно, абсолютное удлинение отрезка dx равно разности его размеров до и после деформации Δdx = du.
Относительная продольная деформация точек сечения А-А стержня при растяжении
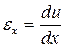 (2.5)
(2.5)
Для линейно-упругого матери-ала связь между нормальными напряжениями и относительной деформацией при растяжении определяется законом Гука:
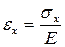 , (2.6)
, (2.6)
или, учитывая, что 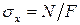 ,
,
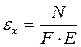 , (2.7)
, (2.7)
где Е - модуль нормальной упругости (модуль Юнга), постоянный коэффициент, который является константой материала (например, для стали Е=2∙1011 Па, для меди Е=1,2∙1011 Па, для титана Е=1,2∙1011 Па).
Исходя из этих формул, можно записать выражение для перемещений точек растягиваемого стержня в рассматриваемом сечении
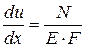 ,
,  , (2.8)
, (2.8)
Тогда полное удлинение стержня при растяжении 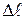 , равное перемещению точек правого крайнего сечения, относительно левого крайнего:
, равное перемещению точек правого крайнего сечения, относительно левого крайнего:
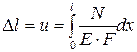 (2.9)
(2.9)
При постоянстве величин N, F, Е вдоль оси стержня, абсолютное удлинение можно найти так:
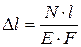 . (2.10)
. (2.10)
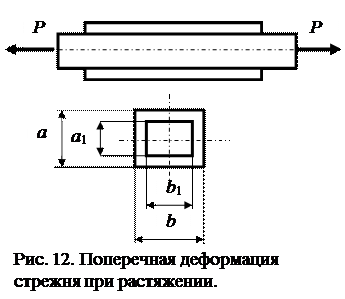
При растяжении стержень деформируется не только в продольном направлении, но и в поперечном.
Абсолютная поперечная деформация стержня опреде-ляется как разность его поперечных размеров до и после деформации:
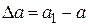 ;
;
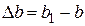 .
.
Относительная поперечная деформация стержня определяется отношением абсолютной поперечной деформации к соответствующему первоначальному размеру.
Относительная поперечная деформация при растяжении (сжатии) для изотропных материалов во всех направлениях одинакова:
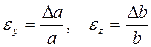 (2.11)
(2.11)
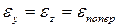 .
.
Между относительной поперечной и продольной деформациями прирастяжении (сжатии) в пределах применимости закона Гука существует постоянное соотношение, которое называется коэффициентом поперечных деформаций (коэффициентом Пуассона µ).
Коэффициент Пуассона равен абсолютной величине отношения поперечной деформации к продольной
 . (2.12)
. (2.12)
Коэффициент Пуассона – безразмерная величина.
Так как продольная и поперечная деформация для конструкционных материалов имеют противоположные знаки, можем записать
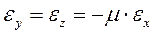 (2.13)
(2.13)
или, учитывая, что, согласно закону Гука, 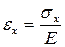 запишем
запишем
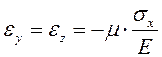 (2.14)
(2.14)
Коэффициент Пуассона µ также как и модуль Юнга Е характеризует упругие свойства материала. Для изотропных материалов коэффициент Пуассона находится в пределах от 0 до 0,5 (сталь 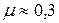 ; каучук
; каучук 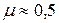 ).
).
Дата добавления: 2016-09-26; просмотров: 3138;











