Пусть сигнал на входе преобразователя описывается соотношением

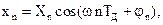
где X_n и φ_n – изменяющиеся во времени амплитуда и фаза входного сигнала соответственно, ω – частота сигнала.

Пусть на выходе генератора действует колебание вида

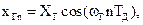
где X_Г – постоянная амплитуда, ω_Г – частота генерируемого колебания.

На выходе перемножителя действует сигнал

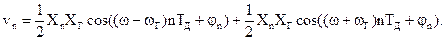
Если частотой выходного сигнала преобразователя является частота ω – ω_Г, то первое слагаемое описывает полезный продукт преобразования, а второе – побочный. Для удаления побочного продукта преобразования можно использовать или полосовой фильтр с центральной частотой полосы пропускания, равной ω – ω_Г, или ФНЧ, подавляющий составляющую частоты ω + ω_Г.

Поэтому выходной сигнал преобразователя равен

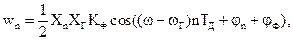
где K_Ф – коэффициент передачи фильтра для полезного продукта преобразования, 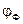-постоянный фазовый сдвиг, вносимый фильтром на частоте 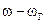. Полученное соотношение справедливо, если коэффициент передачи фильтра для побочного продукта преобразования равен нулю. В противном случае на выходе преобразователя будет действовать ослабленная составляющая на частоте ω + ω_Г.

Из последнего соотношения видно, что изменяющиеся во времени амплитуда и фаза выходного сигнала преобразователя частоты связаны линейными соотношениями с амплитудой и фазой входного сигнала. Это означает, что преобразование частоты не изменяет закона модуляции как при амплитудной, так и при угловой модуляции.

На рисунке 3.16 приведена схема квадратурного преобразователя частоты, содержащего 90-градусный фазорасщепитель и косинусно-синусный генератор.

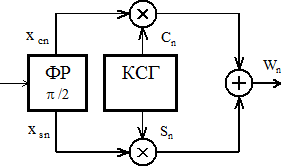
Рисунок 3.16 – Квадратурный преобразователь частоты

Пусть на выходах фазоращепителя действуют две квадратурные составляющие входного сигнала

Пусть на выходах косинусно-синусного генератора существуют колебания

Тогда выходной сигнал преобразователя определится соотношением

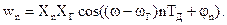
Таким образом, в случае идеальных ФР и КСГ на выходе преобразователя получается только полезный продукт преобразования. При наличии погрешностей этих узлов наряду с полезным продуктом преобразования будет существовать ослабленный побочный продукт преобразования.

3.7. Амплитудные детекторы

3.7.1.Амплитудный детектор - выпрямитель

Амплитудный детектор предназначен для формирования выходного сигнала, повторяющего закон изменения амплитуды входного сигнала.

На рисунке 3.17 дано графическое представление алгоритма функционирования цифрового амплитудного детектора – выпрямителя. Детектор состоит из блока определения абсолютного значения отсчета входного сигнала ABS и фильтра нижних частот.

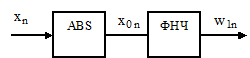
Рисунок 3.17 – Амплитудный детектор-выпрямитель

Пусть на входе детектора действует АМ сигнал

,

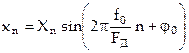где 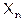- амплитуда входного сигнала, изменяющаяся во времени в процессе модуляции, 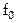- частота несущей, 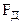- частота дискретизации, n – порядковый номер отсчета, 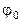- начальная фаза несущей.

Выходной сигнал блока ABS описывается следующим соотношением

.

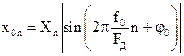Из последнего соотношения следует, что для получения сигнала, повторяющего закон изменения амплитуды 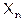, нужно выделить постоянную составляющую функции

.

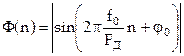Поэтому необходим фильтр нижних частот. Достоинством детектора-выпрямителя является его простота, а недостатком – зависимость постоянной составляющей функции 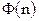от .

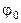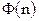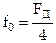На рисунке 3.18 показана функция при и 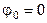. Из него видно, что постоянная составляющая этой функции дискретного времени равна 0.5.

Рисунок 3.18 – Функция Ф(n) пр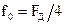и и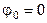

На рисунке 3.19 приведена та же функция, но при 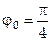. Из него видно, что постоянная составляющая равна 0.707.

Рисунок 3.19 - Функция Ф(n) пр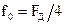и и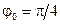

Таким образом, при частоте несущей, равной четверти частоты дискретизации, изменение начального фазового сдвига несущей от нуля до 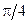изменяет величину постоянной составляющей функции 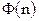более чем на 40%.

Следовательно, выходной сигнал детектора оказывается зависящим не только от амплитуды входного сигнала, но и от фазы несущей, что приводит к паразитной амплитудной модуляции сигнала.

Можно показать, что при частоте несущей, равной 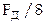, величина постоянной составляющей 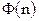изменяется при изменении фазы несущей не более чем на 8%.

Поэтому амплитудный детектор-выпрямитель целесообразно использовать только при частотах несущей, которые существенно меньше частоты дискретизации.

3.7.2.Квадратурный амплитудный детектор с блоком извлечения

квадратного корня

На рисунке 3.20 приведена схема квадратурного амплитудного детектора с блоком извлечения квадратного корня

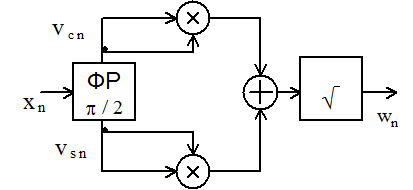
Рисунок 3.20 – Амплитудный детектор с блоком извлечения квадратного корня

В состав детектора входит 90-градусный фазорасщепитель (ФР), блок извлечения квадратного корня, два перемножителя и сумматор.

В случае идеального фазорасщепителя АМ сигналы на его выходах определяются соотношениями

.

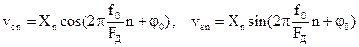Из схемы следует, что выходной сигнал детектора равен 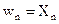и не зависит от частоты и фазы несущей, что является достоинством детектора. Недостаток детектора – наличие блока извлечения квадратного корня, требующего существенных программных затрат при микропроцессорной реализации детектора.

3.7.3. Синхронный амплитудный детектор с управляемым косинусно-синусным

генератором

Алгоритм функционирования синхронного амплитудного детектора с управляемым косинусно-синусным генератором приведен на рисунке 3.21. В состав детектора входят 90-градусный фазорасщепитель (ФР) и управляемый косинусно-синусный генератор (УКСГ), выполненный на основе генератора пилообразных колебаний. Частота пилы задается переменной

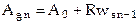, (3.3)

где 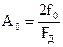- константа, задающая частоту УКСГ, равную частоте несущей входного АМ сигнала, R – константа управления.

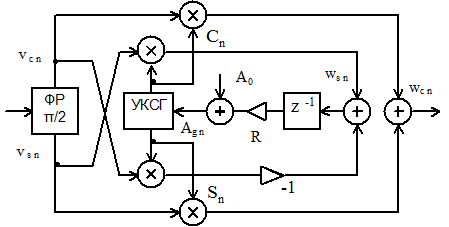
Рисунок 3.21 – Синхронный амплитудный детектор с управляемым КСГ

Текущий отсчет пилы на ее возрастающем участке определяется соотношением

.

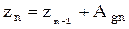Отсчет пилы определяет значения отсчетов косинусной и синусной компонент УКСГ

,

где X_Г – амплитуда генерируемых колебаний.

На выходах фазорасщепителя действуют две квадратурные компоненты детектируемого АМ сигнала

, .

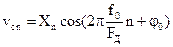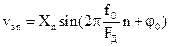Из рисунка 3.21 следует, что

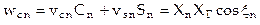, (3.4)

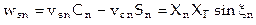
где 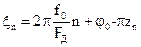. –мгновенная разность фаз соответствующих компонент входного сигнала и УКСГ

Приращение мгновенной разности фаз за один отсчет равно

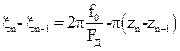
Согласно (3.3) 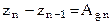, поэтому

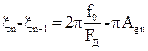. (3.5)

Согласно схеме рисунка 3.21

.

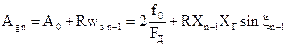Подставляя последнее соотношение в (3.5), получим

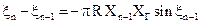
Последнее соотношение выражает связь мгновенной разности фаз с ее приращением и позволяет определить значение 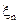в установившемся режиме. Зависимость 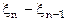от 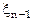приведена на рисунке 3.22.

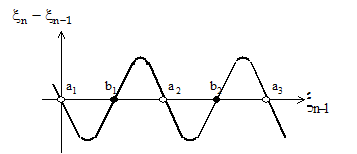
Рисунок 3.22 – Фазовый портрет кольца фазовой автоподстройки частоты

Синусоида с амплитудой 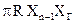пересекает ось абсцисс в точках а₁, а₂, а₃ ..., b₁, b₂ ... Точки «а» являются точками устойчивого равновесия, т.к. любому увеличению 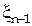по сравнению со значением в этой точке соответствует отрицательное значение ее приращения 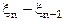, а уменьшению 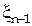– положительное значение ее приращения. В точках «b» всякому увеличению 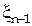соответствует ее положительное приращение, приводящее к дальнейшему возрастанию 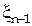до достижения ближайшей точки «а». Аналогичная ситуация возникает при уменьшении 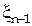по сравнению со значением в точке «b».

Из рисунка видно, что в точках «а» 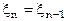, а значения 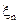равны 0, 2p, 4p и т.д., при которых 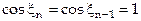. Поэтому согласно (3.4) выходной сигнал детектора равен

.

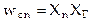Последнее соотношение показывает, что выходной сигнал детектора прямо пропорционален амплитуде входного сигнала, что и требуется для амплитудного детектирования.

Достоинством данного детектора являются малые нелинейные искажения выходного сигнала.

3.8. Фазовые детекторы

3.8.1.Фазовый детектор с выходным ФНЧ

Фазовый детектор предназначен для формирования выходного сигнала, зависящего от разности фаз входного сигнала и опорного колебания.

На рисунке 3.23 показан фазовый детектор, содержащий перемножитель, опорный генератор синусоидальных колебаний ОГ и ФНЧ.