Электропроводность металлических сплавов

В металлических сплавах концентрация носителей также не зависит от температуры. Поэтому температурная зависимость электропроводности сплавов целиком определяется е i зависимостью подвижности носителей от температуры. Рассмотрим этот вопрос более подробно.

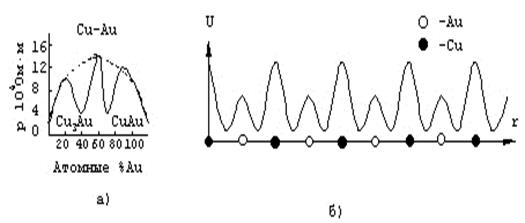
Предположим, что в идеальной решетке металла, например меди имеющей строго периодический потенциал U (рис. 2.2.1, а), часть узлов беспорядочно замещена атомами другого элемента, например золота. Так как потенциал поля примесных атомов отличен от потенциала основных атомов, то потенциал решетки не сохранится строго периодическим (рис. 2.2.1, б). Он нарушается беспорядочно распределенными примесными атомами. Такое нарушение приводит, естественно к рассеянию носителей и дополнительному электрическому сопротивлению.

	Рис 2.2.1 Потенциальная диаграмма для: а- идеальной решетки; б-решетки с примесями

Как показал Л. Нордгейм, в простейшем случае бинарных сплавов типа твердых растворов подвижность носителей, обусловленная рассеянием их на нарушениях решетки, определяется следующим приближенным соотношением:

m _спл ~ ω(1 - ω),(6.302.2.1)

где ω и (1 - ω) — относительные доли металлов, образующих сплав.

Подставив m_спл из (6.302.2.1) в (6.122.1.1) и помня, что ρ = 1/ g, получим

следующее выражение для удельного сопротивления бинарного сплава:

ρ_спл=β[ω(1 - ω)], (2.2.26.З1)

где β — коэффициент пропорциональности.

Функция ω (1 - ω)имеет максимум при ω = 1/2, т. е. при равном содержании в сплаве обеих компонент. В качестве примера на рис. 2.2.2, а показана зависимость удельного сопротивления сплавов меди с золотом от содержания золота. Кривая проходит через максимум, отвечающий 50% меди и золота в сплаве.

	Рис 2.2.2, а - зависимость удельного сопротивления сплава от примеси; б-потенциальная диаграмма решетки сплава

Из рис. 2.2.2, а видно далее, что абсолютное значение ρ_спл значительно выше ρ чистых компонент. Так, при комнатной температуре ρ_Cu = 1,7×10^-8 Ом×м, ρ_Au = l,56×10^-8 Ом×м, а ρ_{50%Cu. + 50%Au} =15×10^-8Ом×м. Это вполне естественно, так как примеси вызывают значительно более сильное нарушение периодичности потенциала решетки, чем тепловые колебания. Если, однако, сплавляемые металлы при определенном соотношении компонент образуют металлическое соединение с упорядоченной внутренней структурой, то периодичность потенциала решетки восстанавливается (рис. 2.2.2, б) и сопротивление, обусловленное рассеянием на примесях, практически почти полностью исчезает. Для сплавов меди с золотом это имеет место при соотношении компонент, отвечающем стехиометрическому составу Cu₃Au и CuAu (рис. 2.2.2, а, сплошные кривые). Это является убедительным подтверждением квантовой теории электропроводности, согласно которой основной причиной электрического сопротивления твердых тел является не столкновение свободных электронов с атомами решетки, а рассеяние их на дефектах решетки, вызывающих нарушение периодичности ее потенциала.

Идеально правильная, бездефектная решетка, имеющая строго периодический потенциал, не способна рассеивать свободные носители заряда и поэтому должна обладать нулевым сопротивлением. Это подтверждается многочисленными опытами с предельно чистыми металлами в области низких температур, в частности данными табл. 2.1.2: по мере повышения степени чистоты металлов их сопротивление вблизи абсолютного нуля непрерывно падает, стремясь к нулю. Подчеркнем, что это не явление сверхпроводимости, о котором будет речь впереди, а естественное поведение всех абсолютно чистых металлов при предельно низких температурах, вытекающее из квантовой природы электрического сопротивления.

При небольшом содержании примеси в (6.312.2.2) можно положить (1 - ω)»1 . Тогда ρ_спл ~ ω. Это удельное сопротивление не зависит от температуры и сохраняется при абсолютном нуле. Его называют остаточным сопротивлением ρ_ост= ρ_П (см. рис.2.1.3).

При температуре, отличной от абсолютного нуля, к остаточному сопротивлению присоединяется сопротивление ρ_Т, обусловленное рассеянием на тепловых колебаниях решетки, и общее удельное сопротивление равно

ρ = ρ_П + ρ_Т. (6.322.2.3)

Это соотношение выражает известное правило Матиссена об аддитивности удельного сопротивления.

Рассмотрим теперь температурный коэффициент сопротивления a. Как известно, он выражает относительное изменение удельного сопротивления проводника ρ при нагревании его на 1 °К. Так как для чистых металлов ρ= ρ_Т, то

(6.332.2.4)

Как показывает опыт, грубо

[см. табл. (2.2.1)]. Для сплавов ρ = ρ_П + ρ_Т, поэтому

так как ρ_П от температуры не зависит. Это выражение можно преобразовать следующим образом:

, (6.342.2.5)

где a— температурный коэффициент сопротивления чистых металлов.

Из (6.342.2.5) видно, что α _спл должен быть меньше α чистого металла, причем тем меньше, чем больше ρ_П по сравнению с ρ_Т . Обычно ρ_П на порядок и более выше ρ_Т , поэтому α _спл может быть на порядок и более ниже a чистого металла, что в основном подтверждается опытом (табл. 2.2.1; данные приведены для комнатной температуры).

Табл.2.2.1

Однако во многих случаях температурная зависимость сопротивления сплавов является значительно более сложной, чем та, которая вытекает из простой аддитивной закономерности (6.322.2.3), и температурный коэффициент сопротивления сплавов может быть много меньше, чем можно было бы ожидать согласно (6.342.2.5). Более того, он не остается постоянным в широком интервале температур, а в ряде случаев является даже отрицательным, как это имеет место, например, у константы (табл. 2.2.1) и у некоторых других сплавов.

Высокое удельное сопротивление и низкий температурный коэффициент сопротивления сплавов открыли для них широкие возможности практического применения для изготовления разнообразных проволочных и пленочных резисторов и переменных сопротивлений (реостатов), используемых в различных областях техники.