Электропроводность чистых металлов
Электропроводность чистых металлов обусловлена дрейфом свободных носителей заряда одного знака. В подавляющем большинстве чистых металлов такими носителями являются свободные электроны. Однако в ряде металлов, таких, например, как бериллий, цинк и некоторые другие., свободными носителями заряда являются дырки.
Проводимость электронных металлов описывается формулой:
g = qnm (6.122.1.1)
где n – концентрация носителей заряда;
m- подвижность носителей заряда.
Так как металлы являются вырожденными проводниками, то концентрация n электронного газа в них практически не зависит от температуры. Поэтому зависимость удельной электропроводности g от температуры полностью определяется температурной зависимостью подвижности mэлектронов вырожденного электронного газа. Это объясняется следующим образом.
Удельная электропроводность проводника
Зная скорость дрейфа электронов, легко вычислить плотность электрического тока и удельную электропроводность проводника. Для этого выделим внутри проводника цилиндр с основанием, равным единице, и образующей, равной 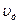 и направленной вдоль дрейфа (рис.2.1.1).
и направленной вдоль дрейфа (рис.2.1.1).
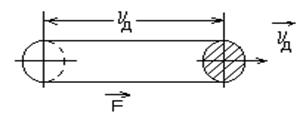
Рис.2.1.1 Схема элементарного участка проводника с током
Все электроны, заключенные в этом цилиндре, в течение 1 с. пройдут через основание и образуют ток плотностью
 ,
,
где m– подвижность носителей заряда.
Отсюда, согласно закону Ома  ,
, 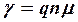 .
.
C учетом того, что 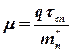 , а ;
, а ; 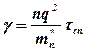 ,
,  ;
;
где tсп – время свободного пробега;
m*n- эффективная масса электрона;
 ;
;
где lcп – длина свободного пробега;
nстолкн – среднее количество столкновений с рассеивающими центрами;
u– средняя скорость движения электрона
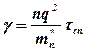 ...
...
Невырожденный газ
В случае невырожденного газа вероятность заполнения зоны проводимости электронами настолько небольшая, что они практически не встречаются так близко, чтобы их поведение могло ограничиваться принципом Паули. Электроны являются полностью свободными в том смысле, что на движение любого из них другие не оказывают никакого влияния. Поэтому все электроны проводимости невырожденного газа принимают практически независимое друг от друга участие в создании электрического тока и формировании электропроводности проводника. Поэтому для электропроводности невырожденного газа пользуются средними параметрами: средней длиной свободного пробега, средней скоростью движения и средним временем релаксации:
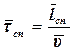 ;
;  ;
; 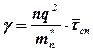 .
.
Вырожденный газ.
Для вырожденного газа все квантовые состояния ниже уровня Ферми заняты электронами. Поэтому внешнее поле может воздействовать лишь на электроны, расположенные около уровня Ферми, переводя их на более высокие свободные уровни. Это означает, что в вырожденном газе в формировании электропроводности могут участвовать не все свободные электроны, а лишь те из них, которые располагаются непосредственно у уровня Ферми. Поэтому в качестве времени релаксации в предыдущих формулах следует брать время релаксации электронов, обладающих энергией, практически равной энергии Ферми, т.е. tспF .
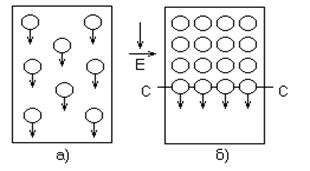
Рис.2.1.2 Схема, поясняющая движение носителей заряда:
а- невырожденный газ; б- вырожденный газ.
Для пояснения различия между поведением в электрическом поле невырожденного и вырожденного электрических газов можно привести грубую механическую аналогию. Представим, что на поверхности воды, налитой в плоский сосуд, плавают заряженные частицы-шарики, которые в отсутствии внешнего поля совершают беспорядочные движения с различными скоростями (рис.2.1.2, а). Если поместить сосуд во внешнее поле 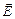 , то результат воздействия поля на “коллектив” шариков как целое будет существенно зависеть от того, как плотно они “уложены” на поверхности воды. Движение невырожденного коллектива определяется средними параметрами, а вырожденного определяется движением нижнего слоя частиц СС (рис.2.1.2, б). Для вырожденного электронного газа роль слоя выполняют электроны, располагающиеся у уровня Ферми.
, то результат воздействия поля на “коллектив” шариков как целое будет существенно зависеть от того, как плотно они “уложены” на поверхности воды. Движение невырожденного коллектива определяется средними параметрами, а вырожденного определяется движением нижнего слоя частиц СС (рис.2.1.2, б). Для вырожденного электронного газа роль слоя выполняют электроны, располагающиеся у уровня Ферми.
Определено, что носители заряда в металлах составляют вырожденный электронный газ. Удельная проводимость металлов определяется выражением
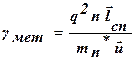 ,
,
где 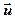 - средняя скорость движения электронов.
- средняя скорость движения электронов.
Поэтому, температурная зависимость удельного сопротивления металлических проводников при сравнительно высоких температурах будет зависеть от величины  , т.к. в металлах скорости движения носителей заряда различаются мало, поскольку свобода перемещения электронов ограничивается принципом Паули. В свою очередь, зависимость длины свободного пробега от температуры определяется выражением
, т.к. в металлах скорости движения носителей заряда различаются мало, поскольку свобода перемещения электронов ограничивается принципом Паули. В свою очередь, зависимость длины свободного пробега от температуры определяется выражением
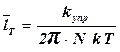 ,
,
где 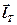 - длина свободного пробега, зависящая от температуры;
- длина свободного пробега, зависящая от температуры;
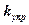 - коэффициент упругой связи, которая стремится вернуть атом в положение равновесия;
- коэффициент упругой связи, которая стремится вернуть атом в положение равновесия;
N – число атомов в единице объема материала.
С учетом изложенного, установлено, что подвижность носителей для невырожденного газа m ~ T-3/2 , а для вырожденного газа m ~ T-1, поэтому получены следующие выражения для удельной электропроводности g и удельного сопротивления ρ чистых металлов:
в области высоких температур (T > 200 °К)
g = A / T, ρ = аТ, (6.282.1.2)
в области низких температур
g= В/Т5 , ρ = bТ5. (6.292.1.3)
Здесь А, В, a, b— коэффициенты пропорциональности.
Табл.2.1.1
| Элемент | Na | K | Rb | Сu | Ag | Аu |
| g теор , 106 Ом –1 ×м-1 | ||||||
| g эксп , 106 Ом –1 ×м-1 |
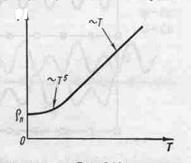
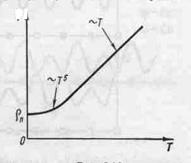
На рис.2.1.3 показана схематическая кривая зависимости удельного сопротивления чистых металлов от температуры. В области высоких температур графиком ρ (Т) является прямая, в области низких температур — парабола 5-й степени, и вблизи абсолютного нуля, где основное значение имеет рассеяние на примесях, — прямая, параллельная оси температур.
|
|

|

|

|

|
 |

Более строгий квантово-механический расчет позволяет вычислить коэффициенты А, а, В, bвв формулах (6.282.1.2) и (6.292.1.3). В табл. 2.1.1 приведена удельная электропроводность ряда чистых металлов при комнатной температуре, вычисленная теоретически (gтеор) и определенная экспериментально (g эксп )
Из данных этой таблицы видно, что согласие теории с опытом является удовлетворительным для Na и К, у которых состояние электронов проводимости близко к состоянию свободных электронов. С увеличением атомной массы металла увеличивается потенциал решетки, растет взаимодействие электронов проводимости с решеткой и приближение свободных электронов выполняется хуже. Поэтому наблюдается все большее расхождение между g теор и g эксп .
Табл.2.1.2
| Т, °К | 87,4 | 57,8 | 20,4 | 11,1 | 4,2 | |
| (g о / g )теор | 0,2645 | 0,1356 | 0,0060 | 0,0003 | 3 10-6 | |
| (g о / g )эксп | 0,2551 | 0,1314 | 0,0058 | 0,0003 | 3 10-6 |
В табл. 2.1.2 приведены отношения проводимости g о золота при 273 °К к проводимости gего gпри низких температурах, вычисленные теоретически и определенные экспериментально.
Как видно, согласие теории с опытом является вполне удовлетворительным.
Дата добавления: 2020-12-11; просмотров: 502;











