Коди з пошуком та коригуванням помилок
Використання більшої кількості бітів у кодових словах дає можливість зробити мінімальну кодову відстань більшою ніж 2, що відкриває можливість не тільки виявляти, а й виконувати корекцію спотворених кодових слів. Прикладом коду, який надає можливість легко виявити помилку в передачі, є подвійно-п’ятирічний код. Його значення приведені в табл. 3.1.
Старші два біти b6 b5 розділяють всі коди на дві групи: молодших десяткових чисел 0 – 4, які кодуються однаково b6 b5 = 01; старших десяткових чисел 5 – 9, які мають код b6 b5 = 10.
Молодші 5 розрядів формують коди 1 з 5. Як видно з таблиці, поява помилки в будь-якому біті такого коду легко може бути виявлена, а інформація буде визнана помилковою.
Таблиця 3.1.
| N | b6 | b5 | b4 | b3 | b2 | b1 | b0 |
Розглянемо тепер, як можна використовувати коди для корекції одиночних помилок або виявлення більшої їх кількості.
Допустимо, що код має мінімальну кодову відстань 3.
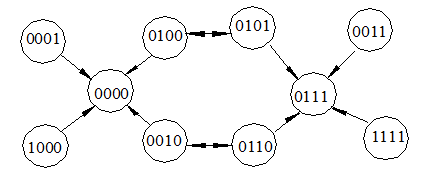
Рис.3.3.
Рис. 3.3 показує фрагмент n-вимірного кубу для такого коду з кодовими словами 0000 і 0111. При відстані 3 маємо три біти різниці між двома сусідніми вершинами кубу. Допустимо тепер, що передається інформація і при її передачі має місце помилка в одному біті. Якщо передається кодове слово 0000, то з помилкою можуть біти отримані слова, які на рис. 3.3 оточують вказане кодове слово. У такому випадку при появі одиночної помилки з’являються позакодові слова, які відрізняються від кодового слова лише на один біт. Вони не тільки легко можуть бути виявлені, а й виправлені, що відображено стрілками на рис. 3.3. Аналогічна картина має місце і стосовно другого кодового слова. Наприклад, створення позакодового слова 0101 з більшою ймовірністю відповідає кодовому слову 0111, ніж 0000.
Таким чином, при прийомі інформації необхідно приймати рішення, яке з кодових слів дійсно отримане. Таке рішення є операцією декодування з виправленням помилок, а відповідні апаратні засоби називаються декодерами з виправленням помилок. Коди, що використовуються для виправлення помилок при передачі інформації, називаються коригуючими.
Код Хемінга
У загальному плані, якщо код має відстань d = 2b + 1, то він може бути використаним для корекції помилок, що впливають на b бітів. Якщо ж коди мають мінімальну відстань d = 2b + c + 1, то вони можуть бути використані для корекції помилок у b бітах і виявляти помилки в c бітах.
Прикладом такого коду є код Хемінга. Він може бути створений для будь-якого цілого числа і, яке визначає код довжиною (2і – 1) біт з і розрядів парності і (2і – 1 – і) інформаційних розрядів з відстанню між кодовими словами 3.
Положення кожного розряду слова коду Хемінга нумерується від 1 до (2і – 1). Будь-який розряд з номером розміщення в слові, кратний 2, є бітом парності, решта – інформаційні. Кожен біт парності об’єднаний у групу з підконтрольними йому інформаційними бітами. Таке об’єднання зроблено в табл. 3.2.
Таблиця 3.2.
| Номер розряду | Контрольний розряд | |||||||
| Код розряду | ||||||||
| Група А | Х | Х | Х | Х | 20 ( 0 ) | |||
| Група В | Х | Х | Х | Х | 21 ( 1 ) | |||
| Група С | Х | Х | Х | Х | 22 ( 1 ) | |||
| Біти парності | 22 | 21 | 20 |
З табл. 3.2 бачимо, що бітами парності є розряди 1, 2, 4.
У коді кожного біта парності має місце лише одна одиниця, причому її місця у коді розряду різні – відповідно, у першому; другому; третьому. Одиниця біту парності об’єднує в групу ті розряди кодового слова, які мають одиниці у відповідному біті. Наприклад, до групи А об’єднані розряди кодового слова 1, 3, 5, 7, у яких містяться одиниці в першому коді розряду. Оскільки перший біт у цій групі є бітом парності, то решта – підлеглі йому біти, в яких забезпечується перевірка парності. Сформована таким шляхом таблиця, яка доповнена стовбцем контрольного розряду, називається матрицею перевірки парності.
З попереднього матеріалу ми бачили, що при кодовій відстані 3, яку забезпечує код Хемінга, два сусідні кодові слова відрізняються на три біти. Це означає, що зміна в кодовому слові одного або двох бітів призводить до того, що вони випадають з набору кодових слів, тобто стають позакодовими.
У табл. 3.3 приводиться перелік кодових слів для відстані 3 коду Хемінга з чотирма інформаційними бітами.
Таблиця 3.3.
| Інформаційні біти | Біти парності | Інформаційні біти | Біти парності | Інформаційні біти | Біти парності | Інформаційні біти | Біти парності |
Якщо при передачі інформації в j-му розряді кодового слова зміниться значення біта, то, відповідно, зміниться парність у кожній групі, що містить розряд j. Оскільки кожен інформаційний біт міститься по крайній мірі в одній групі, то по крайній мірі в одній групі буде порушена парність і визначена наявність позакодового слова.
Якщо ж у кодовому слові зміняться два розряди, то групи парності, що містять обидва розряди, не зможуть визначити помилку в слові, котре передається, оскільки парність порушена не буде. Але, оскільки біти з помилками можуть бути лише в різних розрядах, то їх представлення у групах також буде різним. Це означає, що в одній з груп буде представлений лише один з пошкоджених бітів. У такому випадку в цій групі контролем парності буде визначена наявність позакодового слова.
Розглянемо на конкретному прикладі особливості визначення позакодового слова і корекцію помилки.
Допустимо, що на приймальній стороні системи передачі інформації прийнято слово 0100111. Перевіримо це слово, в якому 7-й, 5-й і 4-й розряди мають нульові значення, за допомогою таблиці парності. Результати перевірки заносяться у контрольний розряд. Для групи А 7-й і 5-й розряди мають нульові значення, а 1-й і 3-й – одиниці. Тобто в групі маємо парну кількість одиниць і в контрольний розряд у відповідності з контролем парності заноситься нуль. Аналогічно, в групі В маємо одиниці в розрядах 6, 3, 2, тобто непарну їх кількість, і в контрольний розряд заноситься одиниця. Для групи С у розрядах 7, 6, 5, 4 маємо лише одну одиницю, і в контрольний розряд теж записуємо “1”.
У відповідності до вагових коефіцієнтів груп, у контрольному розряді записано в двійковому коді число 6, якому відповідає біт кодового слова з прийнятою помилкою. У шостому розряді кодового слова стоїть “1”, а повинен бути “0”. Апаратними засобами така помилка може бути виправлена.
Коди Хемінга з кодовою відстанню 3 і 4 знаходять широке використання для визначення і виправлення помилок у модулях пам’яті комп’ютерних систем великої ємності – наприклад, в мультипроцесорних системах і мейнфреймах. Привабливість їх використання в таких модулях обумовлена тим, що кількість бітів парності при зростанні розрядності довжини слова зростає в меншій мірі. Наприклад, при кількості інформаційних біт 4 кількість біт парності дорівнює 3, а при кількості інформаційних біт 26 кількість біт парності зростає до 5.
Двовимірні коди
Інший шлях отримання кодів з великою мінімальною кодовою відстанню – це використання двовимірних кодів. Інформаційні біти формуються у двовимірну матрицю і біт парності забезпечує перевірку рядків та стовбців. Код Cr з мінімальною кодовою відстанню dr використовується для перевірки рядків, а, відповідно, код Cc з мінімальною кодовою відстанню dc використовується для перевірки стовбців. Це означає, що біт парності вибирається так, що кожен рядок є кодовим словом у Сr , а кожен стовбець є кодовим словом у Сс . Мінімальна відстань двовимірного коду є функцією drі dc. Найпростіший двовимірний код використовує один біт парності по рядках і один по стовбцях і має мінімальну відстань 2 × 2 = 4. Це означає, що будь-яка помилка в 1, 2, 3 бітах призводить до появи непарності у рядку, стовбці або в обох одночасно. Невизначена помилка може мати місце лише при наявності помилок у чотирьох бітах.
Двовимірні коди використовуються для перевірки системи пам’яті персональних комп’ютерів, яким характерна двовимірна матрична структура n слів по m біт.
Контроль парності
Незважаючи на високу надійність та перешкодостійкість цифрових систем передачі інформації, вірогідність виникнення похибок завжди існує. Тому всі високонадійні канали передачі інформації забезпечуються допоміжними схемами, які дають можливість впевнитись в відсутності похибок. У будь-якій структурі каналу передачі інформації з контролем похибок повинна бути надмірність каналу. Наприклад, якщо передається код 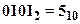 і на виході каналу з’являється
і на виході каналу з’являється 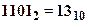 , то в загальному плані похибку без спеціальних перевірок визначити неможливо. Але, якщо ми знаємо, що інформація передається у двійково-десятковому коді, то одержаний результат хибний. Тобто, наявність шести надлишкових станів дає можливість виявити деякі похибки.
, то в загальному плані похибку без спеціальних перевірок визначити неможливо. Але, якщо ми знаємо, що інформація передається у двійково-десятковому коді, то одержаний результат хибний. Тобто, наявність шести надлишкових станів дає можливість виявити деякі похибки.
Простий спосіб визначення похибок в словах, які передаються, базується на припущенні, що найбільша вірогідність збою можлива тільки в одному біті, тобто при появі помилкової одиниці або нуля. Тому для визначення наявності такого збою використовують контроль парності або контроль непарності одиниць у переданому слові (Parity Check). В основі цього способу лежить операція знаходження суми за модулем 2 всіх двійкових розрядів контрольованого слова. При парній кількості одиниць вказана сума дорівнює 0, а при непарній – 1. Прикладом побудови такого пристрою контролю є схема, що приведена на рис. 3.4.
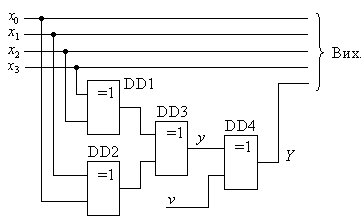 Рис.3.4.
Рис.3.4.
|
Таблиця 3.4.
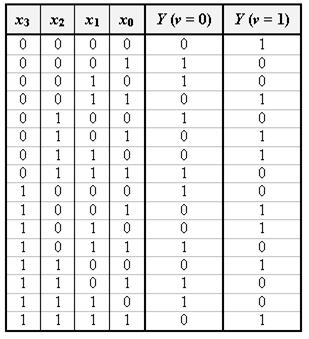
|
Сигнал на виході Y визначається наступною логічною функцією:
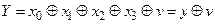 .
.
З аналізу роботи пристрою, схема якого приведена на рис. 3.46, витікає, що при парній кількості одиниць у слові 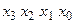 значення виходу
значення виходу 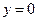 . При непарній –
. При непарній – 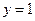 . Тому значення Y залежить від сигналу v, який задає режим контролю – контроль парності або контроль непарності.
. Тому значення Y залежить від сигналу v, який задає режим контролю – контроль парності або контроль непарності.
При контролі парності задається v = 0. Якщо відбудеться контроль за непарною кількістю одиниць, то задається v = 1 (див. табл. 3.4).
Вихід Y називається контрольним бітом. При прийомі інформації одержане слово знов перевіряється на парність або непарність. Якщо при контролі парності в приймальному контрольному пристрої з’явилась 1, то це значить, що або в інформаційній шині, або в контрольному біті з’явилась похибка. Як бачимо, такий простий контроль не дає можливості виправити похибку, але він дає можливість визначитись з хибною інформацією, щоб потім або використати її, або відкоригувати.
У практиці контролю переважно використовують спосіб контролю по непарності. Пов’язано це з тим, що при появі слова з усіма нулями при контролі по парності цю ситуацію неможливо буде відрізнити від обриву лінії зв’язку.
Приведена схема не може визначити подвійної похибки і будь-якої кількості парних похибок. Пояснюється це лише малою надмірністю лінії зв’язку. Тому для більш глибокого контролю необхідно мати і більшу її надмірність. Оскільки цифрові лінії зв’язку дуже надійні і ймовірність появи двох незалежних похибок 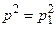 , тому навіть такий простий контроль суттєво піднімає надійність передачі інформації. Завдяки цьому цей вид контролю використовується практично в усіх каналах передачі цифрових даних, а також при роботі процесора з запам’ятовуючими пристроями, контролюючи тим самим і пристрої пам’яті.
, тому навіть такий простий контроль суттєво піднімає надійність передачі інформації. Завдяки цьому цей вид контролю використовується практично в усіх каналах передачі цифрових даних, а також при роботі процесора з запам’ятовуючими пристроями, контролюючи тим самим і пристрої пам’яті.
Корекція помилок
Розглянутий спосіб оцінки достовірності передачі інформації по каналу зв’язку не дає можливості знайти похибку в інформаційному слові. Тому в складних комп’ютеризованих та мікропроцесорних схемах з розгалуженими каналами цифрового зв’язку використовують системи передачі з використанням таких кодів, які дозволяють як знаходити, так і виправляти випадкові похибки. До них відносяться, наприклад, код Хемінга, циклічні коди, які використовуються для виявлення та виправлення похибок не тільки при передачі, але й при зберіганні даних; код Ріда-Соломона, який широко використовується при записі та зчитуванні компакт-дисків, та інші.
Розглянемо ідеологію та принцип побудови цифрових кодерів з виправленням похибок на прикладі використання коду Хемінга.
Припустимо, що необхідно визначити та виправити одиничну похибку двійкового коду з n інформаційними розрядами. До цього коду додається m контрольних кодів. В результаті одержуємо кількість символів у коді
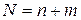 . .
| (3.1) |
При передачі кодів може бути спотвореним будь-який інформаційний сигнал. Але може виникнути й така ситуація, коли жоден з розрядів не буде спотворений, тобто, якщо в створеному коді маємо N розрядів, то за допомогою контрольних кодів, що входять, відповідно до (3.1), в це число, повинна бути створена така кількість комбінацій 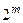 , щоб мати можливість закодувати будь-який з розрядів. Тому повинна виконуватись нерівність:
, щоб мати можливість закодувати будь-який з розрядів. Тому повинна виконуватись нерівність:
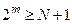
| (3.2) |
або відповідно до (3.1)
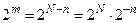 . .
| (3.3) |
З (3.2) з врахуванням (3.3) знаходимо:
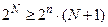 . .
| (3.4) |
З (3.4) знаходиться кількість інформаційних розрядів у кодованому слові з N розрядами:
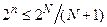 . .
| (3.5) |
Критерій оптимальності коду Хемінга має вигляд:
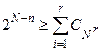 , ,
| (3.6) |
де 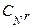 – кількість комбінацій з N по r ; r – кількість виявлених незалежних похибок.
– кількість комбінацій з N по r ; r – кількість виявлених незалежних похибок.
При 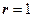 (тобто для одиничних похибок) формула (3.6) має вигляд:
(тобто для одиничних похибок) формула (3.6) має вигляд:
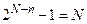 . .
| (3.7) |
Формула (3.7) є нижньою межею коду, адже встановлює те мінімальне співвідношення коригуючих та інформаційних розрядів, нижче якого код не може зберігати свої коригуючі здібності.
Як приклад, розглянемо ситуацію, коли слово має 11 розрядів 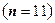 . У цьому випадку формула (3.5) перетворюється в рівність при
. У цьому випадку формула (3.5) перетворюється в рівність при 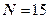 . Тобто кількість коригуючих розрядів
. Тобто кількість коригуючих розрядів 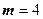 .
.
Пояснимо, що можливість виправлення похибки в коді Хемінга базується на повтореній k разів системі контролю парності, але не всього слова одночасно, а k окремих груп його розрядів. Слово розбивається на групи так, щоб номер кожного розряду визначався за його належністю до цих груп. Вказані групи називаються групами контролю парності і компонуються з розрядів кодового слова на основі наступних правил:
а) кожен розряд кодового слова кодується в відповідності до принципів перетворення десяткового коду в двійковий. Оскільки в нашому випадку 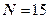 , то для кодування кожного розряду кодового слова необхідно мати
, то для кодування кожного розряду кодового слова необхідно мати 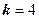 розряди двійкового коду. При цьому створюється
розряди двійкового коду. При цьому створюється 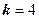 групи контролю парності;
групи контролю парності;
б) в кожну і-у контрольну групу входять ті розряди кодового слова, в двійковому номері яких в і-й позиції знаходиться одиниця. Ідеологія створення контрольних груп пояснюється рис. 3.5.
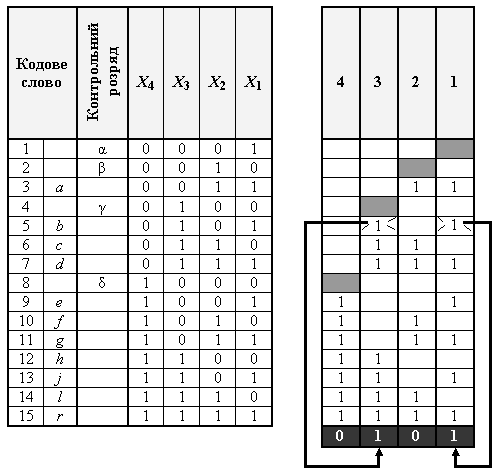
Рис.3.5.
Рис. 3.5 показує організацію кодованого блоку, який планується передавати по лінії зв’язку, – кодового слова. Воно має одинадцять розрядів інформаційного слова, розряди якого позначені малими латинськими літерами 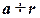 , та чотирьох контрольних розрядів, які позначені буквами грецького алфавіту a, b, g, d. Контрольні розряди розміщуються в масиві кодового слова, в клітках тих розрядів, в яких має місце одиниця тільки в одній позиції. Адресі вказаної одиниці i відповідає контрольний розряд.
, та чотирьох контрольних розрядів, які позначені буквами грецького алфавіту a, b, g, d. Контрольні розряди розміщуються в масиві кодового слова, в клітках тих розрядів, в яких має місце одиниця тільки в одній позиції. Адресі вказаної одиниці i відповідає контрольний розряд.
Відповідно до вказаних правил формування контрольних груп, 4-й розряд входить всього до однієї – третьої – групи; розряд 6 – до другої та третьої; розряд 10 – до другої та четвертої, i т. д. Тому четверта група включає в себе лише розряди від 8-го по 15-й, а третя 4-7 та 12-15. Наймолодший розряд кожної групи є контрольним.
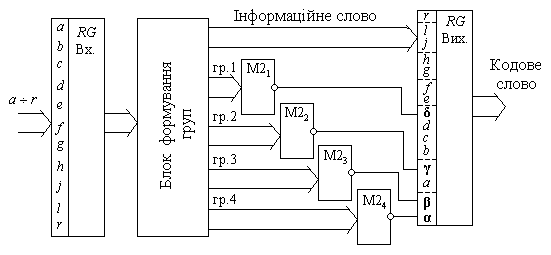
Рис.3.6.
На рис. 3.6 показана функціональна схема кодового перетворювача. За його допомогою семирозряднi сформовані групи інформаційного кодового слова подаються на схеми контролю парності M21 – M24. Результати контролю кожної групи записуються в контрольний розряд відповідної групи, створюючи на вихідному регістрі кодове слово, що передавалося.
Відповідно до відображеного на рис. 3.5 принципу формування кодового слова, в блоці формування груп створюються групи контролю, які подають свої сигнали разом з контрольним розрядом на схеми контролю парності М2. Виходи блоків M21 – M24 створюють керуючий код К. Якщо при передачі кодового слова в одному з його розрядів з’явилась похибка (на рис. 3.5 приведений приклад появи похибки в 5-му розряді, звідки виходять лінії), то буде зафіксовано порушення парності одиниць в розрядах коригуючого коду, відповідних контрольним групам з розрядом похибки. В результаті коригуючий код вказуватиме на номер того розряду кодового слова, в якому з’явилась похибка. Так, на рис. 3.5 контрольний код 0101 вказує на 5-й розряд.
Для відновлення інформації в слові, що передавалося, необхідно в визначеному розряді проiнвертувати його значення. Схема, яка вирішує цю задачу, приводиться на рис. 3.7. Кодове слово, що приймається вхідним регістром, перетворюється в чотири восьмирозряднi кодові групи, які контролюються на парність одиниць восьмирозрядними блоками M21 – M24. Входи блоків контролю парності дешифруються, i, якщо в i-му розряді має місце похибка, то одиничний сигнал подається на i-й керований інвертор i змінює стан розряду інформаційного слова. При відсутності збоїв в передачі інформації одиничний сигнал з’являється на нульовому вході дешифратора.
Для цього при проектуванні кодового перетворювача необхідно закласти реалізацію ним допоміжної функції 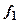 , яка задається як функція аргументів, значення якої співпадають із значеннями суми по модулю 2 решти функцій. Протифазна функція
, яка задається як функція аргументів, значення якої співпадають із значеннями суми по модулю 2 решти функцій. Протифазна функція 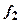 є схемою контролю парності всіх функціональних виходів перетворювача, окрім
є схемою контролю парності всіх функціональних виходів перетворювача, окрім 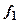 . Одиночна похибка в роботі як схеми перетворювача, так i схеми М2 змінить значення парності або
. Одиночна похибка в роботі як схеми перетворювача, так i схеми М2 змінить значення парності або 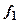 , або
, або 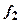 i буде зафіксована схемою контролю. Функція
i буде зафіксована схемою контролю. Функція 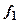 повинна синтезуватись з використанням вхідних змінних
повинна синтезуватись з використанням вхідних змінних 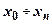 . Якщо ж використати для її побудови вихідні значення
. Якщо ж використати для її побудови вихідні значення 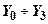 , то можливі похибки можуть змінити одночасно як
, то можливі похибки можуть змінити одночасно як 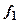 , так i
, так i 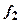 i не будуть виявлені. Вказану особливість необхідно враховувати при розробці схем контролю більш складних перетворювачів, в яких декілька різних виходів можуть мати загальні схемиi, відповідно, загальні збої, які потім не можуть бути виявлені схемами типу М2.
i не будуть виявлені. Вказану особливість необхідно враховувати при розробці схем контролю більш складних перетворювачів, в яких декілька різних виходів можуть мати загальні схемиi, відповідно, загальні збої, які потім не можуть бути виявлені схемами типу М2.
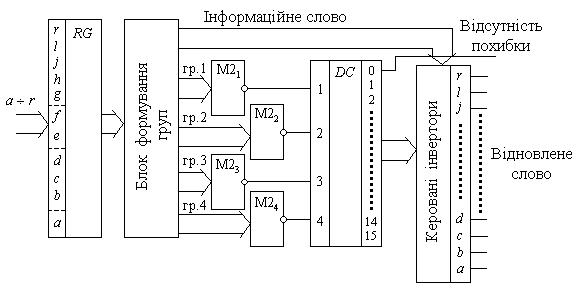
Рис.3.7.
Коди Хемiнга використовуються там, де вимоги до точності передачі даних досить високі.
Дата добавления: 2016-09-26; просмотров: 4412;











