Коди з виявленням і корекцією помилок

Зображення логічних функцій у вигляді n-вимірного кубу відкриває велику можливості не тільки в задачах мінімізації, а також в інших напрямках цифрової схемотехніки. Така геометрична інтерпретація надає можливість по-іншому бачити можливості різних кодів. Наприклад, представлення коду Грея у вигляді 3-вимірного куба має ту особливість, що код кожної сусідньої вершини відрізняється лише в одному біті (рис. 3.1).

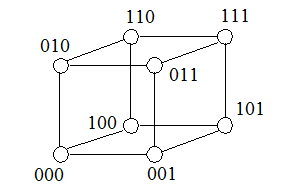
Рис.3.1.

Важливим моментом такої геометричної інтерпретації є відстань між двома n-бітними словами, тобто кількість біт, по яких два слова або дві вершини відрізняються між собою. З точки зору n-кубу – це мінімальна довжина шляху, який необхідно пройти (по ребрах кубу) від однієї вершини до іншої. Це, фактично, правило, за яким розраховується кодова відстань. Інше правило розрахунку кодової відстані полягає у знаходженні суми за модулем 2 між двома кодами, які приписані вершинам кубу. Після цього підраховується кількість одиниць в отриманій сумі.

Приклад 3.1. Знайти кодову відстань між двома вершинами n-вимірного кубу, що описуються наступними кодовими комбінаціями: А₁ = 10010; А₂ = 10111.

Розв’язання. Знаходимо суму за модулем 2:

А₁ Å А₂ = 00101.

Кодова відстань d = 2.

Поняття кодової відстані має суттєве значення при розв’язанні задач побудови кодів з виявленням помилок при передачі інформації. Структури n-кубу широко використовуються при побудові мультикомп’ютерних і мультипроцесорних обчислювальних систем.

Будь-який n-куб, подібно до таблиці станів, може розглядатись як поєднання більш простих однотипних структур. Така властивість витікає з таблиць відповідності більшості кодів. Наприклад, двійкові коди десяткових чисел 0 – 3 повторюються в кодах чисел 4 – 7 з різницею в старшому біті коду, що кодує числа в діапазоні 0 – 7.

Ідеологія побудови таких кодів полягає в тому, що при виникненні одиночної помилки в кодовому слові це слово вже не відноситься до множини кодових слів даного коду. Така ідеологія легко пояснюється на прикладі геометричної інтерпретації коду – n-вимірного кубу – з використанням поняття кодової відстані або кодового діапазону.

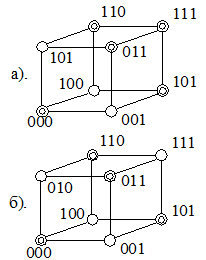
Рис.3.2.

На рис. 3.2, а приведений приклад коду (кодові слова позначені більш темними вершинами), в якому зміна в одному біті (наприклад, кодове слово 110 замінюється на 111), залишає це слово в наборі кодових слів, і тому така помилка при передачі інформації не може бути виявлена. Для коду, що представлений у вигляді n-кубу, зображеного на рис. 3.2, б, зміна одного біта будь-якого кодового слова призводить до того, що воно випадає зі словника коду, тому поява помилки в одному біті при передачі коду може бути одразу виявлена.

Виходячи з терміну “мінімальна відстань між двома кодовими словами n-кубу”, можна стверджувати, що в конкретному коді можуть біти виявлені всі одиночні помилки, якщо мінімальна відстань між будь-якими парами кодових слів дорівнює 2.

У загальному плані, якщо ми маємо шину передачі даних в n біт, то вона може забезпечувати передачу 2ⁿ кодових слів. Для того, щоб виявити одиночну помилку, необхідно мати лише один допоміжний біт, оскільки це надає можливість у n-вимірному кубі мати мінімальну відстань – 2. На практиці такий біт називається бітом парності, що пов’язано з особливостями схемотехніки.