Закони і тотожності алгебри логіки

Цифрові автомати без пам’яті (комбінаційні автомати)

Основні визначення

У практиці інженерної діяльності часто мають місце ситуації, при яких має значення не рівень сигналів, що поступають з відповідних датчиків, а лише наявність чи відсутність таких сигналів. Наприклад, у системах охоронної сигналізації необхідно знати, замкнені чи не замкнені двері або вікна в приміщенні, що охороняється. У системах автоматики часто необхідно знати, чи не перевершує кількість рідини в цистерні заданий рівень, чи не є тиск у котлі нижчим визначеної межі, чи не перевершує температура в приміщенні задану величину і т. п.

Схеми, що дають можливість розв’язувати поставлені задачі, можуть описуватись виразами типу: “лампочка на пульті охоронної сигналізації горить, якщо всі вікна замкнені (точніше, замкнено перше і друге і третє і… вікно)”. Або “лампочка не горить, якщо хоча б одне вікно відкрите (тобто може бути відкритим перше або друге або третє або перше і друге або...)”. Такі вирази називаються логічними.

При проектуванні подібних систем задаються відповідним рівнем напруги живлення, і наявність чи відсутність її дає можливість одержувати відповіді на поставлені питання. Оскільки рівень напруги може бути різним і задаватись прийнятою елементною базою, то з метою формалізації опису подібних схем приймаються деякі умови. Як приклад, високий рівень напруги приймається за “1”, низький – відповідно, за “0”. У такому разі приведені вище вирази можуть бути формалізовані: якщо контакти, що фіксують положення вікон, позначити як аргументи х₁ ,х₂ , …, х_n , які можуть приймати лише значення “1” або “0”, то напругу на лампочці можемо розглядати як функцію у, яка теж приймає одне з двох аналогічних значень.

Математичний апарат, що оперує з аргументами та функціями, які набувають тільки двох значень – “0” та “1” – називається двійковою (булевою) алгеброю або алгеброю логіки. Такий математичний апарат для розв’язання задач формальної логіки розробив ірландський математик Дж. Буль.

Логічні змінні (аргументи), як і змінні звичайної алгебри, позначаються літерами латинського алфавіту з різними індексами – наприклад, х₀ , х₁ , х₂ , х₃ , … Індекс при змінній може одночасно означати розряд двійкового числа.

Якщо змінна х_і набуває значення х_і = 1, то таке її значення називають істинним. Протилежнех_і = 0 називають хибним і умовно позначають 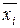, що означає заперечення істинного значення аргументу (в зарубіжній практиці операція заперечення позначається апострофом х' ). Два елементи булевої алгебри – подія істинна і подія хибна – називають її константами.

Булева функція позначається літерою у і є двійковою функцією двійкових аргументів. Умовне її позначення

у = f (x₁ , x₂ , ..., x_n).

Булева функція, яка залежить від n аргументів, називається n-вимірною і є повністю визначеною, якщо вказані значення її для всіх двійкових наборів значень її аргументів. Кількість таких наборів дорівнює 2ⁿ.Тобто, областю визначеності функції n змінних є сукупність дискретних точок n-вимірного простору, причому кожна з точок є комбінацією значень цих змінних (кодовою комбінацією). Оскільки можливі 2ⁿ різних комбінацій логічних змінних, то область визначення функції складається зі скінченої величини – 2ⁿ точок. Це, в свою чергу, означає, що кожна функція може бути задана таблицею значень, які вона приймає в точках її області визначеності.

Функція повністю визначена, якщо задані її значення в усіх точках області визначеності. Значення функції вибираються з множини “0” і “1”. Якщо ж значення функції не задано в одній або кількох точках, то вона є неповністю визначеною. Кодові комбінації, при яких функція невизначена, називаються факультативними. У практиці цифрової схемотехніки існує велика кількість неповністю визначених функцій. Довизначення їх, якщо це необхідно, забезпечується встановленням їх значень – “0” або “1” –довільним шляхом.

Усі можливі логічні функції n змінних можна створити за допомогою трьох основних операцій:

а) логічне заперечення (інверсія, операція НІ); позначається рискою над відповідною функцією або аргументом;

б) логічне додавання (диз’юнкція, операція АБО), яке позначається символами (V), (+);

в) логічне множення (кон’юнкція, операція І), яке позначається символами (Ù), (∙), (&). Для позначення еквівалентності логічних виразів використовується знак (=).

Запереченням (інверсією)називається такий зв’язок між аргументом х та функцією y,при якому у істинна тоді і тільки тоді, коли значення х хибне, і навпаки.

Логічним множенням (кон’юнкцією)декількох змінних називається така функція, яка істинна тоді і тільки тоді, коли одночасно істинні всі логічні змінні.

Логічним додаванням (диз’юнкцією)декількох змінних називається така функція, яка хибна тоді і тільки тоді, коли одночасно хибні всі додавані змінні.

Слід пам’ятати, що операція кон'юнкції є старшою операцією і виконується раніше диз’юнкції.

Прикладом найпростіших функцій є наступні:

; ; .

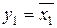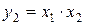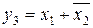Приклад 2.1. Записати вираз функції трьох змінних, яка приймає істинні значення при умові, що будь-яка пара змінних одночасно має істинні значення.

Розв’язання. Введемо умовні позначення змінних х₀ , х₁ , х₂ .

У загальному плані функція матиме вигляд:

у = f ( х₂ , х₁ , х₀ ).

Оскільки істинні значення функції визначаються будь-якою парою логічних змінних, тобто або х₀ і х₁ , або х₀ і х₂ , або х₁ і х₂ , то аналітична форма запису функції прийме вигляд:

у₁ = х₀ ∙ х₁ + х₀ ∙ х₂ + х₁ ∙ х₂ .

Функція може мати і дещо іншу форму запису, якщо враховувати, що при виконанні будь-якої з умов, що закладені в функцію, обмежень на значення третьої змінної не накладається.

Приклад 2.2. Формалізувати та записати у вигляді булевих функцій висловлення: лампочка охоронної сигналізації світиться, коли всі три двері приміщення зачинені.

Розв’язання. Позначимо логічні змінні х₁ , х₂ , х₃ істинними, якщо відповідні двері зачинені. В такому випадку істинне значення функції (“лампочка сигналізації світиться”) визначається за формулою:

у₂ = х₁ ∙ х₂ ∙ х₃ .

Приклад 2.3. Формалізувати та записати у вигляді булевих функцій висловлення: температурна сигналізація вмикається, коли хоча б один з двох датчиків зафіксує температуру 70°.

Розв’язання. Приймемо за істинне значення логічних змінних х₁ , х₂ показ датчика, що відповідає температурі 70°.

У такому випадку логічна функція має вигляд:

у₃ = х₁ + х₂ + х₁ ∙ х₂ .

Приклад 2.4. Змагання зі штанги судять три судді: головний, що знаходиться проти помосту, і два бокові. Якщо суддя вважає, що вага взята, він натискає кнопку, яка знаходиться на його столі. Для спортсмена вага вважається взятою, якщо загорається лампочка біля помосту. Умова загорання лампочки наступна: вона загорається, якщо головний і, як мінімум, один з бокових суддів натиснули кнопки на своїх столах. Формалізувати умову загорання лампочки.

Розв’язання. Приймемо за логічні змінні кнопки, що знаходяться на столах суддів: х₁ – кнопка головного судді; х₂ та x₃ – бокових. Приймемо за істинне значення натиснуту кнопку х_і = 1. Тоді умова загорання лампочки формально може бути записана в вигляді:

.

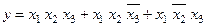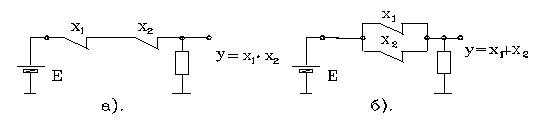
Рис.2.1.

Технічна реалізація булевих функцій, а, відповідно, і їх фізична інтерпретація добре ілюструється за допомогою контактних схем, в яких логічна змінна х_і відповідає замкненому контакту. Схеми, що ілюструють реалізацію операцій кон’юнкції та диз’юнкції, на­ведені відповідно на рис. 2.1, а, б.

Закони і тотожності алгебри логіки

В алгебрі логіки використовується ряд аксіом (тотожностей) та законів. Основними з них є наступні: переміщувальний (властивість комутативності); сполучний (властивість асоціатив­ності); розподільний (властивість дистрибутивності); інверсії (теорема де Моргана). Головні аксіоми та закони булевої алгебри наведені у табл. 2.1.

Таблиця 2.1.

Назва аксіоми чи закону	Вирази
Аксіоми (тотожності)	0 ∙ х = 0 1 + х = 1 0 + х = х x ∙ х = х х + х = х
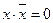
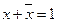
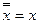
Закони комутативності	х1 + х2 = х2 + х1 х1 ∙ х2 = х2 ∙ х1
Закони асоціативності	х1 + х2 + х3 = х1 + (х2 + х3) = (х1 + х2) + х3 = = (х1 + х3) + х2   х1 ∙ х2 ∙ х3 = х1 ∙ (х2 ∙ х3) = = х2 × (х1 ∙ х3) = х3 × (х1 ∙ х2)
Закони дистрибутивності	х1 ∙ (х2 + х3) = х1 ∙ х2 + х1 ∙ х3   х1 + х2 ∙ х3 = (х1 + х2) ∙ (х1 + х3)
Закони інверсії (теорема де Моргана, принцип подвійності)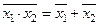
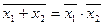
Закони поглинання	х1 + х1 ∙ х2 = х1   х1 ∙ (х1 + х2) = х1

Використовуючи наведені у табл. 2.1 закони та тотожності, які використовуються при перетворенні логічних функцій, можна створювати нові. Наприклад:

;

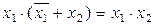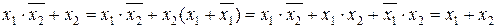
(у подальшому крапки, що відображають операцію логічного множення у формулах, для спрощення запису приводити не будемо).

Закони інверсії, які відображають властивість взаємного перетворення операцій логічного множення і додавання в алгебрі логіки, називають принципом подвійності.