Диаграмма динамической остойчивости
Наклоняющие моменты, действующие на судно, различаются по характеру их приложения к судну.
Например, перекачка жидкого груза на один борт сопровождается ростом кренящего момента настолько медленно, что скорость наклонения судна практически незаметна. В этом случае кренящий момент, измеряемый по его итоговому значению, считается приложенным статически.
Кренящий момент от сильного шквала ветра нарастает до полной величины за единицы или даже доли секунды. За такой период судно не успевает сколько-нибудь значительно изменить посадку и можно считать, что кренящий момент прикладывается к судну внезапно, т.е. уже в начальный момент имеет полную величину. Кренящий момент такого характера называется динамическим, а противодействие такому моменту – динамической остойчивостью.
Рассмотренные два случая являются предельными; реальные кренящие моменты по скорости нарастания нередко занимают промежуточное положение.
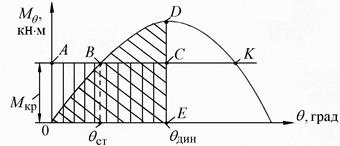
Рассмотрим процесс наклонения судна под действием динамического кренящего момента с использованием диаграммы восстанавливающих моментов (рис. 3.10). Допустим, к судну приложен постоянный динамический кренящий момент (Мкр = const).
|
Рис. 3.10. К определению динамического угла крена
Графиком действия такого момента на диаграмме будет горизонтальная прямая АК. На участке наклонения от А до В кренящий момент превышает восстанавливающий 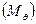 и судно будет крениться с положительным угловым ускорением. При этом массы, образующие массу судна будут перемещаться с положительным линейным ускорением и, как следствие, возникнут силы. Поскольку судно кренится, т.е. имеет место вращательное движение судна вокруг продольной оси, эти силы образуют инерционный момент, который «аккумулируется» судном. Инерционный момент «генерируется» на участке А-В «избыточным» кренящим моментом
и судно будет крениться с положительным угловым ускорением. При этом массы, образующие массу судна будут перемещаться с положительным линейным ускорением и, как следствие, возникнут силы. Поскольку судно кренится, т.е. имеет место вращательное движение судна вокруг продольной оси, эти силы образуют инерционный момент, который «аккумулируется» судном. Инерционный момент «генерируется» на участке А-В «избыточным» кренящим моментом 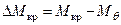 (рис. 3.10) и зависит от угла крена q.
(рис. 3.10) и зависит от угла крена q.
При значении угла qст(угол статического наклонения) кренящий (Мкр) и восстанавливающий (Мq) моменты равны.
На участке В-С нарастающий по величине Мq противодействует двум моментам – 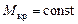 и инерционному моменту. При этом наклонение становится замедленным (с отрицательным угловым ускорением) и, в итоге, судно остановится при qдин (угол динамического наклонения).
и инерционному моменту. При этом наклонение становится замедленным (с отрицательным угловым ускорением) и, в итоге, судно остановится при qдин (угол динамического наклонения).
Затем, в силу того, что при qдин имеем 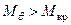 , судно с положительным угловым ускорением будет крениться до угла qст, при котором
, судно с положительным угловым ускорением будет крениться до угла qст, при котором 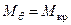 . По достижении qст вращательное движение судна в сторону начального положения (q = 0) продолжится с отрицательным ускорением; при этом Мкр будут противодействовать Мq и инерционный моменты. После остановки при q = 0 судно повторит описанный колебательный цикл.
. По достижении qст вращательное движение судна в сторону начального положения (q = 0) продолжится с отрицательным ускорением; при этом Мкр будут противодействовать Мq и инерционный моменты. После остановки при q = 0 судно повторит описанный колебательный цикл.
Представленная здесь динамика наклонений судна при приложении динамического кренящего момента является «идеализированной», т.к. не учитывает действия на судно сил, возникающих при его перемещении, в процессе наклонения, относительно воды и воздуха. В реальных условиях, при приложении к судну динамического 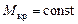 , оно будет совершать затухающие колебания и остановиться при угле θст (рис. 3.10).
, оно будет совершать затухающие колебания и остановиться при угле θст (рис. 3.10).
Наклонения судна при приложении к нему динамического момента 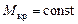 , как показано выше, представляют собой динамический процесс. При этом работа, совершаемая моментами Мкр и Мq в диапазоне углов
, как показано выше, представляют собой динамический процесс. При этом работа, совершаемая моментами Мкр и Мq в диапазоне углов 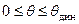 , взаимно «уравновешивается» (моменты выполняют одинаковую работу). Это условие можно записать в виде
, взаимно «уравновешивается» (моменты выполняют одинаковую работу). Это условие можно записать в виде
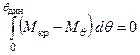 или или 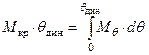 , ,
| (3.4) |
с учетом того, что 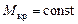 . Из (3.4) следует, что условием определения qдин является равенство площадей ОАСЕО и ОВДЕО (рис. 3.10), которые определяют работу моментов
. Из (3.4) следует, что условием определения qдин является равенство площадей ОАСЕО и ОВДЕО (рис. 3.10), которые определяют работу моментов 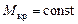 и Мq соответственно.
и Мq соответственно.
Здесь необходимо отметить, что с использованием диаграммы восстанавливающих моментов задача по определению угла динамического наклонения (qдин) при приложении к судну динамического момента 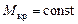 может быть решена графически путем нахождения положения на диаграмме вертикали (на рис. 3.10 вертикаль ДЕ), которая соответствует равенству площадей ВДСВ и ОАВО. Эти площади являются «избыточными» по отношению к площади ОВСЕО, которая определяет графически часть работы как момента Мкр так и Мq.
может быть решена графически путем нахождения положения на диаграмме вертикали (на рис. 3.10 вертикаль ДЕ), которая соответствует равенству площадей ВДСВ и ОАВО. Эти площади являются «избыточными» по отношению к площади ОВСЕО, которая определяет графически часть работы как момента Мкр так и Мq.
Представленный на рис. 3.10 метод определения qдин обладает наглядностью, но осложняется необходимостью подсчета площади. Другой метод решения задач, связанных с действием динамического кренящего момента, основан на использовании диаграммы динамической остойчивости.
Выражение (3.4) определяет работу 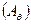 момента восстанавливающего
момента восстанавливающего
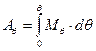 или или 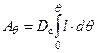 , ,
|
| где | Dс | – | вес судна при данной загрузке (Dс = const). |
С учетом последнего и, представив работу в виде 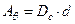 , можно записать
, можно записать
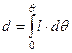 , ,
| (3.5) |
| где | d | – | называется плечо динамической остойчивости. |
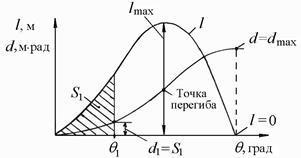
Геометрическая интерпретация зависимости (3.5) дана на рис. 3.11, из которого следует, что плечо динамической остойчивости (d1) при угле θ1, с учетом масштаба, равно площади (S1), ограниченной диаграммой статической остойчивости до этого же угла. В целом диаграмма динамической остойчивости есть интегральная кривая по отношению к диаграмме статической остойчивости.
Интегрирование по формуле (3.5) выполняется по углу, измеряемому в радианах; на диаграмме шкала θ дается в градусах.
|
Рис. 3.11. Диаграммы статической и динамической остойчивости
Из (3.5), с учетом характера зависимости l(q), следуют ряд соотношений диаграмм статической и динамической остойчивости:
· углу максимума диаграммы статической остойчивости соответствует точка перегиба диаграммы динамической остойчивости (рис. 3.11);
· углу заката диаграммы статической остойчивости соответствует максимум диаграммы динамической остойчивости;
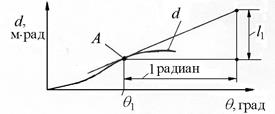
· если на диаграмме динамической остойчивости (рис. 3.12) провести при угле θ1 касательную к кривой d (А – точка касания) и отложить 1 радиан, получим плечо (в масштабе шкалы d) статической остойчивости (l1), соответствующее углу θ1.
|
Рис.3.12. К определению плеча статической остойчивости
по диаграмме динамической остойчивости
Определение плеч диаграммы динамической остойчивости для ее построения в судовых условиях может быть выполнено с использованием диаграммы статической остойчивости или универсальной диаграммы динамической остойчивости для судна.
Расчет плеч диаграммы динамической остойчивости выполняется в форме табл. 3.1.
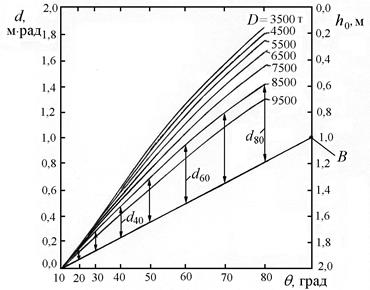
Универсальная диаграмма (рис. 3.13) позволяет без расчетов получить плечи диаграммы динамической остойчивости судна при данной его загрузке. Плечо d, определяемое по диаграмме, является результирующей величиной двух составляющих, т.е.
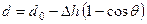 , ,
| (3.6) |
| где | d0 | – | плечо, соответствующее исходному (фиксированному) значению начальной метацентрической высоты 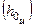 (на рис. 3.13 (на рис. 3.13 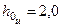 м), м),
|
поправка – 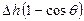 включает сомножитель
включает сомножитель 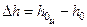 , где
, где 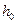 – расчетное значение начальной метацентрической высоты для судна.
– расчетное значение начальной метацентрической высоты для судна.
Зависимость (3.6) является интегральной по отношению к зависимости (3.3).
|
Рис. 3.13. Универсальная диаграмма динамической остойчивости
Плечи диаграммы динамической остойчивости для расчетных D и h0 определяются в виде вертикальных отрезков между соответствующей кривой D и лучом, проведенным из начала шкалы d в точку на шкале h0, соответствующую расчетному 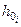 .
.
В качестве примера на рис. 3.13 показаны плечи диаграммы динамической остойчивости при D = 8500 т и h0 = 1,0 м (точка B). Значение плеча определяется в масштабе шкалы d.
Дата добавления: 2018-11-26; просмотров: 995;











