Лекция 16. Методы получения уравнений в пространстве состояний

Рассмотрим несколько примеров представления процессов в пространстве состояний.

Пример 1.

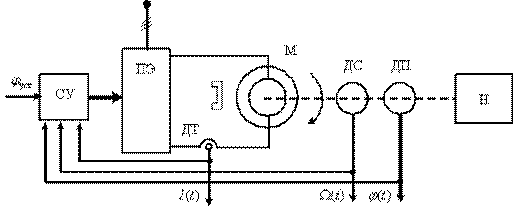
Рассмотрим в пространстве состояний процесс пуска электродвигателя (М) постоянного тока с постоянными магнитами, принципиальная схема установки показана на рис. 11. Пуск производится подключением с помощью контакта (К) напряжения 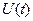, при этом в цепи будет протекать ток 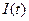и двигатель будет вращать вал с нагрузкой (Н) со скоростью 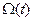, ток и скорость определяются с помощью датчиков соответственно ДТ и ДС.

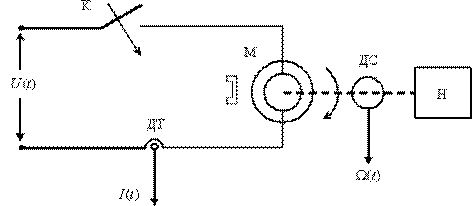
Рис. 11

Состояние двигателя в данном случае однозначно определяется током и скоростью двигателя, поэтому вектор состояния задается в следующем виде

.

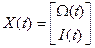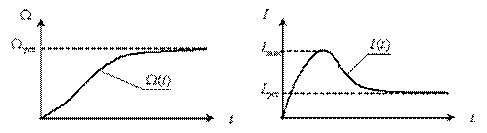
Вектор входа будет иметь только одну компоненту 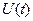. Графики изменения во времени переменных двигателя показаны на рис. 12.

Рис. 12

На рис. 12 введены обозначения: 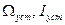– установившиеся значения соответственно скорости и тока, 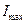– максимальное значение тока при пуске.

Сформируем двухмерное пространство (рис. 13) состояний двигателя с траекторией движения конца вектора состояния в процессе пуска, для этого откладываем проекции вектора, то есть ток и скорость, в одинаковые моменты времени.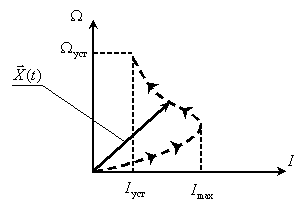
Рис. 13

Пример 2.

Рассмотрим в пространстве состояний процесс позиционирования, то есть перемещения вала в заданное положение 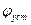, в автоматизированном электроприводе, показанном на рис. 14.

Рис. 14

В этом случае состояние двигателя и всей системы электропривода в целом определяют три переменных двигателя: ток 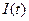, скорость 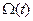и положение вала : .

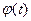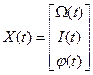Графики изменения во времени переменных двигателя показаны на рис. 15.

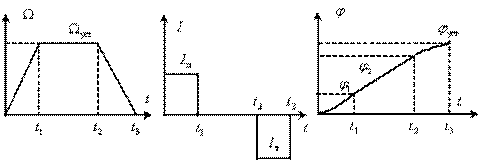
Рис. 15

Сформируем трехмерное пространство состояний электропривода (рис. 16) с траекторией движения конца вектора состояния в процессе позиционирования по временным графикам (рис. 15) изменения компонент вектора состояния.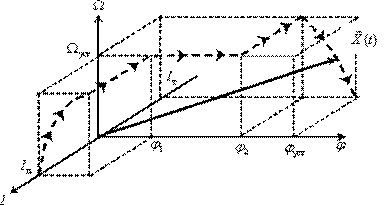
Рис. 16

Пример 3.

Рассмотрим получение математической модели многомерного объекта в виде уравнений состояния на примере двухмассовой упругой механической системы, показанной на рис. 17.

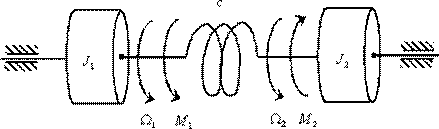
Рис. 17

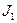Двухмассовая упругая система представляет собой механическую систему, состоящую из двух вращающихся масс с моментами инерции и . К каждой массе прикладывается извне момент ( 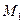и 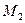), массы соединены валом, обладающим упругими свойствами ( 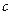), массы вращаются со скоростям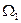и и .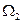

Система дифференциальных уравнений, описывающих систему, имеет вид

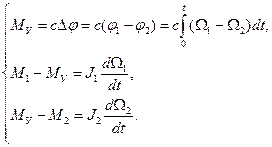(11)

где 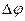– разность углов положения первой 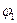и второй 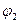масс.

Так как уравнения состояния (9) и выхода (10) имеют единый для всех линейных систем вид, поэтому, чтобы определить их для конкретной системы необходимо выполнить следующее:

– задать векторы состояния и входа, определив тем самым порядок системы и порядок вектора входа,

– определить матрицы параметров уравнений.

Состояние системы определяется тремя переменными 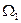, , 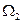, 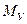поэтому вектор состояния имеет следующий вид

.

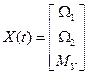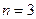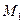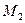Порядок системы . Заметим, что положение переменных в векторе состояния можно задать произвольно, но в дальнейшем изменять его нельзя. Вектор входа определяется сигналами, действующими на систему извне, а это – моменты и , поэтому вектор входа имеет вид

.

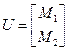Порядок вектора выхода 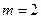. Здесь также порядок следования компонент может быть произвольным, но фиксированным в дальнейших операциях.

Преобразуем уравнения системы (11) к форме Коши

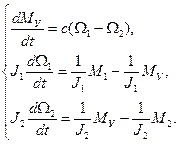
В общем виде уравнение состояния для системы третьего порядка с вектором входа второго порядка может быть записано следующим образом:

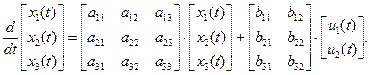
Раскрывая матричные скобки, получим

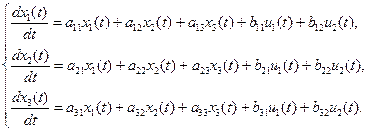(12)

Теперь можно сформулировать задачу следующего этапа. Необходимо привести систему (11) в виду (12), для этого следует:

– расположить уравнения в порядке следования компонент в векторе состояния,

– расположить слагаемые в правых частях слева на право в порядке следования сначала компонент вектора состояния, затем вектора входа,

– отсутствующие слагаемые заменяем произведениями переменных на нулевые коэффициенты.

В результате коэффициенты в правых частях при соответствующих компонентах векторов состояния и входа будут компонентами искомых матриц уравнения состояния.

Преобразуем систему (11) к виду (12), в результате получим

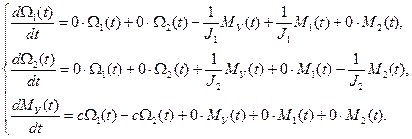(13)

В результате по коэффициентам слагаемых в правых частях (13) получим искомые матрицы параметров уравнения состояния:

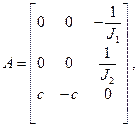
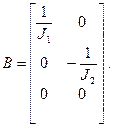
Уравнение состояния в развернутом виде

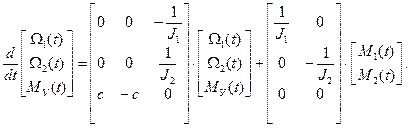
Вид уравнения выхода определяется тем, какие компоненты вектора состояния доступны для наблюдения. В электромеханических системах электроприводов, эквивалентом которых является упругая двухмассовая система, возможны три варианта систем (полагаем датчики безынерционными, а коэффициенты преобразования датчиков единичными):

1. Датчики скорости установлены на обеих массах. Тогда имеем следующее уравнение выхода

.

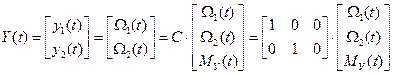2. Датчик скорости установлен на первой массе, уравнение выхода

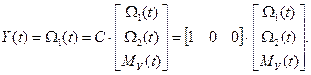
3. Датчик скорости установлен на второй массе, уравнение выхода

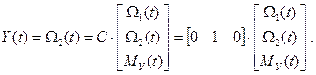
Уравнение состояния линейной стационарной системы (9) представляет собой матричную запись системы дифференциальных уравнений с постоянными коэффициентами в нормальной форме. Его решение, удовлетворяющее начальным условиям 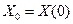, для вектора состояния и выходного вектора имеет вид:

;

.

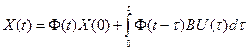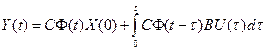Первые слагаемые соответствуют реакции, зависящей от начальных условий (свободное движение системы), а вторые слагаемые – реакции на входные воздействия (вынужденное движение).

Фундаментальная матрица 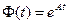называется переходной матрицей состояния системы. Она осуществляет линейное преобразование, которое переводит начальное состояние 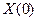системы в некоторое состояние для момента времени 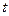(при нулевых входах), т. е. .

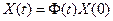Многомерная система характеризуется относительно ее входов и выходов матрицам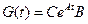и или 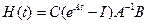, элементами которых являются соответственно импульсные 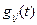или переходные 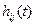характеристики для 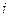-го выхода относительно 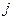-го входа (при нулевых состояниях на всех остальных входах).

Уравнения линейной стационарной системы

;

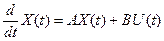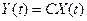
можно представить на основе преобразования Лапласа в операторной форме

; .

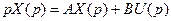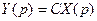Отсюда получаются решения для вектора состояния и выходного вектора

; .

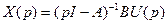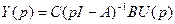Здесь матрица 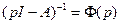является изображением переходной матрицы состояния системы .

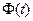Таким образом, переходная матрица состояния 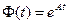может быть вычислена путем обращения матрицы 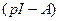и последующего перехода от 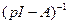к ее оригиналу. Для обращения матрицы подходит, например, алгоритм Фаддеева или любой другой способ обращения матрицы.

В результате имеем

,

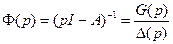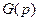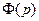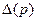где – присоединенная матрица для матрицы , а – характеристический многочлен матрицы 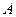, т. е. .

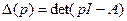Если все элементы 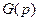имеют общие множители, то после сокращения на них 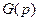переходит в приведенную присоединенную матрицу 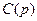, а 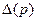– в минимальный многочлен.

Таким образом, при нулевых начальных условиях операторное выражение для выходного вектора принимает вид

.

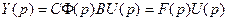Матрица 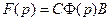называется передаточной матричной функцией. Так как изображение 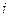-й выходной переменной 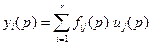, то элементы 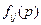матрицы 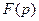можно рассматривать как скалярные передаточные функции от 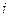-го входа к 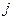-му выходу.

Зная 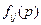, можно получить импульсную 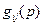и переходную 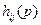характеристики. Для этого достаточно подставить в выражение 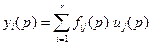вместо 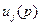соответственно изображения единичной импульсной функции 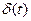, равное 1, и единичной ступенчатой функции, равное 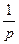. Тогда получим изображения для 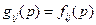и 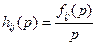. Для получения 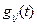и 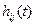следует перейти от их изображений к оригиналам на основе обратного преобразования Лапласа.