Глава 2. Математические модели в пространстве состояний

Лекция 15. Математические модели в пространстве состояний

Глава 2. Математические модели в пространстве состояний

Рассмотрим определение многомерной системы, используемое в теории управления. Многомерными системами называют системы управления, в которых имеются несколько, больше одной, управляемых переменных величин.

Одномерная система характеризуется тем, что контролируется (измеряется, регулируется) лишь одна переменная величина объекта управления. В этом случае, как система управления в целом, так и объект управления, представляются в виде математической модели, имеющей скалярные вход, выход и возмущающее воздействие. Для анализа и синтеза в таких системах используют математические модели в виде дифференциальных уравнений, передаточных функций, структурной схемы, частотных и временных характеристик, которые были рассмотрены ранее.

Общая тенденция развития промышленных устройств состоит в повышении качества и снижении затрат. При повышении качества управления приходится учитывать большее число возмущающих факторов и требуется управлять несколькими переменными объекта.

Обобщенная структура таких многомерных систем будет иметь вид, показанный на рис. 10.

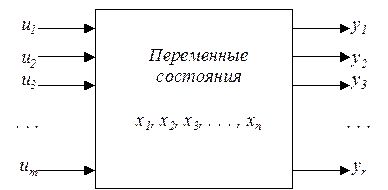
Рис. 10

На этом рисунке обозначены:

1) входные переменные 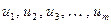, характеризующие внешние воздействия на входы системы;

2) переменные состояния 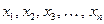– внутренние (промежуточные) переменные, совокупность которых полностью характеризует свойства системы;

3) выходные переменные 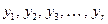, представляющие те реакции на внешние воздействия и те состояния системы, которые интересны для исследователя.

После упорядочения (нумерации) элементов этих множеств получаем соответственно три вектора: входной (задающий) вектор 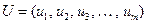, вектор состояний 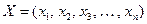и выходной вектор 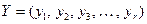. Сама система в общем виде представляется «черным ящиком» с 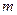входами и 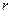выходами, с каждым из которых связана соответствующая переменная. Переменные состояния связаны с внутренними свойствами системы и поэтому указываются внутри «черного ящика». Собственно система, ее входы и выходы – это три взаимосвязанных объекта, которые в каждой конкретной ситуации определяются соответственно описанием системы (структура и свойства компонент или математическая модель системы), а также заданием множеств входных и выходных переменных.

В настоящее время в практике анализа и синтеза многомерных систем сложились два подхода к проблеме получения математической модели таких систем.

Суть первого подхода состоит в том, что многомерная система рассматривается, как многосвязная совокупность динамических звеньев и представляется в виде структурной схемы или ориентированного графа.

Суть второго подхода состоит в том, что при построении математических моделей используют векторно-матричное представление уравнений и структурных схем, описывающих объект управления или систему в целом.

В рамках этого подхода существует деление математических моделей на две группы.

Первую группу образуют математические модели в частотной области. Они базируются на операторной форме представления уравнений и использовании преобразования Лапласа. К таким моделям относятся:

– матричные структурные схемы,

– передаточные матрицы, которые иногда называют эквивалентными матрицами или матрицы «вход-выход».

Вторую группу образуют математические модели во временной области. Они базируются на векторно-матричной форме представления систем линейных дифференциальных уравнений первого порядка, широком использовании понятий и методов теории пространства состояний.

Основу математической модели многомерной системы во временной области составляет векторно-матричная форма записи системы дифференциальных уравнений первого порядка, которая носит название уравнения состояния. Уравнение состояния имеет вид

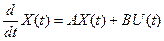, (9)

где 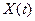– вектор состояния размерности 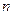, который включает в себя переменные объекта, однозначно определяющие его состояние

,

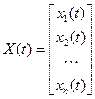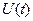– вектор управления или входа размерности 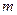, который включает в себя сигналы, действующие на систему извне,

,

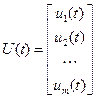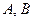– матрицы параметров, включающие в себя параметры системы, причем квадратная матрица 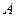размерностью 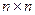называется матрицей системы, а матрица 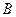размерностью 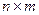называется матрицей управления:

, .

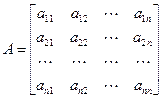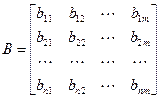Иногда уравнение состояния (9) записывают в развернутой форме

.

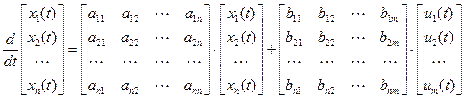Уравнение состояния полностью описывает объект управления, вектор состояния содержит переменные объекта, которые однозначно описывают его состояние.

Но в реальных системах многие компоненты не могут быть измерены или наблюдаемы с помощью датчиков. Эту ситуацию разрешает введение дополнительного уравнения выхода, которое определяет те переменные, которые доступны для наблюдения (на выходе системы),

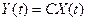, (10)

где 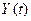– вектор выхода размерности 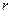, который содержит переменные объекта, доступные для наблюдения,

,

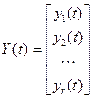матрица параметров 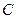размерностью 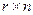называется матрицей выхода

.

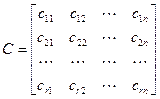Уравнение выхода (10) также можно записать в развернутой форме

.

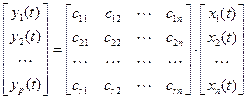Контрольные вопросы к лекции 15.

15-1. Какие системы управления называются многомерными?

15-2. Чем вызвана необходимость рассмотрения многомерных систем управления?

15-3. Как описывается многомерная система управления?

15-4. Что составляет основу математической модели многомерной системы во временной области?

15-5. Запишите в общем виде уравнение состояния системы.

15-6. Какая матрица в уравнении состояния системы называется матрицей системы?

15-7. Какая матрица в уравнении состояния системы называется матрицей управления?

15-8. Запишите в общем виде уравнение выхода системы.

15-9. Какая матрица в уравнении выхода называется матрицей выхода?