Глава 2. Динамическое представление сигналов
Во многих технических задачах, например при вычислении отклика физической системы на известное входное воздействие, требуется специфическая форма представления сигнала. Необходимо не только располагать информацией о мгновенном значении сигнала, но и знать его поведение на всей временной оси.
Способ получения таких моделей сигналов состоит в следующем. Реальный сигнал приближенно представляется суммой некоторых элементарных идеальных сигналов, возникающих в последовательные моменты времени. Если теперь устремить к нулю длительность отдельных элементарных сигналов, то в пределе будет получено точное представление исходного сигнала.
Широкое распространение получили два способа динамического представления. Согласно первому из них в качестве элементарных сигналов используют ступенчатые функции, возникающие через равные промежутки времени 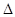 (рис. 3). Высота каждой ступеньки равна приращению сигнала на интервале времени (рис. 3). Высота каждой ступеньки равна приращению сигнала на интервале времени 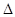 . .
| 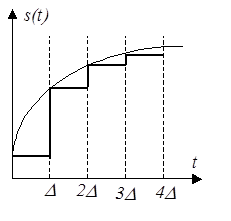
|
| Рис. 3 |
Рассмотрим свойства такого элементарного сигнала. Пусть дан сигнал, математическая модель которого задается системой:
 (1)
(1)
Такая функция описывает процесс перехода некоторого физического объекта из «нулевого» в «единичное» состояние. Переход совершается по линейному закону за время 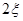 . Если параметр
. Если параметр  устремить к нулю, то в пределе переход из одного состояния в другое будет совершаться мгновенно. Математическая модель этого предельного сигнала получила название функции включения или функции Хевисайда:
устремить к нулю, то в пределе переход из одного состояния в другое будет совершаться мгновенно. Математическая модель этого предельного сигнала получила название функции включения или функции Хевисайда:
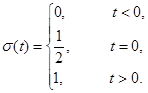 (2)
(2)
Рассмотрим некоторый сигнал 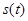 , причем для определенности положим, что , причем для определенности положим, что 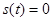 при при 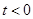 . Пусть . Пусть 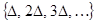 – последовательность моментов времени и – последовательность моментов времени и  – отвечающая им последовательность значений сигнала (рис. 4). Как видно из рисунка, текущее значение сигнала при любом – отвечающая им последовательность значений сигнала (рис. 4). Как видно из рисунка, текущее значение сигнала при любом 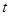 приближенно равно сумме ступенчатых функций: приближенно равно сумме ступенчатых функций:
| 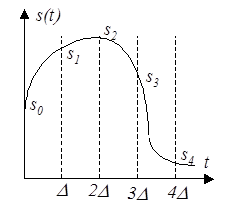
|
| Рис. 4 |
 .
.
Если теперь шаг 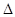 устремить к нулю, то дискретную переменную
устремить к нулю, то дискретную переменную 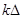 можно заменить непрерывной переменной
можно заменить непрерывной переменной 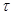 . При этом малые приращения
. При этом малые приращения 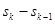 превращаются в дифференциалы и получается формула динамического представления произвольного сигнала посредством функций Хевисайда:
превращаются в дифференциалы и получается формула динамического представления произвольного сигнала посредством функций Хевисайда:
 . (3)
. (3)
| При использовании второго способа элементарными сигналами служат прямоугольные импульсы. Эти импульсы непосредственно примыкают друг к другу и образуют последовательность, вписанную в кривую (рис. 5). Рассмотрим свойства такого элементарного сигнала. | 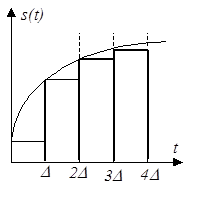
|
| Рис. 5 |
Математическая модель импульсного сигнала прямоугольной формы задается следующим образом:
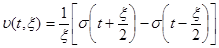 (4)
(4)
При любом выборе значения параметра  площадь этого импульса равна единице:
площадь этого импульса равна единице:
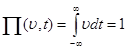 .
.
Пусть теперь величина  стремится к нулю. Импульс, сокращаясь по длительности, сохраняет свою площадь, поэтому высота его должна неограниченно возрастать. Предел последовательности таких функций при
стремится к нулю. Импульс, сокращаясь по длительности, сохраняет свою площадь, поэтому высота его должна неограниченно возрастать. Предел последовательности таких функций при  носит название дельта–функции или функции Дирака:
носит название дельта–функции или функции Дирака:
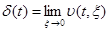 . (5)
. (5)
Возвращаясь к рис. 5, обозначим 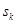 – значение сигнала на
– значение сигнала на  –м отсчете. Тогда элементарный импульс с номером
–м отсчете. Тогда элементарный импульс с номером  представляется следующим образом:
представляется следующим образом:
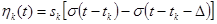 . (6)
. (6)
В соответствии с принципом динамического представления исходный сигнал 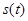 должен рассматриваться как сумма таких элементарных слагаемых:
должен рассматриваться как сумма таких элементарных слагаемых:
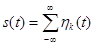 . (7)
. (7)
В этой сумме отличным от нуля будет только один член, отвечающий тому номеру  , который удовлетворяет неравенству
, который удовлетворяет неравенству 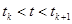 .
.
Если подставить (6) в (7), предварительно разделив и умножив на величину шага 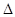 , то
, то
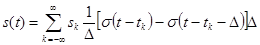 .
.
Переходя к пределу при 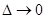 , необходимо заменить суммирование интегрированием по формальной переменной
, необходимо заменить суммирование интегрированием по формальной переменной 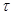 , дифференциал которой
, дифференциал которой 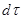 будет отвечать величине
будет отвечать величине 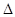 .
.
Поскольку  , получим искомую формулу динамического представления сигнала с помощью дельта–функции
, получим искомую формулу динамического представления сигнала с помощью дельта–функции
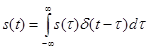 . (8)
. (8)
Итак, если непрерывную функцию умножить на дельта–функцию и произведение проинтегрировать по времени, то результат будет равен значению непрерывной функции в той точке, где сосредоточен 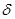 -импульс.
-импульс.
Дата добавления: 2016-09-06; просмотров: 2679;











