Глава 1. Основные определения
Многие задачи сводятся к рассмотрению совокупности объектов, существенные свойства которых описываются связями между ними. Например, глядя на карту автомобильных дорог, можно интересоваться только тем, имеется ли связь между некоторыми населенными пунктами, отвлекаясь от конфигурации и качества дорог, расстояний и других подробностей. При изучении электрических цепей на первый план может выступать характер соединений различных ее компонентов – резисторов, конденсаторов, источников и т. п. Органические молекулы образуют структуры, характерными свойствами которых являются связи между атомами. Интерес могут представлять различные связи и отношения между людьми, событиями, состояниями и вообще между любыми объектами.
В подобных случаях удобно рассматриваемые объекты изображать точками, называемыми вершинами, а связи между ними – линиями (произвольной конфигурации), называемыми ребрами. Множество вершин 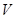 , связи между которыми определены множеством ребер
, связи между которыми определены множеством ребер 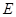 , называют графом и обозначают
, называют графом и обозначают 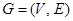 .
.
Теория графов располагает мощным аппаратом решения прикладных задач из самых различных областей науки и техники. Сюда относятся, например, анализ и синтез цепей и систем, проектирование каналов связи и исследование процессов передачи информации, построение контактных схем и исследование конечных автоматов, сетевое планирование и управление, исследование операций, выбор оптимальных маршрутов и потоков в сетях, моделирование жизнедеятельности и нервной системы живых организмов, исследование случайных процессов и многие другие задачи. Теория графов тесно связана с такими разделами математики, как теория множеств, теория матриц, математическая логика и теория вероятностей. Во всех этих разделах графы применяют для представления различных математических объектов, и в то же время сама теория графов широко использует аппарат родственных разделов математики.
Часто связи между объектами характеризуются вполне определенной ориентацией. Например, на некоторых улицах допускается только одностороннее автомобильное движение, в соединительных проводах электрической цепи задаются положительные направления токов, отношения между людьми могут определяться подчиненностью или старшинством. Ориентированные связи характеризуют переход системы из одного состояния в другое, результаты встреч между командами в спортивных состязаниях, различные отношения между числами (неравенство, делимость). Для указания направления связи между вершинами графа соответствующее ребро отмечается стрелкой. Ориентированное таким образом ребро называют дугой, а граф с ориентированными ребрами – ориентированным графом или короче орграфом (рис. 1).
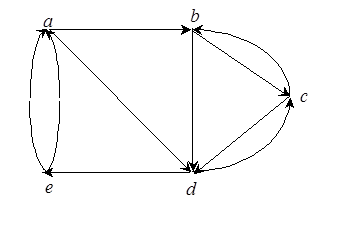
| 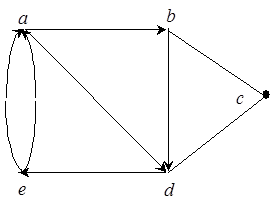
|
| Рис. 1 | Рис. 2 |
Если пара вершин соединяется двумя или большим числом дуг, то такие дуги называют параллельными. При этом две дуги, одинаково направленные по отношению к данной вершине, называют строго параллельными, а различно направленные – нестрого параллельными. Ясно, что нестрого параллельные дуги, отображающие ориентацию связи в обоих направлениях, по существу равноценны неориентированной связи и могут быть заменены ребром. Произведя такую замену в орграфе, придем к смешанному графу, который содержит ребра и дуги (рис. 2). Обратно, любой неориентированный или смешанный граф можно преобразовать в ориентированный заменой каждого ребра парой нестрого параллельных дуг.
Изменив направления всех дуг орграфа на противоположные, получаем орграф, обратный исходному. Если направления дуг орграфа не учитываются и каждая дуга рассматривается как неориентированное ребро, то он называется соотнесенным (неориентированным) графом.
Дальнейшее обобщение отображения связей между объектами с помощью графов состоит в приписывании ребрам и дугам некоторых количественных значений, качественных признаков или характерных свойств, называемых весами. В простейшем случае это может быть порядковая нумерация ребер и дуг, указывающая на очередность при их рассмотрении (приоритет или иерархия). Вес ребра или дуги может означать длину (пути сообщения), пропускную способность (линии связи), напряжение или ток (электрические цепи), количество набранных очков (турниры), валентность связей (химические формулы), количество рядов движения (автомобильные дороги), цвет проводника (монтажная схема электронного устройства), характер отношений между людьми (сын, брат, отец, подчиненный, учитель) и т. п. Вес можно приписывать не только ребрам и дугам, но и вершинам. Например, вершины, соответствующие населенным пунктам на карте автомобильных дорог, могут характеризоваться количеством мест в кемпингах, пропускной способностью станций техобслуживания. Вообще, вес вершины означает любую характеристику соответствующего ей объекта (атомный вес элемента в структурной формуле, цвет изображаемого вершиной предмета, возраст человека и т. п.).
Особое значение для моделирования физических систем приобрели взвешенные ориентированные графы, названные графами потоков сигналов или сигнальными графами. Вершины сигнального графа отождествляются с некоторыми переменными, характеризующими состояние системы, а вес каждой вершины означает функцию времени или некоторые величины, характеризующие соответствующую переменную (сигнал вершины). Дуги отображают связи между переменными, и вес каждой дуги представляет собой численное или функциональное отношение, характеризующее передачу сигнала от одной вершины к другой (передача дуги). Сигнальные графы находят широкое применение в теории цепей и систем, а также во многих других областях науки и техники.
Если множество вершин графа конечно, то он называется конечным графом. В математике рассматриваются и бесконечные графы, но мы заниматься ими не будем, так как в практических приложениях они встречаются редко. Конечный граф 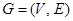 , содержащий
, содержащий 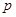 вершин и
вершин и 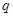 ребер, называется
ребер, называется 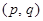 -гpaфoм.
-гpaфoм.
Пусть 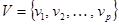 и
и 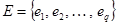 – соответственно множества вершин и ребер
– соответственно множества вершин и ребер 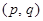 -графа. Каждое ребро
-графа. Каждое ребро 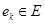 соединяет пару вершин
соединяет пару вершин 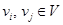 , являющихся его концами (граничными вершинами). Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. Ребра с одинаковыми граничными вершинами являются параллельными и называются кратными. В общем случае граф может содержать и изолированные вершины, которые не являются концами ребер и не связаны ни между собой, ни с другими вершинами. Например, для (5, 6)-графа на рис. 3
, являющихся его концами (граничными вершинами). Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Ребро, граничными вершинами которого является одна и та же вершина, называется петлей. Ребра с одинаковыми граничными вершинами являются параллельными и называются кратными. В общем случае граф может содержать и изолированные вершины, которые не являются концами ребер и не связаны ни между собой, ни с другими вершинами. Например, для (5, 6)-графа на рис. 3 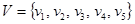 ;
; 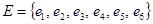 ; ребра
; ребра 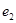 и
и 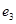 параллельны, ребро
параллельны, ребро 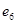 является петлей, а вершина
является петлей, а вершина 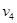 – изолированная вершина.
– изолированная вершина.
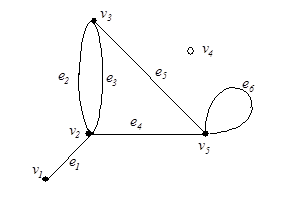
|
| Рис. 3 |
Число ребер, связанных с вершиной 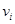 (петля учитывается дважды), называют степенью вершины и обозначают через
(петля учитывается дважды), называют степенью вершины и обозначают через 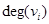 . Так, для графа на рис. 3
. Так, для графа на рис. 3 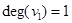 ,
, 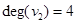 и т. д. Очевидно, степень изолированной вершины равна нулю (
и т. д. Очевидно, степень изолированной вершины равна нулю ( 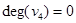 ). Вершина степени единицы называется концевой или висячей вершиной (
). Вершина степени единицы называется концевой или висячей вершиной ( 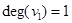 ). Легко показать, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно. В орграфе различают положительные
). Легко показать, что в любом графе сумма степеней всех вершин равна удвоенному числу ребер, а число вершин нечетной степени всегда четно. В орграфе различают положительные 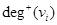 и отрицательные
и отрицательные 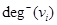 степени вершин, которые равны соответственно числу исходящих из
степени вершин, которые равны соответственно числу исходящих из 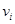 и заходящих в
и заходящих в 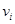 дуг. Например, для вершины
дуг. Например, для вершины 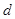 орграфа (рис. 1) имеем
орграфа (рис. 1) имеем 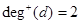 и
и 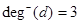 . Очевидно, суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны также числу всех дуг.
. Очевидно, суммы положительных и отрицательных степеней всех вершин орграфа равны между собой и равны также числу всех дуг.
Граф без петель и кратных ребер называют простым или обыкновенным. Граф без петель, но с кратными ребрами называют мультиграфом. Наиболее общий случай графа, когда допускаются петли и кратные ребра, называют псевдографом (рис. 3). Если граф не имеет ребер ( 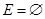 ), то все его вершины изолированы (
), то все его вершины изолированы ( 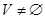 ), и он называется пустым или нуль-графом.
), и он называется пустым или нуль-графом.
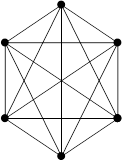
Простой граф, в котором любые две вершины соединены ребром, называется полным. На рис. 4 приведен пример полного графа с шестью вершинами. Если полный граф имеет 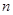 вершин, то число ребер этого графа определяется в соответствии с выражением вершин, то число ребер этого графа определяется в соответствии с выражением 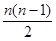 , т. е. с увеличением , т. е. с увеличением 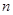 число ребер графа растет очень быстро. число ребер графа растет очень быстро.
| 
|
| Рис. 4 |
Если множество вершин 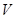 простого графа допускает такое разбиение на два непересекающихся подмножества простого графа допускает такое разбиение на два непересекающихся подмножества 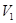 и и 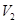 ( ( 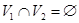 ), что не существует ребер, соединяющих вершины одного и того же подмножества, то он называется двудольным или биграфом (рис. 5). ), что не существует ребер, соединяющих вершины одного и того же подмножества, то он называется двудольным или биграфом (рис. 5).
| 
|
| Рис. 5 |
Ориентированный граф считается простым, если он не имеет строго параллельных дуг и петель. Граф, степени всех вершин которого одинаковы и равны 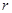 , называется однородным (регулярным)
, называется однородным (регулярным) 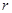 -й степени. Полный граф с
-й степени. Полный граф с 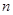 вершинами всегда однородный степени
вершинами всегда однородный степени 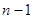 , а пустой граф – однородный степени 0. Граф третьей степени называют кубическим. Он обладает рядом интересных свойств и, в частности, всегда имеет четное число вершин.
, а пустой граф – однородный степени 0. Граф третьей степени называют кубическим. Он обладает рядом интересных свойств и, в частности, всегда имеет четное число вершин.
Две вершины 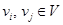 графа
графа 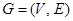 называются смежными, если они являются граничными вершинами ребра
называются смежными, если они являются граничными вершинами ребра 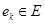 . Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин, т. е.
. Отношение смежности на множестве вершин графа можно определить, представив каждое ребро как пару смежных вершин, т. е. 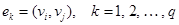 . Для неориентированных графов такие пары неупорядочены, так что
. Для неориентированных графов такие пары неупорядочены, так что 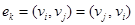 , а для орграфов – упорядочены, причем
, а для орграфов – упорядочены, причем 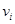 и
и 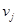 означают соответственно начальную и конечную вершины дуги
означают соответственно начальную и конечную вершины дуги 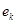 . Петля при вершине
. Петля при вершине 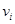 в обоих случаях представляется неупорядоченной парой
в обоих случаях представляется неупорядоченной парой 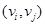 . Ясно, что множество вершин
. Ясно, что множество вершин 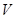 вместе с определенным на нем отношением смежности полностью определяет граф.
вместе с определенным на нем отношением смежности полностью определяет граф.
Граф можно представить также матрицей смежности. Строки и столбцы этой матрицы соответствуют вершинам графа, а ее 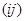 -й элемент равен числу кратных ребер, связывающих вершины
-й элемент равен числу кратных ребер, связывающих вершины 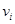 и
и 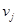 (или направленных от вершины
(или направленных от вершины 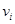 к вершине
к вершине 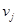 для орграфа). Элементы
для орграфа). Элементы 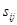 матрицы смежности
матрицы смежности 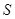 простого графа равны 0 или 1, причем все элементы главной диагонали нулевые.
простого графа равны 0 или 1, причем все элементы главной диагонали нулевые.
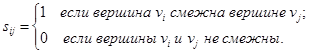
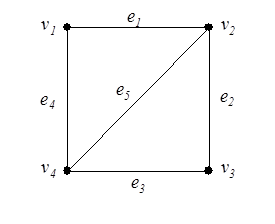
Например, для неориентированного графа, приведенного на рис. 6 и орграфа (рис. 7), имеем соответствующие матрицы смежности.
| 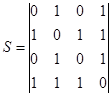
|
| Рис. 6 | |
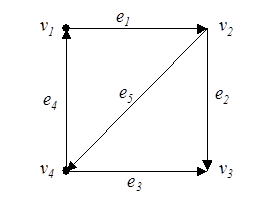
| 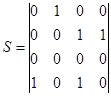
|
| Рис. 7 |
Матрица смежности неориентированного графа всегда симметрична, а орграфа – в общем случае несимметрична. Неориентированным ребрам соответствуют пары ненулевых элементов, симметричных относительно главной диагонали матрицы, дугам – ненулевые элементы матрицы, а петлям – ненулевые элементы главной диагонали. В столбцах и строках, соответствующих изолированным вершинам, все элементы равны нулю. Для взвешенного графа, не содержащего кратных ребер, можно обобщить матрицу смежности так, что каждый ее ненулевой элемент равняется весу соответствующего ребра или дуги. Обратно, любая квадратная матрица 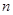 -го порядка может быть представлена орграфом с
-го порядка может быть представлена орграфом с 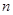 вершинами, дуги которого соединяют смежные вершины и имеют веса, равные соответствующим элементам матрицы. Если матрица симметрична, то она представима неориентированным графом.
вершинами, дуги которого соединяют смежные вершины и имеют веса, равные соответствующим элементам матрицы. Если матрица симметрична, то она представима неориентированным графом.
Если вершина 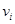 является концом ребра
является концом ребра 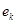 , то говорят, что они инцидентны, вершина
, то говорят, что они инцидентны, вершина 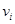 инцидентна ребру
инцидентна ребру 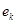 и ребро
и ребро 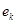 инцидентно вершине
инцидентно вершине 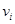 . В то время как смежность представляет собой отношение между однородными объектами (вершинами), инцидентность – это отношение между разнородными объектами (вершинами и ребрами). При рассмотрении орграфов различают положительную инцидентность (дуга исходит из вершины) и отрицательную инцидентность (дуга заходит в вершину). Рассматривая инцидентность вершин и ребер (
. В то время как смежность представляет собой отношение между однородными объектами (вершинами), инцидентность – это отношение между разнородными объектами (вершинами и ребрами). При рассмотрении орграфов различают положительную инцидентность (дуга исходит из вершины) и отрицательную инцидентность (дуга заходит в вершину). Рассматривая инцидентность вершин и ребер ( 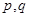 )-графа, можно представить его матрицей инцидентности
)-графа, можно представить его матрицей инцидентности 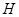 размера
размера 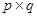 , строки которой соответствуют вершинам, а столбцы – ребрам. Для неориентированного графа элементы
, строки которой соответствуют вершинам, а столбцы – ребрам. Для неориентированного графа элементы 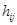 этой матрицы определяются по следующему правилу: элемент
этой матрицы определяются по следующему правилу: элемент 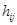 равен 1, если вершина
равен 1, если вершина 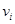 , инцидентна ребру
, инцидентна ребру 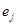 и равен нулю, если
и равен нулю, если 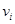 и
и 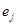 не инцидентны.
не инцидентны.
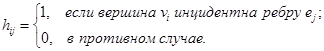
В случае орграфа ненулевой элемент 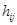 равен 1, если
равен 1, если 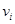 конечная вершина дуги
конечная вершина дуги 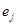 и равен –1, если
и равен –1, если 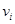 – начальная вершина дуги
– начальная вершина дуги 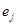 .
.
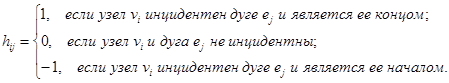
Например, для неориентированного графа, приведенного на рис. 8 и орграфа (рис. 9), имеем соответствующие матрицы инцидентности.
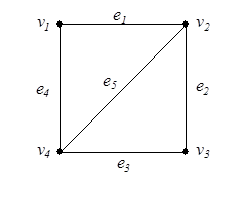
| 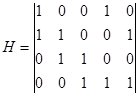
|
| Рис. 8 | |
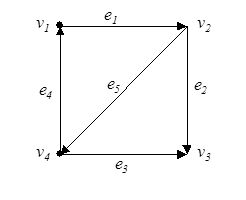
| 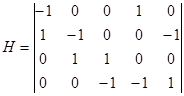
|
| Рис. 9 |
Каждый столбец матрицы инцидентности содержит обязательно два единичных элемента (для орграфа эти элементы всегда имеют различные знаки и равны соответственно 1 и –1). Количество единиц в строке равно степени соответствующей вершины (для орграфа количество положительных единиц определяет положительную степень, а количество отрицательных единиц – отрицательную степень). Нулевая строка соответствует изолированной вершине, а нулевой столбец – петле. Следует иметь в виду, что нулевой столбец матрицы инцидентности лишь указывает на наличие петли, но не содержит сведений о том, с какой вершиной эта петля связана (в практических приложениях это может быть несущественно).
На рис. 10 изображены три графа, которые с геометрической точки зрения совершенно различны (пересечение ребер, если оно не отмечено точкой, не является вершиной). Но по существу они различаются лишь начертанием, а отношения инцидентности (при соответствующем обозначении вершин и ребер) для них одинаковы. Графы, для которых сохраняется отношение инцидентности, называются изоморфными.

|
| Рис. 10 |
Ясно, что матрица инцидентности определяет граф без петель с точностью до изоморфизма. Обычно на ее основе можно изобразить различные в геометрическом отношении, но изоморфные между собой графы, каждый из которых называют геометрической реализацией. Графы, которые имеют одинаковые начертания и отличаются лишь нумерацией вершин и ребер, не будучи тождественными, являются изоморфными. Если существенные свойства графа не связаны со способом его изображения на плоскости или нумерацией вершин и ребер, то изоморфные графы, как правило, не различают между собой.
Нередко задачи на графах требуют выделения различных маршрутов, обладающих определенными свойствами и характеристиками. Маршрут длины 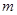 определяется как последовательность
определяется как последовательность 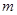 ребер графа (не обязательно различных) таких, что граничные вершины двух соседних ребер совпадают. Маршрут проходит и через все вершины, инцидентные входящим в него ребрам. Примерами маршрутов на графе рис. 3 могут служить последовательности
ребер графа (не обязательно различных) таких, что граничные вершины двух соседних ребер совпадают. Маршрут проходит и через все вершины, инцидентные входящим в него ребрам. Примерами маршрутов на графе рис. 3 могут служить последовательности 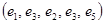 ,
, 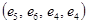 . Первый маршрут проходит через последовательность вершин
. Первый маршрут проходит через последовательность вершин 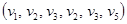 и соединяет вершины
и соединяет вершины 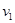 и
и 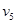 , а второй – через последовательность вершин
, а второй – через последовательность вершин 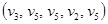 и соединяет вершины
и соединяет вершины 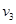 и
и 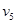 . Замкнутый маршрут приводит в ту же вершину, из которой он начался. Маршрут, все ребра которого различны, называется цепью, а маршрут, для которого различны все вершины, называется простой цепью. Замкнутая цепь называется циклом, а простая цепь – простым циклом. Так, на графе рис. 3
. Замкнутый маршрут приводит в ту же вершину, из которой он начался. Маршрут, все ребра которого различны, называется цепью, а маршрут, для которого различны все вершины, называется простой цепью. Замкнутая цепь называется циклом, а простая цепь – простым циклом. Так, на графе рис. 3 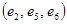 – цепь,
– цепь, 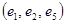 – простая цепь,
– простая цепь, 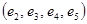 – цикл,
– цикл, 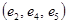 – простой цикл.
– простой цикл.
Цикл, который содержит все ребра графа, называется эйлеровым циклом, а граф, в котором имеется такой цикл, называется эйлеровым графом. Критерий существования эйлерова цикла выражается следующей теоремой: «Связный граф содержит эйлеров цикл тогда и только тогда, когда все его вершины имеют четную степень».
Простой цикл, который проходит через все вершины графа, называют гамильтоновым. Принципиальное отличие гамильтонова цикла от эйлерова цикла состоит в следующем: в эйлеровых циклах нужно пройти ровно один раз по всем ребрам графа, а в гамильтоновых циклах нужно пройти ровно один раз по всем вершинам графа. Если критерий существования эйлерового цикла очень прост (необходимо, чтобы степени всех вершин были четными), то для гамильтоновых циклов никакого общего правила не найдено.
Ориентированные маршруты на орграфе определяются аналогично с той разницей, что начальная вершина каждой последующей дуги маршрута должна совпадать с конечной вершиной предыдущей дуги. Иначе говоря, движение по маршруту допускается только в направлениях, указанных стрелками. Маршрут, не содержащий повторяющихся дуг, называется путем, а не содержащий повторяющихся вершин – простым путем. Замкнутый путь называется контуром, а простой замкнутый путь – простым контуром. Граф (орграф) называется циклическим (контурным), если он содержит хотя бы один цикл (контур), в противном случае он называется ациклическим (бесконтурным). Понятия цепи и цикла применимы и к ориентированным графам. При этом направления дуг не учитываются, т. е. по существу вместо орграфа рассматривают неориентированный соотнесенный ему граф.
Для графа 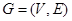 (рис. 11) граф
(рис. 11) граф 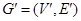 (рис. 12) является частью графа, если
(рис. 12) является частью графа, если 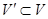 и
и 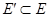 , т. е. граф содержит все вершины и ребра любой его части.
, т. е. граф содержит все вершины и ребра любой его части.
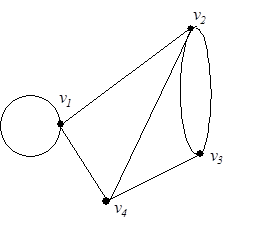
| 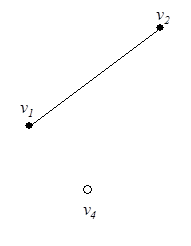
|
| Рис. 11 | Рис. 12 |
Часть, которая, наряду с некоторым подмножеством ребер графа, содержит и все инцидентные им вершины, называется подграфом (рис. 13). Часть, которая наряду с некоторым подмножеством ребер графа, содержит все вершины графа ( 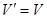 ,
, 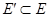 ), называется суграфом (рис. 14).
), называется суграфом (рис. 14).

| 
|
| Рис. 13 | Рис. 14 |
Исходный граф по отношению к его подграфу называют надграфом, а по отношению к суграфу – сверхграфом. Совокупность всех ребер графа, не принадлежащих его подграфу (вместе с инцидентными вершинами), образует дополнение подграфа. Говорят, что подграфы 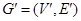 и
и 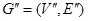 разделены ребрами, если они не имеют общих ребер (
разделены ребрами, если они не имеют общих ребер ( 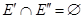 ) и разделены вершинами, если у них нет общих вершин (
) и разделены вершинами, если у них нет общих вершин ( 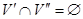 ).
).
Две вершины графа называют связанными, если существует маршрут, соединяющий эти вершины. Граф, любая пара вершин которого связана, называют связным графом.
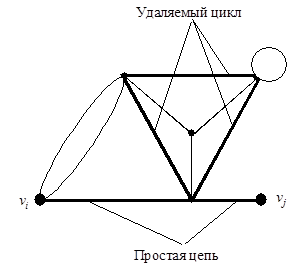
Очевидно, в связном графе между любыми двумя вершинами существует простая цепь, так как из связывающего их маршрута всегда можно удалить циклический участок, проходящий через некоторую вершину более одного раза (рис. 15, где маршрут между вершинами 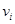 и и 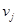 изображен жирными линиями). изображен жирными линиями).
| 
|
| Рис. 15 |
Если граф не связный, то множество его вершин можно единственным образом разделить на непересекающиеся подмножества, каждое из которых содержит все связанные между собой вершины и вместе с инцидентными им ребрами образует связный подграф.
Таким образом, несвязный граф представляет собой совокупность отдельных частей (подграфов), называемых компонентами.
На рис. 16 показан граф, состоящий из трех ( 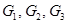 ) компонент (изолированная вершина считается компонентой). ) компонент (изолированная вершина считается компонентой).
| 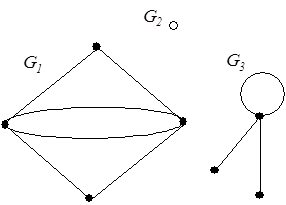
|
| Рис. 16 |
Часто отношение связности усложняется дополнительными условиями. Граф называют циклически связным, если любые две различные вершины содержатся в цикле (например, граф на рис. 11 циклически связный, а граф на рис. 15 – нет, так как вершина 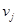 не содержится ни в каком цикле с другими вершинами). Граф называют
не содержится ни в каком цикле с другими вершинами). Граф называют 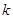 -связным, если любая пара различных вершин связана, по крайней мере
-связным, если любая пара различных вершин связана, по крайней мере 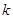 цепями, которые не имеют общих вершин (кроме начальной и конечной). Так, граф на рис. 11 двусвязный, а на рис. 15 – односвязный.
цепями, которые не имеют общих вершин (кроме начальной и конечной). Так, граф на рис. 11 двусвязный, а на рис. 15 – односвязный.
Связность ориентированных графов определяется так же, как и для неориентированных (без учета направлений дуг). Специфичным для орграфа (или смешанного графа) является понятие сильной связности. Орграф называют сильно связным, если для любой пары его вершин 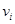 и
и 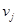 , существует путь из
, существует путь из 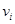 в
в 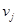 и из
и из 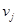 в
в 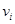 . Граф, представляющий план города с односторонним движением по некоторым улицам, должен быть сильно связным, так как в противном случае нашлись бы вершины (площади и перекрестки), между которыми нельзя было бы проехать по городу без нарушения правил движения.
. Граф, представляющий план города с односторонним движением по некоторым улицам, должен быть сильно связным, так как в противном случае нашлись бы вершины (площади и перекрестки), между которыми нельзя было бы проехать по городу без нарушения правил движения.
Связный граф может быть разделен на несвязные подграфы удалением из него некоторых вершин и ребер (при удалении вершин исключаются и все инцидентные им ребра, а при удалении ребер вершины сохраняются). Если существует такая вершина, удаление которой превращает связный граф (или компоненту несвязного графа) в несвязный, то она называется точкой сочленения (рис. 17). Ребро с такими же свойствами называется мостом (рис. 18). Ясно, что при наличии моста в графе имеется, по крайней мере, две точки сочленения.
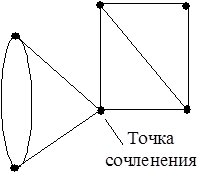
| 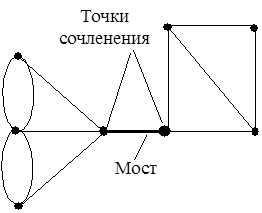
| |
| Рис. 17 | Рис. 18 |
Граф называется неразделимым, если он связный и не имеет точек сочленения (например, граф на рис. 11 неразделим). Граф, имеющий хотя бы одну точку сочленения, является разделимым и называется сепарабельным. Он разбивается на блоки, каждый из которых представляет собой максимальный неразделимый подграф (на рис. 19 показаны блоки B1, B2, B3 графа рис. 18).
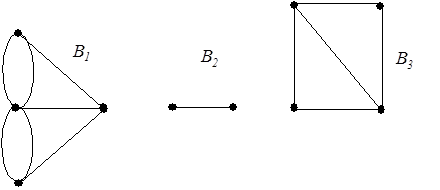
|
| Рис. 19 |
Каждое ребро графа, как и каждая вершина (за исключением точек сочленения), принадлежат только одному из его блоков. Более того, только одному блоку принадлежит и каждый простой цикл. Отсюда следует, что совокупность блоков графа представляет собой разбиение множеств ребер и простых циклов на непересекающиеся подмножества.
В ряде приложений теории графов блоки можно рассматривать как компоненты. Это обычно допустимо, когда связи блоков посредством точки сочленения несущественны или когда существенные свойства графа связаны только с его простыми циклами (контурами). В таких случаях можно рассматривать несвязный граф как связный разделимый граф, который образуется путем такого объединения компонент, чтобы каждая из них была блоком (это всегда можно сделать, объединив, например, по одной вершине каждого блока в точку сочленения). Подобные операции используются при рассмотрении графов электрических цепей.
Особый интерес представляют связные ациклические графы, называемые деревьями. Дерево на множестве 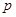 вершин всегда содержит
вершин всегда содержит 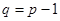 ребер, т. е. минимальное количество ребер, необходимое для того, чтобы граф был связным. Действительно, две вершины связываются одним ребром, и для связи каждой последующей вершины с предыдущими требуется ребро, следовательно, для связи
ребер, т. е. минимальное количество ребер, необходимое для того, чтобы граф был связным. Действительно, две вершины связываются одним ребром, и для связи каждой последующей вершины с предыдущими требуется ребро, следовательно, для связи 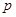 вершин необходимо и достаточно
вершин необходимо и достаточно 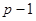 ребер. При добавлении в дерево ребра образуется цикл, а при удалении хотя бы одного ребра дерево распадается на компоненты, каждая из которой представляет собой также дерево или изолированную вершину. Несвязный граф, компоненты которого являются деревьями, называется лесом (лес из
ребер. При добавлении в дерево ребра образуется цикл, а при удалении хотя бы одного ребра дерево распадается на компоненты, каждая из которой представляет собой также дерево или изолированную вершину. Несвязный граф, компоненты которого являются деревьями, называется лесом (лес из 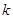 деревьев, содержащий
деревьев, содержащий 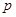 вершин, имеет в точности
вершин, имеет в точности 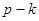 ребер). Сказанное иллюстрируется на примере дерева (рис. 20), которое превращается в циклический граф добавлением ребра (рис. 21) и распадается на лес из двух деревьев Т1 и Т2 при удалении ребра
ребер). Сказанное иллюстрируется на примере дерева (рис. 20), которое превращается в циклический граф добавлением ребра (рис. 21) и распадается на лес из двух деревьев Т1 и Т2 при удалении ребра 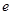 (рис. 22).
(рис. 22).
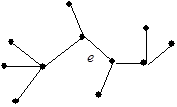
| 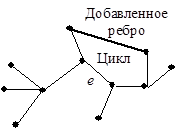
| 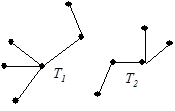
|
| Рис. 20 | Рис. 21 | Рис. 22 |
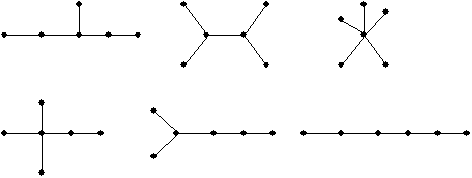
Обычно деревья считаются существенно различными, если они неизоморфны. На рис. 23 показаны все возможные различные деревья с шестью вершинами.
|
| Рис. 23 |
С увеличением числа вершин количество различных деревьев резко возрастает (например, при 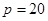 их насчитывается около миллиона). Среди различных деревьев выделяются два важных частных случая: последовательное дерево, представляющее собой простую цепь, и звездное дерево, в котором одна из вершин (центр) смежна со всеми остальными вершинами.
их насчитывается около миллиона). Среди различных деревьев выделяются два важных частных случая: последовательное дерево, представляющее собой простую цепь, и звездное дерево, в котором одна из вершин (центр) смежна со всеми остальными вершинами.
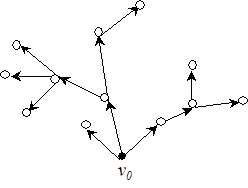
Рассматриваются также деревья с ориентированными ребрами (дугами). Ориентированное дерево называется прадеревом с корнем 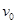 , если существует путь между вершиной
, если существует путь между вершиной  и любой другой его вершиной (рис. 24). Ясно, что прадерево имеет единственный корень.
и любой другой его вершиной (рис. 24). Ясно, что прадерево имеет единственный корень.
|
| Рис. 24 |
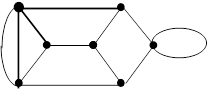
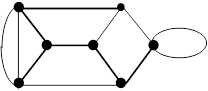
До сих пор рассматривались деревья как минимальные связные графы на множестве  вершин. Важное значение имеет и другая точка зрения, когда деревья или лес являются частями некоторого графа, т. е. образуются из его ребер. Любая связная совокупность ребер, не содержащая контуров, вместе с инцидентными им вершинами образует дерево графа (рис. 25а). Если такое дерево является суграфом (содержит все вершины графа), то оно называется покрывающим деревом или остовом (рис. 25б). Так как петля представляет собой простейший цикл, состоящий из единственного ребра, то она не может входить в состав любого дерева графа.
вершин. Важное значение имеет и другая точка зрения, когда деревья или лес являются частями некоторого графа, т. е. образуются из его ребер. Любая связная совокупность ребер, не содержащая контуров, вместе с инцидентными им вершинами образует дерево графа (рис. 25а). Если такое дерево является суграфом (содержит все вершины графа), то оно называется покрывающим деревом или остовом (рис. 25б). Так как петля представляет собой простейший цикл, состоящий из единственного ребра, то она не может входить в состав любого дерева графа.
| 
|
| а | б |
| Рис. 25 |
Ребра графа, которые принадлежат его дереву, называют ветвями. Если дерево покрывает граф, то множество ребер графа разбивается на два подмножества: подмножество ветвей и подмножество ребер дополнения дерева, называемых хордами. При этом связный 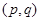 -граф содержит
-граф содержит 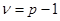 ветвей и
ветвей и 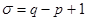 хорд. Если граф несвязный, то совокупность остовов
хорд. Если граф несвязный, то совокупность остовов 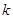 его компонент образует покрывающий лес. В этом случае
его компонент образует покрывающий лес. В этом случае 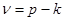 и
и 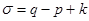 .
.
Деревья играют важную роль в различных прикладных задачах, когда, например, речь идет о связи каких-либо объектов минимальным числом каналов (линий связи, дорог, коммуникаций) с определенными свойствами. С помощью дерева определяется система координат при моделировании цепей и систем различной физической природы. Деревья используются в качестве моделей при рассмотрении иерархических систем объектов, структурных формул органических соединений и т. п.
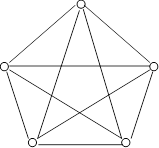
Граф называют плоским (планарным), если существует изоморфный ему граф (геометрическая реализация), который может быть изображен на плоскости без пересечения ребер. Например, хотя в одном из графов на рис. 10 ребра пересекаются, изоморфные ему графы, изображенные на том же рисунке, не имеют пересечений, следовательно, он плоский. На рис. 26 показаны два неплоских графа, играющие фундаментальную роль в теории планарности и называемые графами Понтрягина – Куратовского.
| 
|
| а | б |
| Рис. 26 |
Полный пятиугольник (рис. 26а) представляет собой простой неплоский граф с минимальным числом вершин (полный граф с четырьмя вершинами – плоский, а удаление из пятиугольника хотя бы одного ребра также превращает его в плоский граф). Двудольный граф (рис. 26б) является моделью известной задачи о трех домах и трех колодцах: можно ли проложить от домов к каждому колодцу дороги так, чтобы они не пересекались (враждующие соседи должны иметь возможность пользоваться всеми колодцами, но не хотят встречаться на дорогах)?
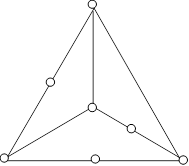
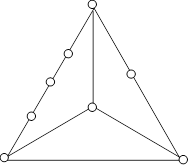
Свойства планарности не нарушаются, если некоторое ребро разбить на два введением новой вершины второй степени или заменить два ребра, инцидентные вершине второй степени, одним ребром, удалив эту вершину. Два графа называют гомеоморфными (изоморфными с точностью до вершин второй степени), если после удаления из них вершин второй степени и объединения инцидентных этим вершинам ребер, они оказываются изоморфными (рис. 27).
| 
|
| Рис. 27 |
Очевидно, граф, гомеоморфный плоскому графу, также плоский. Строго доказывается, что граф является плоским тогда и только тогда, когда он не содержит подграфа, гомеоморфного одному из графов Понтрягина – Куратовского.
Планарность является существенным свойством графов, которые моделируют коммуникации и связи между объектами на плоскости (дороги между населенными пунктами, водопроводные и газопроводные сети, линии передач электроэнергии, межсоединения на печатных платах электронных устройств и кристаллах интегральных схем).
Пусть на множестве 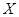 задано бинарное отношение
задано бинарное отношение 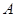 . Ему соответствует ориентированный граф, вершины которого отображают элементы из
. Ему соответствует ориентированный граф, вершины которого отображают элементы из 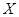 , а дуга (
, а дуга ( 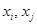 ), где
), где 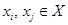 , существует тогда и только тогда, когда
, существует тогда и только тогда, когда 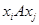 . Обратно, множество ориентированных дуг графа (без строго параллельных дуг), заданных упорядоченными парами (
. Обратно, множество ориентированных дуг графа (без строго параллельных дуг), заданных упорядоченными парами ( 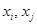 ), можно рассматривать как бинарное отношение на множестве
), можно рассматривать как бинарное отношение на множестве 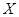 .
.
Если бинарное отношение 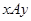 устанавливает связь между элементами
устанавливает связь между элементами 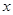 из множества
из множества 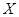 и элементами
и элементами 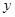 из множества
из множества 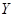 (
( 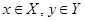 ), то граф такого отношения будет ориентированным биграфом.
), то граф такого отношения будет ориентированным биграфом.
Следует заметить, что в общем случае орграф представляет нечто большее, чем бинарное отношение. Любое бинарное отношение, определенное на некотором множестве, можно представить соответствующим орграфом, вершины которого соответствуют элементам этого множества. Однако орграф с параллельными дугами позволяет отражать более общие связи между объектами, чем бинарные отношения.
Дата добавления: 2016-09-06; просмотров: 2439;











